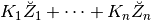Strateginių stalo žaidimų algoritmai¶
I had one item on my agenda today – not to lose.Šiandien mano dienotvarkėje buvo tik vienas punktas – nepralaimėti.Šachmatų čempionas Garis Kasparovas apie žaidimą šachmatais prieškompiuterinę programą Deep Junior
Smagu ir įdomu leisti laisvalaikį žaidžiant šaškėmis, šachmatais, Go ar net kryžiukais ir nuliukais, turint po ranka tik languotą popieriaus lapą. Smagiausia žaisti dviese, tačiau ne mažiau įdomu pabandyti sužaisti stalo žaidimą su kompiuteriu, kai vieno iš dviejų žaidėjų ėjimus atlieka programa. Galimas ir dar vienas žaidimo būdas: parašyti programas, atliekančias ėjimus, ir surengti programų turnyrą.
Kuo daugiau patirties turi žaidėjas ir kuo geresnę žaidimo strategiją jis sugalvos, tuo daugiau turi šansų laimėti. O kaip gi su programa, atliekančia žaidėjo ėjimus? Juk kiekvieno žaidimo taisyklės ir strategijos yra skirtingos. Ar gali būti kokie nors principai, bendri visiems žaidimams? Ar yra kas bendra tarp, pavyzdžiui, žaidimo šachmatais ir kryžiukais ir nuliukais? Pasirodo, yra! Visų strateginių stalo žaidimų algoritmai programuojami remiantis tais pačiais principais, kuriuos aprašysime šiame skyrelyje.
Strateginiai stalo žaidimai žaidžiami ant žaidimo lentos ar kitaip pažymėto žaidimo ploto su specialiais žaidimo komponentais (kauliukais, figūrėlėmis, kortelėmis). Žaidimą žaidžia du žaidėjai, kurie paeiliui atlieka ėjimus. Žaidimas yra baigtinis, t. y. jis būtinai baigsis po baigtinio ėjimų skaičiaus.
Strateginių žaidimų algoritmas – tai algoritmas, realizuojantis tam tikrą žaidimo strategiją, kuria remiantis parenkamas tolesnis ėjimas. Vartotojo sąsaja ir teisėjavimas neįeina į šią sąvoką. Tai suprantama – parašyti vartotojo sąsają šachmatų žaidimo programai galėtų daugelis išmanančių kompiuterinės grafikos pradmenis. Tačiau sukurti ir realizuoti strategiją, kuria žaidžiant pavyktų laimėti prieš rimtą varžovą, yra daug sudėtingesnis uždavinys.
Bendru atveju strateginių stalo žaidimų sąvoka gali būti platesnė, pavyzdžiui, žaidimą gali žaisti ne du, o daugiau žaidėjų, ėjimus jie gali atlikti ne tik paeiliui, bet ir praleisti ėjimą ar kelis kartus eiti iš eilės, remdamiesi konkrečiomis žaidimo taisyklėmis. Vaikams skirtuose žaidimuose ėjimus dažnai nulemia ir atsitiktinumas (pavyzdžiui, mesto kauliuko atsivertę taškai). Tačiau šiame skyrelyje nagrinėsime tik strateginius stalo žaidimus, paremtus klasikine stalo žaidimų samprata.
Trumpa stalo žaidimų istorija¶
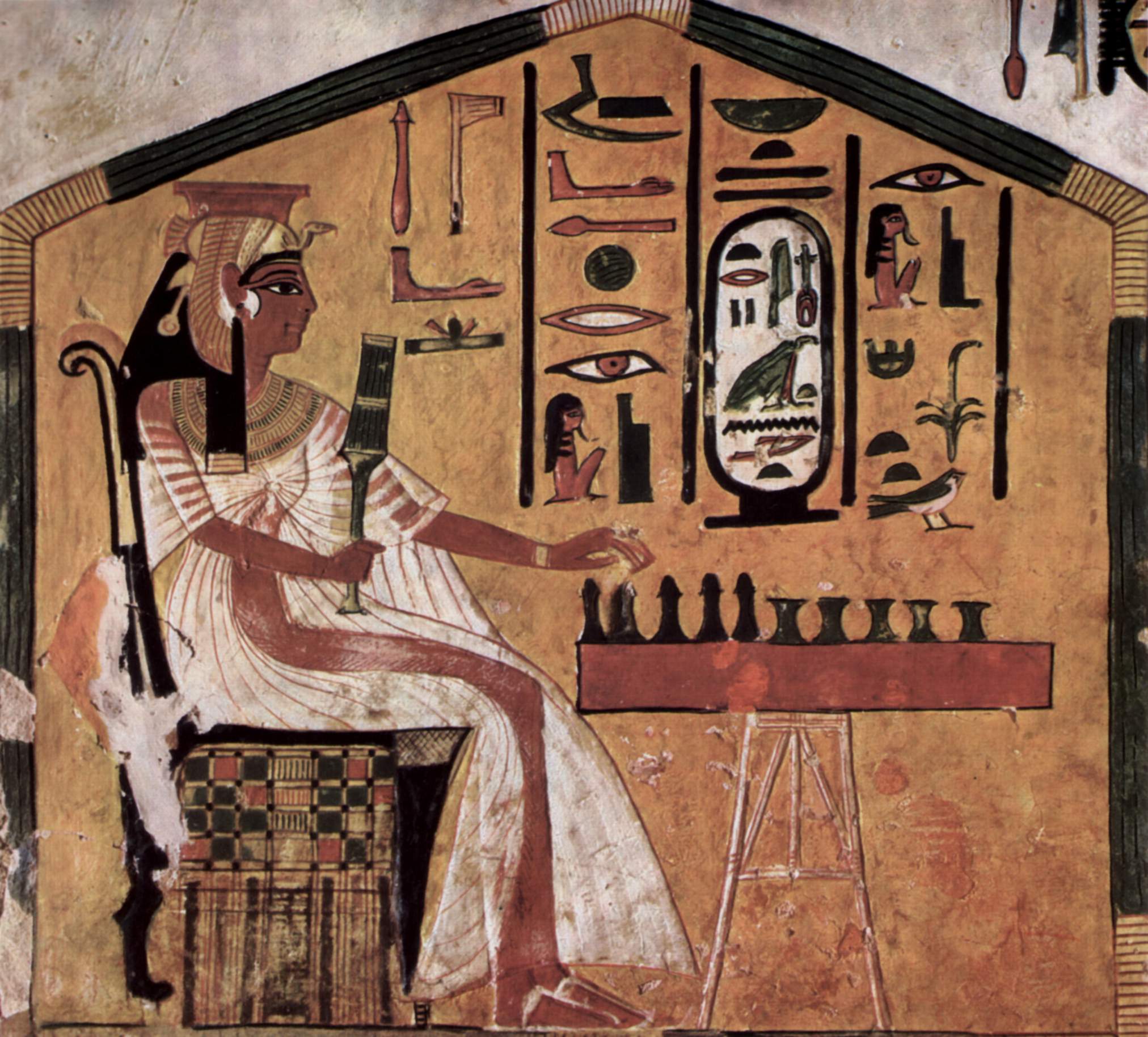
Fig. 77 Seneto žaidimas¶
Stalo žaidimai buvo populiarūs jau seovės civilizacijose. Seniausias
žinomas stalo žaidimas rastas senovės Egipte – žaidimas Senetas.
Piešiniai, kuriuose žaidžiamas šis žaidimas, buvo rasti ketvirto
tūkstantmečio prieš mūsų erą kapavietėse. Piešiniuose matyti,
kad Senetą galėjo žaisti du žaidėjai, kurie pradiniu momentu
turėjo nuo 5 iki 10 figūrėlių. Deja, tikslių šio žaidimo
taisyklių nėra išlikusių. Manoma, kad žaidimo lenta buvo
 dydžio, keletas jos langelių turėjo specialius
simbolius. Žaidėjas mesdavo keturias lazdeles (kiekviena kurių
turėjo dvi skirtingas puses) ir priklausomai nuo to, kas atsiversdavo,
atlikdavo ėjimą. Manoma, kad populiarus žaidimas Trik-trak (angl.
Backgammon) kilo iš Seneto.
dydžio, keletas jos langelių turėjo specialius
simbolius. Žaidėjas mesdavo keturias lazdeles (kiekviena kurių
turėjo dvi skirtingas puses) ir priklausomai nuo to, kas atsiversdavo,
atlikdavo ėjimą. Manoma, kad populiarus žaidimas Trik-trak (angl.
Backgammon) kilo iš Seneto.
Kitas senovės egiptiečių žaidimas yra Mehenas. Mehenas yra mitologinės būtybės vardas. Pirmosios nuorodos į šį žaidimą yra apie 3000 metus prieš mūsų erą. Žaidimo lenta priminė susirangiusią gyvatę (spiralės formos) ir buvo sudaryta iš stačiakampiukų. Manoma, kad žaidimas buvo žaidžiamas su liūtus ar liūtes primenančių figūrėlių rinkiniais iš 3–6 figūrėlių.

Fig. 78 Žaidžiamas stalo žaidimas Tabula¶
Viduramžiais išpopuliarėjo žaidimai kauliukais, kurie dažniausiai
buvo gaminami iš elnio ragų, taip pat kortomis. Buvo populiarūs ir
kiti stalo žaidimai. Jų figūrėlės dažnai būdavo pusrutulio
formos, gaminamos iš gintaro, kaulo, stiklo ar net arklio dantų. Vis
didesnį populiarumą ėmė įgauti šachmatai. Stalo žaidimai buvo
žaidžiami ne tik Azijoje, bet ir Europoje, Skandinavijoje. 1732
metais, keliaudamas po Laplandiją, žymus švedų botanikas Karlas
Linėjus (Carolus Linnaeus) aprašė žaidimą Tabula. Lapiai jį
žaidė  dydžio lentoje, o žaidimo figūrėles
vadino „Švedais“ ir „Rusais“.
dydžio lentoje, o žaidimo figūrėles
vadino „Švedais“ ir „Rusais“.
Stalo žaidimai labai išpopuliarėjo XX a. viduryje, ypač po II pasaulinio karo. O XX a. viduryje susidomėta ir strateginių žaidimų programavimu. Dar 1950 metais Klodas Elvudas Šenonas (Claude Elwood Shannon) paskelbė novatorišką darbą Kompiuterio programavimas žaisti šachmatais (angl. Programming a Computer for Playing Chess), kuriame aprašė, kaip skaičiavimo mašinai (ar kompiuteriui) galėtų būti parašyta programa, protingai žaidžianti šachmatais. Šenonas atkreipė dėmesį, kad teoriškai egzistuoja idealus sprendinys (t. y. ėjimų seka, kurią atlikdamas žaidėjas pasieks geriausią rezultatą), tačiau praktiškai jo rasti neįmanoma. Jis pateikė dvi euristika paremtas strategijas, kuriomis programuojant strateginius stalo žaidimus remiamasi iki šiol:
Generuoti visus įmanomus ėjimus iki tam tikro gylio (t. y. generuoti visus galimus pirmuosius ėjimus, visus galimus antruosius ėjimus ir t. t.), tuomet euristiškai įvertinti kiekvieną gautą situaciją lentoje, sudaryti žaidimo medį ir išrinkti geriausią ėjimą;
Generuoti tik perspektyvius ėjimus (žaidimo medžio šakas) ignoruojant ėjimus, kurie laikomi neperspektyviais.
Pirmoji šachmatais žaidžianti programa buvo parašyta ir įdiegta
1956 m. Taisyklės buvo supaprastintos, žaidžiama
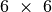 lentoje. Kompiuteris buvo tik 11 kHz dažnio ir
turėjo 600 žodžių atminties. Buvo realizuota A tipo Šenono
aprašyta strategija, generuojami 4 lygių ėjimai. Tam prireikdavo net
12 minučių. Ši programa įveikdavo tik silpnus žaidėjus.
lentoje. Kompiuteris buvo tik 11 kHz dažnio ir
turėjo 600 žodžių atminties. Buvo realizuota A tipo Šenono
aprašyta strategija, generuojami 4 lygių ėjimai. Tam prireikdavo net
12 minučių. Ši programa įveikdavo tik silpnus žaidėjus.
Po dvejų metų pirmą kartą buvo panaudotas Alfa-Beta atkirtimas, kuri leido padvigubinti analizuojamų ėjimų skaičių. Žaidimo programos buvo nuolat tobulinamos, pradėti rengti šachmatų programų turnyrai. Septintojo dešimtmečio viduryje (1975 m.) pradėta kurti Cray Blitz programa, kuri ilgą laiką buvo greičiausia šachmatais žaidžianti programa ir net septynerius metus buvo kompiuterių programų šachmatų čempionė.

Fig. 79 Garis Kasparovas žaidžia prieš Deep Junior programą, 2003 m.¶
1988 metais pirmą kartą kompiuterinė sistema Deep Thought, skirta žaisti šachmatais, nugalėjo didmeistrį Bentą Larseną (Bent Larsen). Programa, kurią kūrė studentai, jau sugebėdavo išanalizuoti iki 750 000 pozicijų per sekundę ir iki dešimties ėjimų į priekį. Ši sistema pralošė šachmatų čempionui Bobiui Fišeriui (Bobby Fischer). Vis dėlto, kuo toliau, tuo sunkiau didmeistriams sekėsi įveikti šachmatais žaidžiančias programas. Pirmoji kompiuterinė sistema, kuriai 1996 metais pralaimėjo partiją tuometinis pasaulio čempionas Garis Kasparovas, buvo Deep Blue. Tačiau tuomet turnyrą pasaulio čempionui vis tik pavyko laimėti. Deep blue buvo labai atnaujinta, neoficialiai netgi pervadinta į Deeper blue, ir 1997 metais Kasparovas jau pralaimėjo rezultatu 2,5:3,5. Tai buvo pirmas kartas, kai kompiuterinei sistemai pavyko įveikti pasaulio šachmatų čempioną matuojant žaidimo laiką įprastu būdu. 2003-iaisiais Gariui Kasparovui nepavyko įveikti ir Deep Junior programos – turnyras baigėsi lygiosiomis.
Šachmatai – tai tik vienas žaidimų, kuriam žaisti kuriamos kompiuterinės programos. Kasmet vyksta olimpiados 1, turnyrai, kuriuose tarpusavyje žaidžia programos ir kuriuose gali dalyvauti visi norintys.
Žaidimų medžiai, MiniMax paieška¶
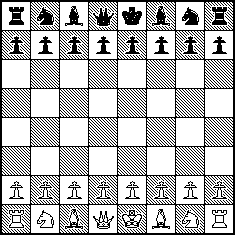
Fig. 80 Pradinė šachmatų žaidimo pozicija¶
Analizuodami strateginius stalo žaidimus sutarsime, kad abu varžovai žaidžia optimaliai, t. y. kiekvieną kartą renkasi patį palankiausią sau ėjimą.
Bet kuris stalo žaidimas prasideda nuo pradinės pozicijos.
Sutarsime, kad to paties žaidimo pradinė pozicija yra visada ta pati.
Pavyzdžiui, žaidžiant šachmatais, pradinę poziciją sudaro juodos
ir baltos figūros, išdėstytos tam tikra tvarka  lentoje, žaidžiant Go arba kryžiukais ir nuliukais, pradinę
poziciją sudaro tuščia lenta.
lentoje, žaidžiant Go arba kryžiukais ir nuliukais, pradinę
poziciją sudaro tuščia lenta.
Iš pradinės pozicijos pirmasis žaidėjas gali atlikti tam tikrus ėjimus. Visas šiais ėjimais gautas pozicijas vadinsime pirmojo lygio pozicijomis. Pozicijas, gautas atlikus vieną ėjimą iš pirmojo lygio pozicijų – antrojo lygio ir t. t.
Pavyzdžiui, žaidžiant kryžiukais ir nuliukais, pirmasis žaidėjas (jis būtinai žaidžia kryžiukais) gali atlikti 9 skirtingus pirmuosius ėjimus: padėti kryžiuką į bet kurį iš 9 langelių. Antrasis žaidėjas kiekvienu atveju gali pasirinkti vieną iš aštuonių ėjimų. Toliau pirmasis žaidėjas kiekvienu atveju gali atlikti septynis skirtingus ėjimus. Taip bus gaunamos trečiojo lygio pozicijos.
Analogiškai galima toliau generuoti ėjimus kol bus pasiektos baigiamosios žaidimo pozicijos, t. y. pozicijos, kai vienas žaidėjų laimi arba pasiekiamos lygiosios. Kryžiukų ir nuliukų atveju daugiausia gali būti 9 lygiai.
Iš žaidimo pozicijų sudaromas žaidimo medis, kurio viršūnės atitinka žaidimo pozicijas. Medžio šaknis atitiks pradinę žaidimo poziciją, jos antrinės viršūnės – visas pozicijas, kurias galima pasiekti vienu ėjimu iš startinės pozicijos (pirmojo lygio pozicijas) ir t. t.
Gali būti, kad tą pačią poziciją galima gauti atlikus kelias skirtingas ėjimų sekas. Tačiau konstruojant žaidimo medį į tai neatsižvelgiama: jei ta pati žaidimo pozicija buvo gauta dvejomis skirtingomis ėjimų sekomis, tai ji žymima dviem medžio viršūnėmis.
Visų pirmojo lygio pozicijų atstumas iki medžio šaknies bus lygus 1,
antrojo lygio pozicijų – 2, o  -ojo lygio pozicijų –
-ojo lygio pozicijų –
 .
.
Žaidimo pozicija vadinama laiminčia pozicija žaidėjui X, jei žaidėjas X galės taip parinkti tolimesnius savo ėjimus, kad jis laimės nepriklausomai nuo to, kaip žais jo varžovas arba jeigu tai yra baigiamoji žaidimo pozicija, kurioje laimi žaidėjas X. Atkreipsime dėmesį, kad žaidėjo X laiminčioje pozicijoje ėjimo teisė gali priklausyti bet kuriam iš dviejų žaidėjų.
Žaidimo pozicija vadinama pralaiminčia pozicija žaidėjui X, jei nesvarbu, kaip žaidėjas X žaistų, varžovas gali parinkti tokius tolimesnius savo ėjimus, kad jis (varžovas) būtinai laimės, arba jei tai yra baigiamoji žaidimo pozicija, kurioje žaidėjas X pralaimi. Žaidėjo X pralaiminčioje pozicijoje ėjimo teisė taip pat gali priklausyti bet kuriam iš dviejų žaidėjų.
Be abejo, kiekvienas žaidėjas stengiasi atlikti tokius ėjimus, kurie nuvestų į laiminčias žaidimo pozicijas.
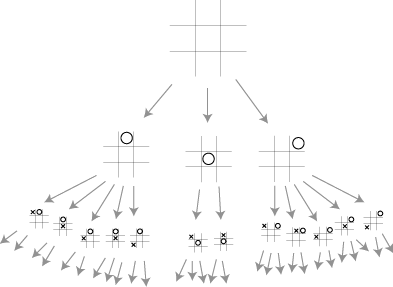
Fig. 81 Kryžiukų ir nuliukų žaidimo medžio pavyzdys; paveiksle parodyti tik du medžio lygiai; pateiktas nepilnas medis (atmestos simetriškos pozicijos)¶
Paanalizuokime konkretų uždavinį:
Lošimas disku 2: du žaidėjai paeiliui sukioja diską per vieną segmentą į kairę arba į dešinę. Žaidėjas, pasukęs diską, perskaito jo viršutiniame segmente atsiradusį skaičių
ir jį prideda prie sumos
(bendros abiems žaidėjams). Lošimo pradžioje
, o diskas atsisukęs ties skaičiumi 1. Lošimas baigiamas, kai
pasiekia arba viršija iš anksto sutartą skaičių
(pavyzdžiui,
). Laimi tas, kas atlieka paskutinį ėjimą, t. y. pasiekia arba viršija
.
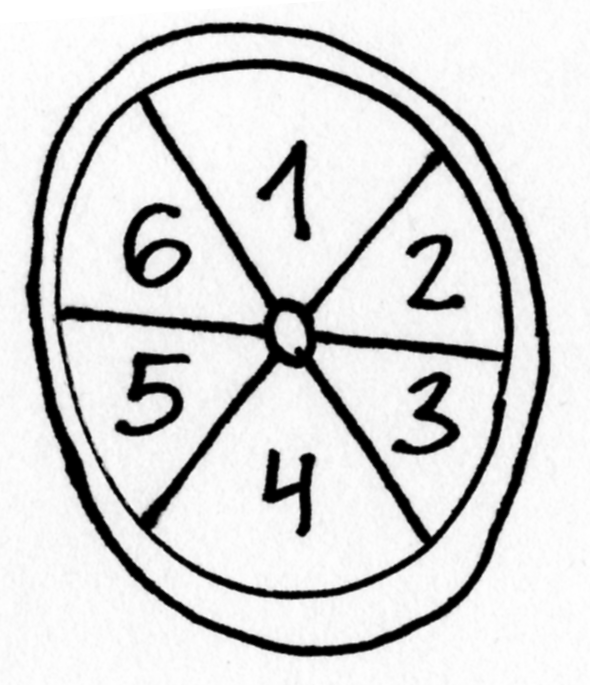
Fig. 82 Disko pozicija pradiniu momentu¶
Analizuosime žaidimą Lošimas disku, kai, pavyzdžiui, 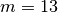 .
.
Fig. 83
paveiksle pateiktas pilnas žaidimo medis. Medis turi 9 lygius –
tai reiškia, kad galimi ne daugiau kaip 9 ėjimai. Bet kurią žaidimo
poziciją nusako pora 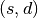 , kur
, kur  – bendra abiems
žaidėjams suma, o
– bendra abiems
žaidėjams suma, o 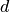 – skaičius, užrašytas ant į viršų
atsisukusio disko segmento. Visas medžio pozicijas bandysime skirstyti
į laiminčias ir pralaiminčias pirmajam žaidėjui (laiminti pirmojo
žaidėjo pozicija tuo pačiu yra pralaiminti antrojo žaidėjo pozicija
ir atvirkščiai).
– skaičius, užrašytas ant į viršų
atsisukusio disko segmento. Visas medžio pozicijas bandysime skirstyti
į laiminčias ir pralaiminčias pirmajam žaidėjui (laiminti pirmojo
žaidėjo pozicija tuo pačiu yra pralaiminti antrojo žaidėjo pozicija
ir atvirkščiai).
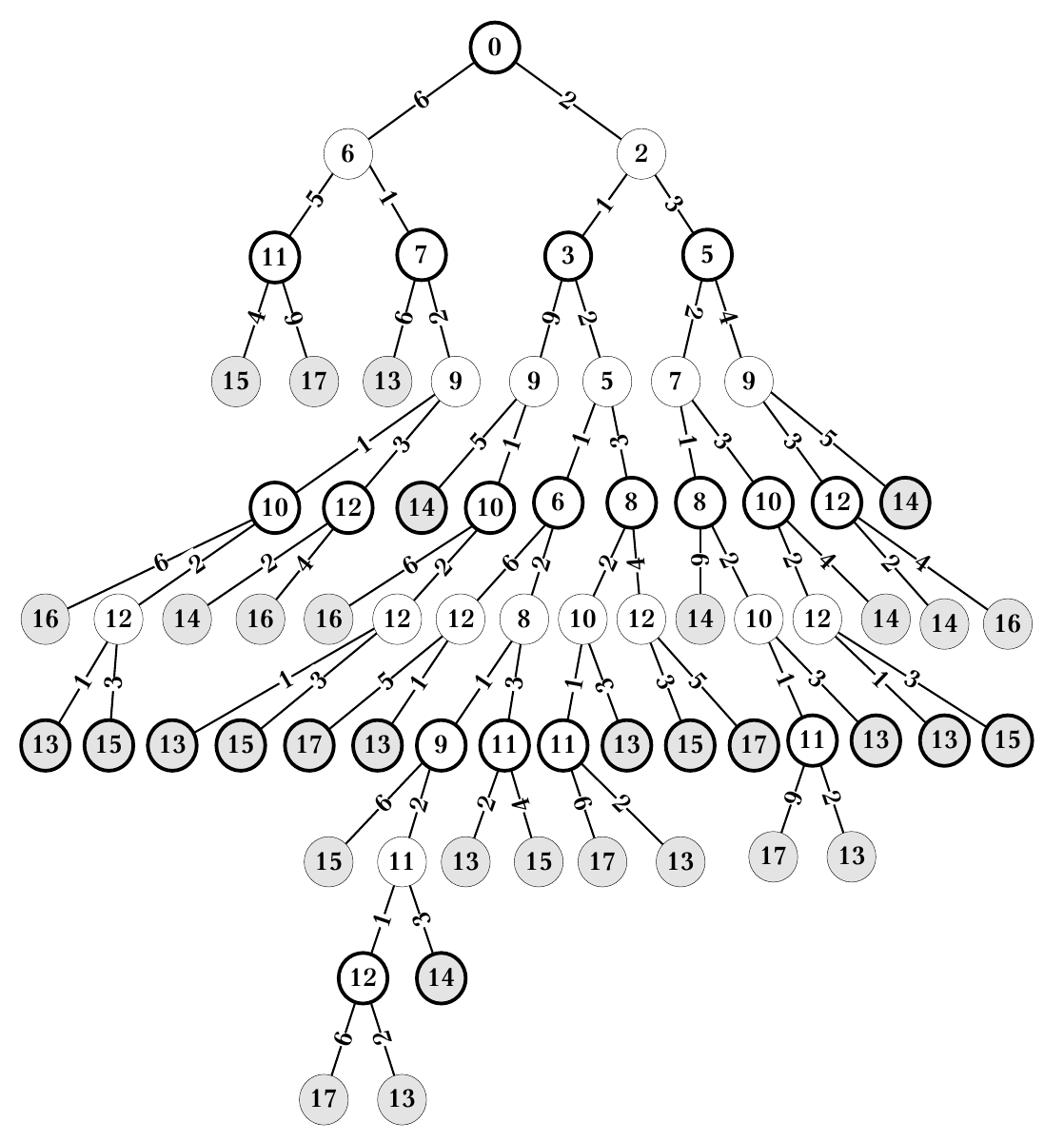
Fig. 83 Pilnas Lošimo disku medis, kai  ; medžio lapai
(t. y. baigiamosios žaidimo pozicijos pavaizduotos pilka spalva,
lyginių lygių pozicijos (iš kurių ėjimus atlieka pirmasis
žaidėjas), apvestos storesne linija; apskritimo viduje įrašyta s
reikšmė, o ant ėjimus žyminčių briaunų – žaidėjo ėjimai,
t. y. atsukamos disko pozicijos.¶
; medžio lapai
(t. y. baigiamosios žaidimo pozicijos pavaizduotos pilka spalva,
lyginių lygių pozicijos (iš kurių ėjimus atlieka pirmasis
žaidėjas), apvestos storesne linija; apskritimo viduje įrašyta s
reikšmė, o ant ėjimus žyminčių briaunų – žaidėjo ėjimai,
t. y. atsukamos disko pozicijos.¶
Pradėkime nuo 9-ojo lygio. Abi pozicijos yra baigiamosios ir
laiminčios tam žaidėjui, kuris atliko ėjimą, t. y. pirmajam.
Lipkime aukštyn į 8-ąjį lygį, kuriame galimos dvi pozicijos. Iš
pirmosios pozicijos ( ;
;  ) pirmasis
žaidėjas gali atlikti tik laiminčius ėjimus, taigi ši pozicija yra
laiminti pirmajam žaidėjui.
) pirmasis
žaidėjas gali atlikti tik laiminčius ėjimus, taigi ši pozicija yra
laiminti pirmajam žaidėjui.
Tuo tarpu antroji pozicija (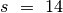 ;
; 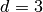 ) yra
baigiamoji žaidimo pozicija ir gaunama ėjimą atlikus antrajam
žaidėjui, taigi ji yra pralaiminti pirmojo žaidėjo pozicija.
) yra
baigiamoji žaidimo pozicija ir gaunama ėjimą atlikus antrajam
žaidėjui, taigi ji yra pralaiminti pirmojo žaidėjo pozicija.
7-ajame lygyje yra net 8 žaidimo pozicijos ir tik viena jų
(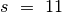 ;
; 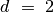 ) nėra baigiamoji. Visos baigiamosios
pozicijos yra laiminčios pirmajam žaidėjui, nes jos gaunamos pirmajam
žaidėjui atlikus ėjimą. O kaip gi su pozicija (
) nėra baigiamoji. Visos baigiamosios
pozicijos yra laiminčios pirmajam žaidėjui, nes jos gaunamos pirmajam
žaidėjui atlikus ėjimą. O kaip gi su pozicija (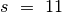 ;
;
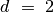 )?
)?
Iš šios pozicijos toliau ėjimą atliktų antrasis žaidėjas. Pasukęs diską, jis gali arba atsukti vienetą ir pakliūti į laiminčią pirmojo žaidėjo poziciją, arba atsukti trejetą ir laimėti pats. Žinoma, žaisdamas optimaliai, jis atsuks trejetą. Taigi ši pozicija yra pralaiminti pirmojo žaidėjo pozicija (Fig. 84 pav.)

Fig. 84 Žaidimo medžio fragmentas, pralaiminčios pirmojo žaidėjo pozicijos pažymėtos juodai¶
Šis pavyzdys ir paaiškina optimalios žaidimo strategijos esmę: jei tarp pozicijų, į kurias žaidėjas (nesvarbu kuris) gali pakliūti atlikęs ėjimą, yra nors viena laiminti to žaidėjo atžvilgiu, tai tas žaidėjas būtinai ją ir rinksis (Fig. 85 pav.).
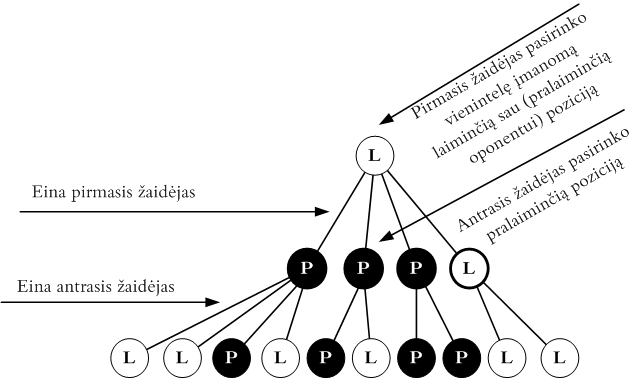
Fig. 85 Medžio pozicijos analizuojamos iš apačios į viršų; pirmojo žaidėjo laiminčios pozicijos žymimos L raide, pralaiminčios – P raide; jeigu eina pirmasis žaidėjas ir galima nors viena laiminti poziciją, jis ją ir renkasi; jeigu eina antrasis žaidėjas ir galima nors viena pralaiminti pirmojo žaidėjo pozicija, tai ji ir pasirenkama¶
Likusios pozicijos lipant medžiu aukštyn analogiškai suskirstomos į laiminčias ir pralaiminčias pirmojo žaidėjo pozicijas (žr. Fig. 86 pav.).
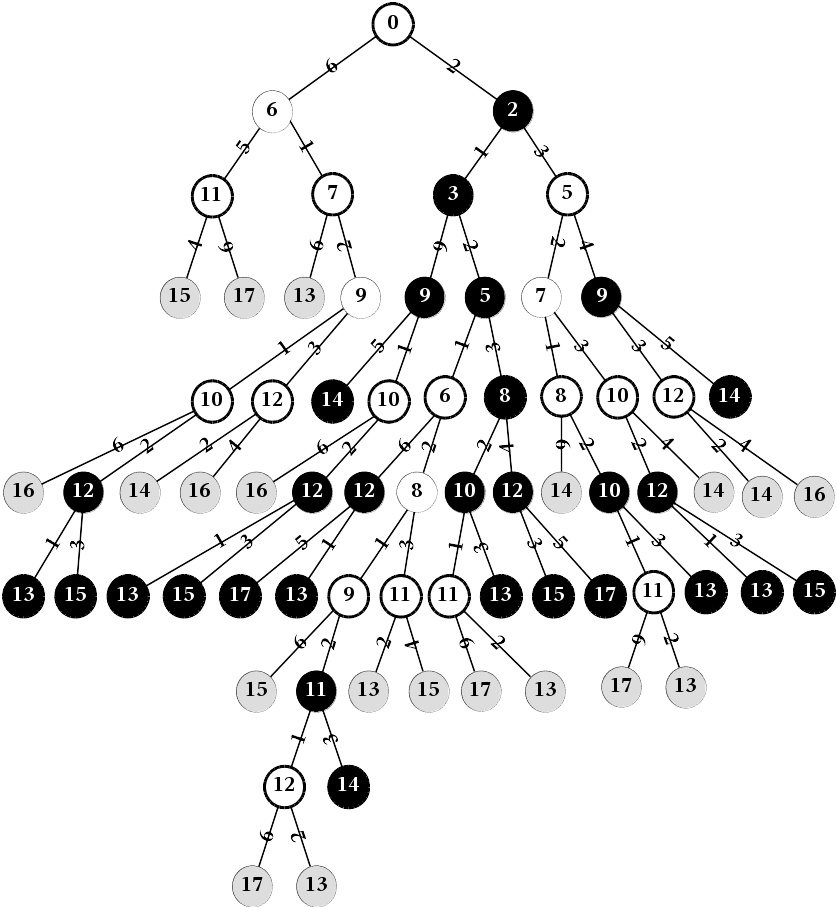
Fig. 86 Tas pats žaidimo medis kaip ir Fig. 83 pav., tik visos pozicijos suskirstytos į laiminčias ir pralaiminčias pirmajam žaidėjui; pralaiminčios pirmojo žaidėjo pozicijos pažymėtos juodai; matome, kad jei abu žaidėjai žaidžia optimaliai, pirmasis žaidėjas būtinai laimės¶
Užkopę iki pirmojo lygio matome, kad abiems žaidėjams žaidžiant optimaliai, laimės pirmasis.
Išanalizavę žaidimo medį (t.y. kiekvienai pozicijai priskyrę atributą, ar ji laiminti, ar pralaiminti) iš kiekvienos pozicijos galime pasirinkti palankiausią ėjimą. Deja, realybėje pilno žaidimo medžio dažniausiai suformuoti nepavyksta, tad apsiribojama tam tikru gyliu, iki kurio bus išskleidžiamas medis.
Pasiekus tą gylį, žaidimo pozicijos (pavadinkime jas ribinėmis), nors ir nėra baigiamosios, įvertinamos euristiškai. Pozicijos vertinamos skaičiais pasirinktame intervale [min_vertė, max_vertė]. Sutariama, kad pasirinkto žaidėjo (nevarbu kurio) laiminti pozicija bus vertinama maksimaliu intervalo skaičiumi max_vertė, o pralaiminti – minimaliu intervalo skaičiumi min_vertė. Šis žaidėjas dar vadinamas maksimizuojančiu žaidėju, o jo priešininkas – minimizuojančiu žaidėju.
Tad kuo geresnė yra pozicija maksimizuojančiam žaidėjui, tuo aukštesnį įvertinimą ji turėtų gauti. Ir atvirkščiai – kuo mažesnis pozicijos įvertinimas, tuo pozicija palankesnė minimizuojančiam žaidėjui. Ėjimo įverčiu vadinsime pozicijos, į kurią pakliūnama tuo ėjimu, įvertis.
Kol kas daugiau nesigilinsime į tai, kaip gaunami euristiniai pozicijų įverčiai 3, tiesiog laikysime, kad pasiekę ribinę poziciją galime gauti jos įvertį.
O kaip gi randamas bet kurios (nebūtinai ribinės ar baigiamosios)
žaidimo pozicijos įvertis? Tai atlieka MiniMax algoritmas:
rekursiškai iš viršaus į apačią formuojamas žaidimo medis ir
vertinamos pozicijos. Jei pozicija 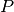 yra baigiamoji arba
ribinė, tai pozicija
yra baigiamoji arba
ribinė, tai pozicija 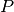 įvertinama tiksliai (pirmuoju atveju)
arba euristiškai (antruoju atveju). Jei pozicija
įvertinama tiksliai (pirmuoju atveju)
arba euristiškai (antruoju atveju). Jei pozicija 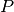 nėra
baigtinė, ir dar galima rekursiškai vertinti gilesnes pozicijas, tai
išbandomi visi galimi ėjimai ir išrenkamas bei grąžinamas geriausio
ėjimo įvertis.
nėra
baigtinė, ir dar galima rekursiškai vertinti gilesnes pozicijas, tai
išbandomi visi galimi ėjimai ir išrenkamas bei grąžinamas geriausio
ėjimo įvertis.
Jei iš pozicijos 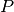 atliekant visus įmanomus ėjimus galima
pakliūti į pozicijas
atliekant visus įmanomus ėjimus galima
pakliūti į pozicijas 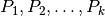 , o šių pozicijų
įverčiai jau yra žinomi:
, o šių pozicijų
įverčiai jau yra žinomi:
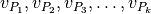 , tuomet pozicijos
, tuomet pozicijos
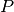 įvertis yra toks:
įvertis yra toks:
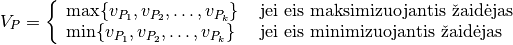
Kadangi šį algoritmą galima taikyti įvairiausiems žaidimas, tai neprisirišime prie konkretaus žaidimo ir algoritmą pateiksime pseudokodu 4:
MiniMax(gylis, pozicija, žaidėjas)
// „gylis“ nurodo iki kokio lygio skleisime žaidimo medį
// „pozicija“ parodo nuo kokios pozicijos analizuosime žaidimą
jei žaidėjas yra maksimizuojantis
tai grąžink Max(gylis, pozicija)
kitu atveju grąžink Min(gylis, pozicija)
Max(gylis, pozicija)
jei žaidimas baigtas arba (gylis = 0)
tai grąžink įvertinimas(pozicija, mini\_zaid)
// įvertinama pozicija, kai paskutinį ėjimą atliko
// minimizuojantis žaidėjas
kitu atveju
geriausias := MIN_VERTĖ
kiekvienam galimam ėjimui e
atlik ėjimą(e, pozicija)
įvertis := Min(gylis - 1, pozicija)
jei įvertis > geriausias tai
geriausias = įvertis
atšauk ėjimą(e, pozicija)
grąžink geriausias
Min(gylis, pozicija)
// ** pažymėtos tos procedūros Min eilutės, kurios skiriasi
// nuo procedūros Max.
jei žaidimas baigtas arba (gylis = 0)
tai grąžink įvertinimas(pozicija, max_zaid) //**
// įvertinama pozicija, kai paskutinį ėjimą atliko
// maksimizuojantis žaidėjas
kitu atveju
geriausias := MAX_VERTĖ //**
kiekvienam galimam ėjimui e
atlik ėjimą(e, pozicija)
įvertis := Max(gylis - 1, pozicija) //**
jei įvertis < geriausias tai //**
geriausias = įvertis
atšauk ėjimą(e, pozicija)
grąžink geriausias
Realiose situacijose žaidimo pozicija dažnai nusakoma sudėtinga duomenų struktūra ir ji neperduodama per parametrus, bet pasiekiama kaip globalusis kintamasis.
Pritaikysime šį algoritmą Lošimui su disku. Kol kas detaliau
nesiaiškinome, kaip euristiškai vertinti pozicijas, tačiau, kaip
matėme, kai 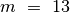 , žaidimo medį galima išskleisti pilnai.
Tad realizuodami algoritmą taip pat laikysime, kad žaidimo medį
galima pilnai išskleisti. Žaidžiant šį žaidimą galimi tik du
skirtingi pozicijų įverčiai – laiminti ir pralaiminti (lygiųjų
būti negali), tad pozicijas vertinsime ne skaičiais, o loginėmis
reikšmėmis: „minimali“ pozicijos vertė bus
, žaidimo medį galima išskleisti pilnai.
Tad realizuodami algoritmą taip pat laikysime, kad žaidimo medį
galima pilnai išskleisti. Žaidžiant šį žaidimą galimi tik du
skirtingi pozicijų įverčiai – laiminti ir pralaiminti (lygiųjų
būti negali), tad pozicijas vertinsime ne skaičiais, o loginėmis
reikšmėmis: „minimali“ pozicijos vertė bus false,
„maksimali“ – true.
const M = 13; { šį skaičių pasiekęs ar viršijęs, žaidėjas laimi }
type Tpozicija = record
s, d : integer;
{ s ir d nusako konkrečią žaidimo poziciją }
end;
procedure atlik_ėjimą(sukti_pirmyn : boolean;
var p : Tpozicija);
begin
if sukti_pirmyn then
p.d := (p.d + 4) mod 6 + 1
else
p.d := p.d mod 6 + 1;
p.s := p.s + p.d;
end;
procedure atšauk_ėjimą(sukti_pirmyn : boolean;
var p : Tpozicija);
begin
p.s := p.s - p.d;
if sukti_pirmyn then
p.d := p.d mod 6 + 1
else
p.d := (p.d + 4) mod 6 + 1;
end;
function Min(pozicija : TPozicija) : boolean; forward;
function Max(pozicija : TPozicija) : boolean;
{ randa pozicijos įvertį (ar tai laiminti pirmojo žaidėjo pozicija),
jei ėjimą iš jos atlieka pirmasis (maksimizuojantis) žaidėjas }
var sukti_pirmyn, įvertis : boolean;
begin
if pozicija.s >= M then { jei žaidimas baigtas }
Max := false
{ nes paskutinį ėjimą atliko antrasis žaidėjas }
else begin
Max := false;
for sukti_pirmyn := false to true do begin
atlik_ėjimą(sukti_pirmyn, pozicija);
įvertis := Min(pozicija);
if (Max = false) and (įvertis = true)
then { jei Max < įvertis }
Max := įvertis;
atšauk_ėjimą(sukti_pirmyn, pozicija);
end;
end;
end;
function Min(pozicija : TPozicija) : boolean;
{ randa pozicijos įvertį (ar tai laiminti pirmojo žaidėjo pozicija),
jei ėjimą iš jos atlieka antrasis (minimizuojantis) žaidėjas }
var sukti_pirmyn, įvertis : boolean;
begin
if pozicija.s >= M then { jei žaidimas baigtas }
Min := true
{ nes paskutinį ėjimą atliko pirmasis žaidėjas }
else begin
Min := true;
for sukti_pirmyn := false to true do begin
atlik_ėjimą(sukti_pirmyn, pozicija);
įvertis := Max(pozicija);
if (Min = true) and (įvertis = false)
then { jei Min > įvertis }
Min := įvertis;
atšauk_ėjimą(sukti_pirmyn, pozicija);
end;
end;
end;
function MiniMax(žaidėjas : integer;
pozicija : Tpozicija) : boolean;
{ randa pozicijos įvertį („true“, jei tai laiminti pirmojo žaidėjo pozicija
ir „false“ priešingu atveju }
begin
if žaidėjas = 1 then
{ jei ėjimą atliks pirmasis (maksimizuojantis) žaidėjas }
MiniMax := Max(pozicija)
else
MiniMax := Min(pozicija);
end;
const int M = 13; // šį skaičių pasiekęs ar viršijęs, žaidėjas laimi
struct tPozicija {
int s, d; // s ir d nusako konkrečią žaidimo poziciją
};
void atlikEjima (bool suktiPirmyn, tPozicija &p) {
if (suktiPirmyn)
p.d = (p.d + 4) % 6 + 1;
else
p.d = p.d % 6 + 1;
p.s += p.d;
}
void atsaukEjima (bool suktiPirmyn, tPozicija &p) {
p.s -= p.d;
if (suktiPirmyn)
p.d = p.d % 6 + 1;
else
p.d = (p.d + 4) % 6 + 1;
}
bool minIvertis (tPozicija pozicija);
bool maxIvertis (tPozicija pozicija) {
/*
randa pozicijos įvertį (ar tai laiminti pirmojo žaidėjo pozicija),
jei ėjimą iš jos atlieka pirmasis (maksimizuojantis) žaidėjas
*/
if (pozicija.s >= M) // jei žaidimas baigtas
return false; // nes paskutinį ėjimą atliko antrasis žaidėjas
else {
bool grazinamasIvertis = false;
bool kryptys[] = {false, true};
for(bool suktiPirmyn : kryptys) { {
atlikEjima(suktiPirmyn, pozicija);
bool ivertis = minIvertis(pozicija);
if (!grazinamasIvertis && ivertis) // jei grazinamasIvertis < ivertis
grazinamasIvertis = ivertis;
atsaukEjima(suktiPirmyn, pozicija);
}
}
}
bool minIvertis (tPozicija pozicija) {
/*
randa pozicijos įvertį (ar tai laiminti pirmojo žaidėjo pozicija),
jei ėjimą iš jos atlieka antrasis (minimizuojantis) žaidėjas
*/
if (pozicija.s >= M) // jei žaidimas baigtas
return true; // nes paskutinį ėjimą atliko pirmasis žaidėjas
else {
bool grazinamasIvertis = true;
bool kryptys[] = {false, true};
for(bool suktiPirmyn : kryptys) { {
atlikEjima(suktiPirmyn, pozicija);
bool ivertis = maxIvertis(pozicija);
if (grazinamasIvertis && !ivertis) // jei grazinamasIvertis > ivertis
grazinamasIvertis = ivertis;
atsaukEjima(suktiPirmyn, pozicija);
}
}
}
bool miniMax (int zaidejas, tPozicija pozicija) {
/*
randa pozicijos įvertį ("true", jei tai laiminti
pirmojo žaidėjo pozicija ir "false" priešingu atveju
*/
if (zaidejas == 1) // jei ėjimą atliks pirmasis (maksimizuojantis) žaidėjas
return maxIvertis(pozicija);
else
return minIvertis(pozicija);
}
Euristinis pozicijų vertinimas bei iteratyvus paieškos gilinimas¶
Kaip jau minėta, dažnai pilno žaidimo medžio suformuoti nepavyksta ir pasiekus ribinį gylį žaidimo pozicijas tenka vertinti euristiškai. Jeigu medį galima išskleisti pilnai, užtenka trijų tipų pozicijų: laiminčių, pralaiminčių ir lygiųjų. Tuo tarpu euristinis pozicijos vertinimas yra kur kas sudėtingesnis. Tai atliekant reikia panaudoti kuo daugiau žinių apie konkretų žaidimą.
Euristinis pozicijos įvertis gaunamas žaidimo poziciją įvertinant skaičiumi. Maksimizuojantis ir minimizuojantis žaidėjai turi vertinti žaidimą analogiškai. Pavyzdžiui, vienas žaidėjas mano, kad yra geroje pozicijoje, tai jo oponentas turi manyti, kad jis (t. y. oponentas) yra prastoje pozicijoje.
Euristiškai vertinant pozicijas dažniausiai sudaroma tokio tipo įvertinimo funkcija:
Įvertis(pozicija) =
kur 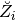 yra skaičiais išreikštos tam tikros žinios
apie žaidimą, įvertinančios poziciją kažkokiu konkrečiu aspektu,
o
yra skaičiais išreikštos tam tikros žinios
apie žaidimą, įvertinančios poziciją kažkokiu konkrečiu aspektu,
o 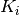 – koeficientai, suteikiantys žinioms skirtingą svorį.
– koeficientai, suteikiantys žinioms skirtingą svorį.
Euristinės įvertinimo funkcijos dažniausiai turi dėmenis, kuriuose kaupiamos tokio tipo žinios apie žaidimą:
materialūs įverčiai; pavyzdžiui, šachmatų ar šaškių figūrų skaičius lentoje arba savo ir priešininko figūrų kiekių skirtumas (šachmatuose kiekvienos rūšies figūrai dažnai suteikiamas svoris);
erdvė; kai kuriuose žaidimuose yra labai svarbu, kiek erdvės kontroliuoja vienas ar kitas žaidėjas, taigi žaidėjo kontroliuojamą erdvę galima išreikšti skaičiumi ir įtraukti į įvertinimo funkciją;
mobilumas; kiek ėjimų galima atlikti iš esamos pozicijos; t. y. tikėtina, kad jei turite daugiau galimybių paeiti, didesnė tikimybė, kad bent vienas šių ėjimų nuves į gerą poziciją; šis įvertis nepasitvirtino kuriant šachmatų žaidimo algoritmus, tačiau pasirodė labai naudingas žaidžiant, pavyzdžiui, Otelo;
tempas; kai kuriuose žaidimuose yra svarbu tai, kuris žaidėjas turi iniciatyvą, o kuris tik atsako į priešininko ėjimus (pavyzdžiui, galbūt jūsų figūra yra puolama ir jai teks trauktis);
grėsmės; kiek jūsų figūrų yra puolama, gal gali atsitikti dar kažkas negero, pavyzdžiui, pėstininkas taps valdove arba oponentas užims dalį jūsų teritorijos;
forma; kai kuriuose žaidimuose yra gan svarbu, kaip išsidėstę figūros; pavyzdžiui, šachmatuose gretimuose stulpeliuose vienas paskui kitą stovintys pėstininkai laikomi stipresne kombinacija, nei tame pačiame stulpelyje esantys pėstininkai;
išskirtinės situacijos; beveik kiekviename žaidime pasitaiko išskirtinių situacijų, kuriose žmogus žino, kaip geriausia sužaisti; kartais verta paaukoti figūrą ir taip laimėti dar daugiau; tam tikros išskirtinės situacijos taip gali būti įtrauktos į euristinį vertinimą.
Deja, kuo daugiau žinių apie žaidimą įtraukiame į programą, tuo lėčiau programa veikia. Greitą ir prastai žaidžiančią programą galima pagerinti į algoritmą įtraukiant daugiau žinių apie žaidimą. Tačiau šios papildomos žinios gali padaryti programą lėtesne (per leistiną laiką spėjančią išanalizuoti mažiau žaidimo lygių) ir tada ji gali žaisti netgi prasčiau nei prieš tobulinimą. Taigi reikia išlaikyti tinkamą balansą tarp efektyvumo ir žinių.
O kaip gi apskaičiuoti ribinį gylį, kurį pasiekus reiktų daugiau nebesiplėsti ir pradėti vertinti pozicijas euristiškai? Programuojant žaidimų algoritmus taikoma gan paprasta strategija: MiniMax algoritmas įvykdomas analizuojant pozicijas iki pirmojo gylio, po to (jeigu dar užtenka laiko) – MiniMax algoritmas vykdomas iš naujo, tik pozicijos analizuojamos iki antrojo gylio, tuomet – jei dar užtenka laiko – iki trečiojo gylio ir taip toliau, kol išnaudojami laiko ar atminties limitai. Tai ir yra iteratyvus paieškos gilinimas. Toliau pateiktas algoritmas atlieka iteratyvų paieškos gilinimą maksimizuojančiam žaidėjui.
Rask_ėjimą(pozicija, žaidėjas)
gylis = 0
kol neužtrukta daug laiko
gylis = gylis + 1
pozicija := PRADINĖ
geriausias_įvertis := MIN_VERTĖ
kiekvienam galimam žaidėjo ėjimui e
atlik ėjimą(e, pozicija)
įvertis :=
Minimax(gylis, pozicija, žaidėjas);
jei įvertis > geriausias_įvertis
tai geriausias_įvertis := įvertis
geriausias_ėjimas := e
atšauk ėjimą(e, pozicija)
grąžink geriausias_ėjimas
Tai gali pasirodyti labai neefektyvu, mat vykdant kitą iteraciją
ankstesni skaičiavimai nepanaudojami. Iš tiesų tai nėra taip
neefektyvu kaip atrodo iš pirmo žvilgsnio, kadangi nagrinėjamų
pozicijų skaičius didinant gylį auga eksponentiškai. Taigi laikas,
reikalingas algoritmo vykdymui iki gylio  , yra dažniausiai
daug didesnis už laiką, reikalingą paieškai iki gylio
, yra dažniausiai
daug didesnis už laiką, reikalingą paieškai iki gylio
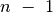 . Tarkime, kad kiekviename lygyje iš kiekvienos
pozicijos galima atlikti
. Tarkime, kad kiekviename lygyje iš kiekvienos
pozicijos galima atlikti 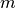 ėjimų.
ėjimų.
Tuomet paieškai iki gylio  užtrunkama
užtrunkama
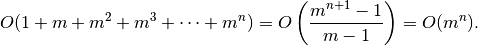
Jei paieška bus gilinama iteratyviai, tuomet bus užtrunkama
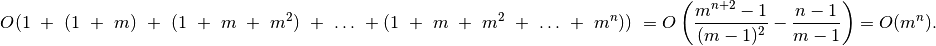
Alfa-Beta atkirtimas¶
Minimax paieška nėra efektyvi, nes išnagrinėjami visi galimi ėjimai, o jų kiekis, ieškant gilyn, auga eksponentiškai. Tačiau ar būtina išanalizuoti visus galimus ėjimus ir rasti kiekvieno ėjimo (tiksliau pozicijos, į kurią pakliūvama atlikus tą ėjimą) įvertį? Panagrinėkime Fig. 87 paveiksle pateiktą situaciją.
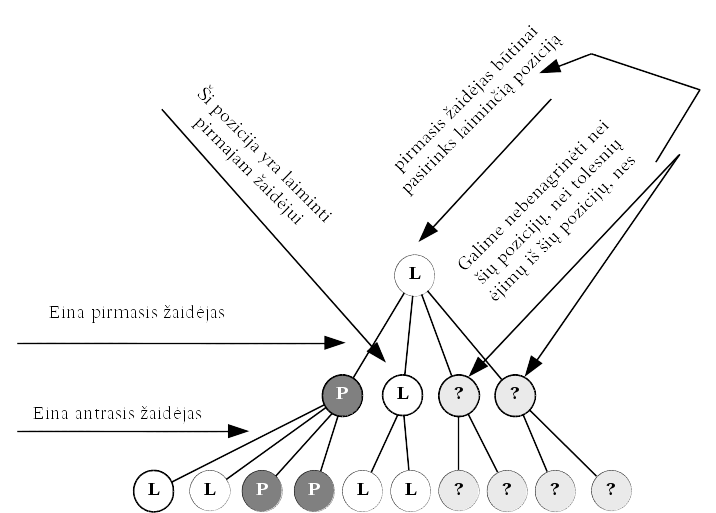
Fig. 87 Pavyzdys, kai nebūtina analizuoti visų žaidimo pozicijų; laiminti pirmojo žaidėjo pozicija pažymėta L raide, pralaiminti – P raide¶
Matome, kad dar neišanalizavus viso žaidimo medžio galima nustatyti, kurį ėjimą pasirinks vienas ar kitas žaidėjas ir nebeanalizuoti dalies ėjimų. Kitaip sakant galima atkirsti kai kurias žaidimo medžio šakas. Atkirtimas gali būti taikomas ir tiems žaidimų medžiams, kuriuos pavyksta pilnai išskleisti, ir tiems, kurių pozicijos vertinamos euristiškai.
Atkirtimą realizuoja Alfa-Beta algoritmas, kuris grindžiamas tokia
idėja: jei jau rastas neblogas ėjimas  , ir matosi, kad kitas
šiuo metu analizuojamas ėjimas nuves į blogesnę poziciją, nei
būtų galima pasiekti pasirinkus
, ir matosi, kad kitas
šiuo metu analizuojamas ėjimas nuves į blogesnę poziciją, nei
būtų galima pasiekti pasirinkus  , tuomet pozicijos, (ir
tolesnių ėjimų iš jos) į kurią pakliūnama tuo kitu ėjimu, galima
nebenagrinėti.
, tuomet pozicijos, (ir
tolesnių ėjimų iš jos) į kurią pakliūnama tuo kitu ėjimu, galima
nebenagrinėti.
Pastebėsime, kad Alfa-Beta algoritmas savo esme yra Minimax algoritmas, papildytas dviem atkirtimo kriterijais. Minimax algoritmas analizuoja visus galimus ėjimus iš konkrečios pozicijos ir parenka ėjimą su palankiausiu įverčiu, o Alfa-Beta atkirtimo algoritmas neanalizuoja ėjimų, jei mato, kad jų įverčiai bus prastesni už palankiausią iki šiol rastą įvertį.
Sutarsime sakyti, kad žaidėjas užsitikrino vertę  , jeigu
jis gali parinkti tokią ėjimų seką, kad nesvarbu kaip žaistų jo
priešininkas, žaidėjas pasieks poziciją, kurios vertė lygi
, jeigu
jis gali parinkti tokią ėjimų seką, kad nesvarbu kaip žaistų jo
priešininkas, žaidėjas pasieks poziciją, kurios vertė lygi
 arba dar palankesnė, t. y. didesnė už
arba dar palankesnė, t. y. didesnė už  , jei tai
maksimizuojantis žaidėjas arba mažesnė už
, jei tai
maksimizuojantis žaidėjas arba mažesnė už  , jei tai
minimizuojantis žaidėjas (Fig. 88 pav.).
, jei tai
minimizuojantis žaidėjas (Fig. 88 pav.).
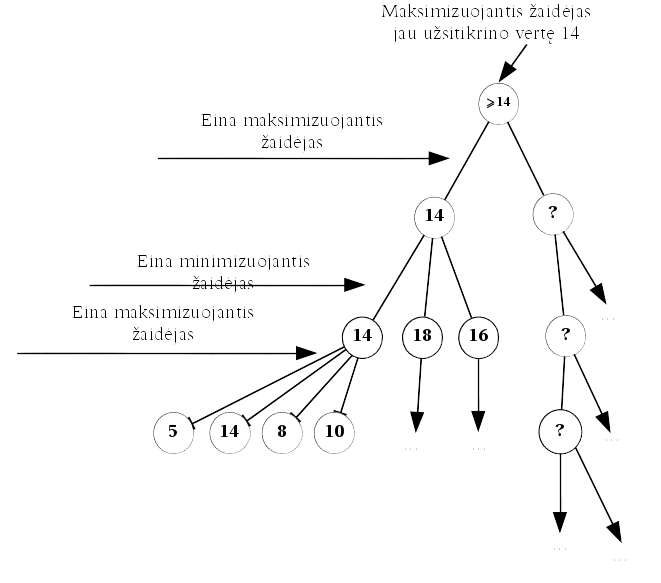
Fig. 88 Maksimizuojantis žaidėjas gali parinkti tokią ėjimų
seką, kad nesvarbu kaip žaistų jo priešininkas, maksimizuojantis
žaidėjas pasieks poziciją, kurios vertė lygi 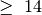 ,
t. y. jis užsitikrino vertę 14¶
,
t. y. jis užsitikrino vertę 14¶
Alfa-Beta algoritmas operuoja parametrais alfa ir beta. Parametre
alfa saugoma minimali vertė, kurią jau užsitikrino maksimizuojantis
žaidėjas konkrečiai pozicijai  , o parametre beta –
maksimali vertė, kurią tai pačiai pozicijai užsitikrino
minimizuojantis žaidėjas. Pradiniu momentu alfa reikšmė lygi
, o parametre beta –
maksimali vertė, kurią tai pačiai pozicijai užsitikrino
minimizuojantis žaidėjas. Pradiniu momentu alfa reikšmė lygi
min_vertė, o beta – max_vertė.
Kadangi maksimizuojantis žaidėjas renkasi ėjimus su kuo didesniu įverčiu, o minimizuojantis – su kuo mažesniu, tai maksimizuojantis žaidėjas siekia, kad alfa reikšmė būtų kuo didesnė, o jo oponentas – kad beta reikšmė būtų kuo mažesnė.
Sakykime, jau išnagrinėta dalis žaidimo medžio ir maksimizuojantis žaidėjas užsitikrino alfa vertę. Tačiau tikintis dar geresnio rezultato, nagrinėjama ir likusi medžio dalis.
Tarkime, kad bet kur toliau medyje minimizuojančiam žaidėjui atlikus
ėjimą iš pozicijos  pakliūta į poziciją
pakliūta į poziciją 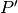 , o
pastarosios vertė
, o
pastarosios vertė 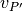 yra mažesnė už alfa. Tuomet
akivaizdu, kad minimizuojantis žaidėjas iš pozicijos
yra mažesnė už alfa. Tuomet
akivaizdu, kad minimizuojantis žaidėjas iš pozicijos 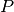 rinkdamasis ėjimą su kuo mažesne verte pasieks, kad
rinkdamasis ėjimą su kuo mažesne verte pasieks, kad
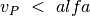 . Taigi pozicija
. Taigi pozicija 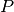 maksimizuojančiam
žaidėjui nebeįdomi ir likusių ėjimų iš
maksimizuojančiam
žaidėjui nebeįdomi ir likusių ėjimų iš 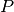 galima
nebenagrinėti (Fig. 89 pav.).
galima
nebenagrinėti (Fig. 89 pav.).
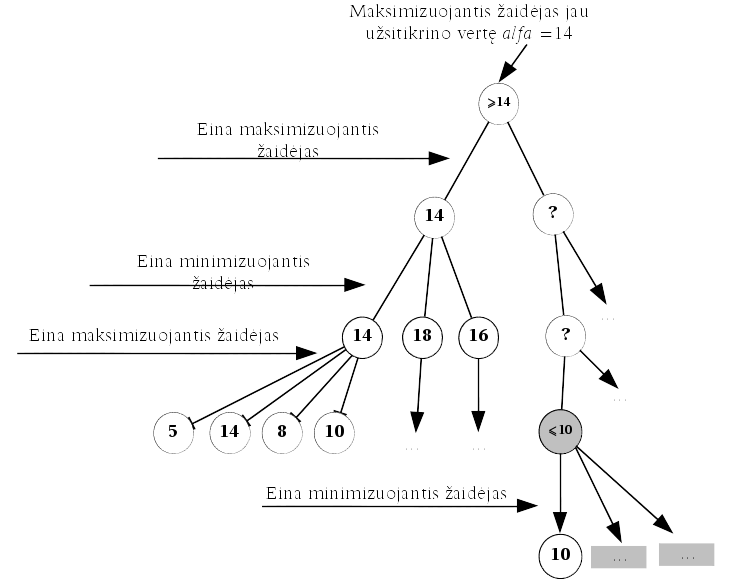
Fig. 89 Maksimizuojantis žaidėjas gali parinkti tokią ėjimų
seką, kad nesvarbu kaip žaistų jo priešininkas, maksimizuojantis
žaidėjas pasieks poziciją, kurios vertė lygi 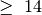 ,
t. y. jis užsitikrino vertę 14¶
,
t. y. jis užsitikrino vertę 14¶
Tarkime, kad bet kur toliau medyje maksimizuojančiam žaidėjui atlikus
ėjimą iš pozicijos 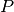 pakliūta į poziciją
pakliūta į poziciją 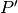 , o
pastarosios vertė
, o
pastarosios vertė 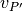 yra didesnė už beta, tuomet
akivaizdu, kad maksimizuojantis žaidėjas iš pozicijos
yra didesnė už beta, tuomet
akivaizdu, kad maksimizuojantis žaidėjas iš pozicijos 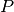 rinkdamasis ėjimą su kuo didesne verte pasieks, kad
rinkdamasis ėjimą su kuo didesne verte pasieks, kad
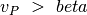 . Taigi pozicija
. Taigi pozicija 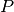 minimizuojančiam
žaidėjui nebeįdomi ir likusių ėjimų iš
minimizuojančiam
žaidėjui nebeįdomi ir likusių ėjimų iš 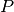 galima
nebenagrinėti (Fig. 90 pav.).
galima
nebenagrinėti (Fig. 90 pav.).

Fig. 90 Minimizuojantis žaidėjas gali parinkti tokią ėjimų
seką, kad nesvarbu kaip žaistų jo priešininkas, minimizuojantis
žaidėjas pasieks poziciją, kurios vertė lygi 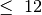 ,
t. y. jis užsitikrino vertę 12¶
,
t. y. jis užsitikrino vertę 12¶
Alfa-Beta(gylis, pozicija, žaidėjas)
{ „gylis“ nurodo iki kokio lygio skleisime žaidimo medį
„pozicija“ parodo nuo kokios pozicijos analizuosime žaidimą }
jei žaidėjas yra maksimizuojantis
tai grąžink
Alfa-Beta-Max(gylis, pozicija, MAX\_VERTĖ)
{ perduodama MAX_VERTĖ, taigi šioje pozicijoje nebus
vykdomas atkirtimas }
kitu atveju grąžink
Alfa-Beta-Min(gylis, pozicija, MIN\_VERTĖ)
{ perduodama MIN_VERTĖ, taigi šioje pozicijoje nebus
vykdomas atkirtimas }
Alfa-Beta-Max(gylis, pozicija, beta)
jei žaidimas baigtas arba (gylis = 0)
tai grąžink įvertinimas(pozicija, mini\_zaid)
kitu atveju
alfa = MIN_VERTĖ // alfa – lokalus kintamasis
kiekvienam galimam ėjimui e
atlik ėjimą(e, pozicija)
įvertis := Alfa-Beta-Min(
gylis – 1, pozicija, alfa)
atšauk ėjimą(e, pozicija)
jei beta <= įvertis
tai grąžink alfa // atliekamas atkirtimas
jei įvertis > alfa
tai alfa = įvertis
grąžink alfa
Alfa-Beta-Min(gylis, pozicija, alfa)
{ alfa ir beta yra lokalūs kintamieji }
jei žaidimas baigtas arba (gylis = 0)
tai grąžink įvertinimas(pozicija, max\_zaid)
kitu atveju
beta = MAX_VERTĖ // beta – lokalus kintamasis
kiekvienam galimam ėjimui e
atlik ėjimą(e, pozicija)
įvertis := Alfa-Beta-Max(
gylis – 1, pozicija, beta)
atšauk ėjimą(e, pozicija)
jei įvertis <= alfa
tai grąžink beta // atliekamas atkirtimas
jei įvertis < beta
tai beta = įvertis
grąžink beta
Alfa-Beta atkirtimo efektyvumas labai priklauso nuo to, kokia tvarka nagrinėjami ėjimai. Jeigu visą laiką pirmiau aptinkami blogiausi ėjimai, tokiu atveju algoritmas veiks lygiai taip pat, kaip ir Minimax algoritmas ir iš esmės atkirtimas niekada nebus atliktas. Todėl tvarka, kuria peržiūrimi ėjimai labai svarbi atliekant Alfa-Beta atkirtimą.
Išnašos
- 1
Žaidimų programų olimpiadas kasmet organizuoja ICGA (International Computer Games Association); Olandijos informatikos olimpiados kasmet organizuoja žaidimų programų turnyrą CodeCup.
- 2
Panašus uždavinys buvo pateiktas Lietuvos informatikos olimpiadoje III etape 1998 metais.
- 3
Apie euristinį pozicijų vertinimą detaliau kalbama skyrelyje Euristinis pozicijų vertinimas bei iteratyvus paieškos gilinimas.
- 4
Pseudokodas yra algoritmo aprašymas, kai naudojami programavimo kalbų struktūriniai elementai, tačiau praleidžiami kalbai būdingi sintaksės elementai.