Pirmasis algoritmas – Euklido algoritmas didžiausiam bendrajam dalikliui rasti¶
Kartą mokinys, išmokęs savo pirmąją geometrijos teoremą,paklausė Euklido: „Kokia man nauda, kad šitai išmoksiu?“.Euklidas pakvietė savo vergą ir tarė: „Duok šiam žmoguidrachmą, nes jis turi turėti naudos iš to, ką išmoksta.“J. Stobijus (Joannes Stobaeus), V a. pr. Kr.

Fig. 4 Euklido portretas¶
Šiame skyrelyje susipažinsime su seniausiu netrivialiu algoritmu, išlikusiu iki šių dienų. Tai algoritmas didžiausiam bendrajam dalikliui rasti. Nėra žinoma, kas šį algoritmą sugalvojo (ir ar tai buvo vienas žmogus). Dar prieš Euklidui (graikų k. Εὐκλείδης, Eukleides) aprašant šį algoritmą, jį savo veikale cituoja Aristotelis. Euklidas algoritmą kruopščiai aprašė garsiajame veikale „Pradmenys“ (apie 300 m. pr. Kr.), todėl algoritmui ir prigijo Euklido vardas.
Didžiausias bendrasis daliklis ir mažiausias bendrasis kartotinis¶
Prisiminkime didžiausio bendrojo daliklio (DBD) ir mažiausio bendrojo kartotinio (MBK) sąvokas.
Sakome, kad skaičius 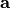 dalija skaičių
dalija skaičių
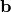 , jei egzistuoja toks sveikasis skaičius
, jei egzistuoja toks sveikasis skaičius  ,
kad
,
kad 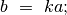 žymime
žymime 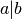 .
.
Pavyzdžiui, 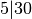 , nes
, nes 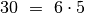 . Skaičius 1
dalija visus skaičius (
. Skaičius 1
dalija visus skaičius (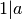 , visiems sveikiesiems
, visiems sveikiesiems  ), o
skaičių 0 dalija visi skaičiai, išskyrus patį 0 (
), o
skaičių 0 dalija visi skaičiai, išskyrus patį 0 (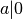 ,
visiems sveikiesiems
,
visiems sveikiesiems  ,
, 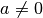 ).
).
Dviejų neneigiamų skaičių  ir
ir 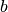 didžiausiu
bendruoju dalikliu (DBD) vadinamas didžiausias skaičius, dalijantis
didžiausiu
bendruoju dalikliu (DBD) vadinamas didžiausias skaičius, dalijantis
 ir
ir 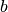 . Pavyzdžiui,
. Pavyzdžiui, 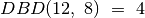 ,
,
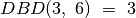 ,
, 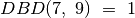 .
.
Neneigiamų skaičių  ir
ir 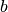 mažiausiu bendruoju
kartotiniu (MBK) vadinamas mažiausias teigiamas skaičius, kurį
dalija
mažiausiu bendruoju
kartotiniu (MBK) vadinamas mažiausias teigiamas skaičius, kurį
dalija  ir
ir 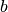 . Pavyzdžiui,
. Pavyzdžiui, 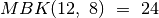 ,
,
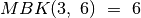 ,
, 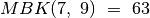 .
.
Natūralus būdas rasti 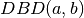 – išskaidyti skaičius
– išskaidyti skaičius
 ir
ir 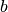 pirminiais daugikliais ir išrinkti visus
bendruosius šių skaičių pirminius daugiklius. Pavyzdžiui,
pirminiais daugikliais ir išrinkti visus
bendruosius šių skaičių pirminius daugiklius. Pavyzdžiui,
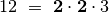 ,
,
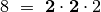 , bendrieji
daugikliai yra
, bendrieji
daugikliai yra 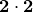 , taigi
, taigi
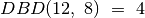 . Šiuo būdu tarsi konstruojame
. Šiuo būdu tarsi konstruojame 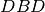 ,
stengdamiesi jį padaryti kuo didesnį (rinkdami kuo daugiau skaičiaus
,
stengdamiesi jį padaryti kuo didesnį (rinkdami kuo daugiau skaičiaus
 pirminių daugiklių), tačiau žiūrėdami, kad
pirminių daugiklių), tačiau žiūrėdami, kad 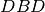 dalytų ir skaičių
dalytų ir skaičių 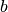 .
.
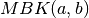 taip pat galime rasti išskaidę skaičius
taip pat galime rasti išskaidę skaičius  ir
ir 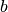 į pirminius daugiklius. Kadangi
į pirminius daugiklius. Kadangi 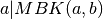 , tai
, tai
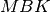 turi priklausyti visi
turi priklausyti visi  pirminiai daugikliai.
Tačiau ir
pirminiai daugikliai.
Tačiau ir 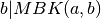 , todėl pridedame skaičiaus
, todėl pridedame skaičiaus 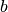 pirminius daugiklius, kurių trūksta (būtent, daugiklius, kurie nėra
bendrieji skaičiams
pirminius daugiklius, kurių trūksta (būtent, daugiklius, kurie nėra
bendrieji skaičiams  ir
ir 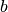 ). Pavyzdžiui,
). Pavyzdžiui,
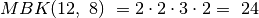 .
.
Šie 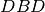 ir
ir 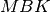 konstravimo būdai paaiškina ir šiuos
skaičius siejančią lygybę:
konstravimo būdai paaiškina ir šiuos
skaičius siejančią lygybę: 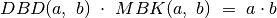 .
.
Euklido algoritmas¶
Tarkime, reikia rasti skaičių  ir
ir 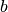 didžiausiąjį
bendrą daliklį. Atliekame tokius veiksmus:
didžiausiąjį
bendrą daliklį. Atliekame tokius veiksmus:
jei
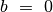 , tai
, tai 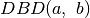 lygus
lygus  ,
priešingu atveju
,
priešingu atveju 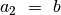 ,
, 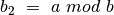 (lygus liekanai, gautai padalijus
(lygus liekanai, gautai padalijus  iš
iš 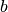 )
)jei
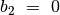 , tai
, tai 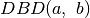 lygus
lygus 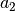 ,
priešingu atveju
,
priešingu atveju 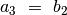 ,
,
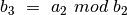
…
jei
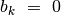 , tai
, tai 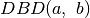 lygus
lygus 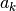 ,
priešingu atveju
,
priešingu atveju 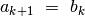 ,
,
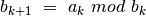 .
.
Kadangi dalydami iš skaičiaus  galime gauti liekaną nuo 0
iki
galime gauti liekaną nuo 0
iki 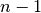 , tai
, tai
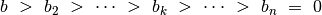 ,
ir algoritmas atliks baigtinį skaičių veiksmų (anksčiau ar vėliau
,
ir algoritmas atliks baigtinį skaičių veiksmų (anksčiau ar vėliau
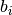 taps lygus 0, tad algoritmas baigs darbą).
taps lygus 0, tad algoritmas baigs darbą).
Raskime skaičių 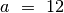 ir
ir 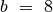
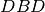 naudodamiesi Euklido algoritmu:
naudodamiesi Euklido algoritmu:
 , taigi skaičiuojame
, taigi skaičiuojame 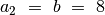 ,
,
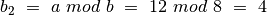 .
.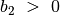 , taigi skaičiuojame
, taigi skaičiuojame
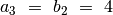 ,
,
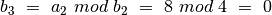 .
.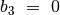 , taigi
, taigi 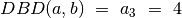 .
.
Gavome 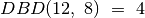 . Užrašysime Euklido algoritmą Paskalio ir C++ kalbomis.
. Užrašysime Euklido algoritmą Paskalio ir C++ kalbomis.
function DBD(a, b : longint) : longint;
var c : longint;
begin
while b > 0 do begin
c := a;
a := b;
b := c mod b;
end;
DBD := a;
end;
long long DBD(long long a, long long b) {
long long c;
while (b > 0) {
c = a;
a = b;
b = c % b;
}
return a;
}
Jei reikia rasti dviejų skaičių DBD, tačiau nežinome, ar jie
teigiami, funkciją iškviečiame perduodami skaičių modulius:
DBD(abs(a), abs(b)).
Euklido algoritmas yra teisingas, nes remiasi sąryšiu:
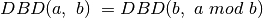 . Šio sąryšio teisingumu
nesunku įsitikinti pasinaudojus lygybe:
. Šio sąryšio teisingumu
nesunku įsitikinti pasinaudojus lygybe:

Du skaičiai turi vieną ir tik vieną didžiausiąjį bendrą daliklį.
Tarkime, 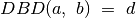 . Daliklis
. Daliklis 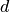 dalija skaičių
dalija skaičių
 ir taip pat dalija jo dalį
ir taip pat dalija jo dalį 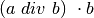 ,
todėl turi dalyti ir likusią skaičiaus
,
todėl turi dalyti ir likusią skaičiaus  dalį –
dalį –
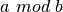 . Taigi skaičių
. Taigi skaičių  ir
ir 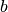 didžiausias
bendrasis daliklis yra ir (mažesnių) skaičių poros
didžiausias
bendrasis daliklis yra ir (mažesnių) skaičių poros 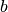 ir
ir
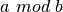 didžiausias bendrasis daliklis, t. y.
didžiausias bendrasis daliklis, t. y.
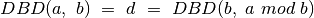 .
.
Pamėginkime įvertinti Euklido algoritmo sudėtingumą. Pasiremsime
nelygybe 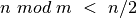 , kur
, kur  ir
ir 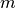 –
sveikieji neneigiami skaičiai ir
–
sveikieji neneigiami skaičiai ir 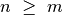 .
.
Nelygybė teisinga, nes:
jei
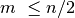 , tuomet
, tuomet 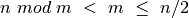 ;
;jei
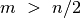 , tuomet
, tuomet  ; tada lygybę
; tada lygybę
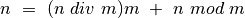 perrašome:
perrašome:
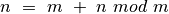 ; gauname
; gauname
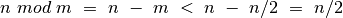 .
.
Tarkime, kad 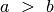 (jei taip nėra, tai atliekant ciklą
pirmąjį kartą, šie skaičiai bus sukeisti vietomis). Ciklo viduje
atliekamas operacijas galime laikyti elementariomis, tad Euklido
algoritmo sudėtingumas tiesiog proporcingas tam, kiek kartų bus
atliekamas ciklas while.
(jei taip nėra, tai atliekant ciklą
pirmąjį kartą, šie skaičiai bus sukeisti vietomis). Ciklo viduje
atliekamas operacijas galime laikyti elementariomis, tad Euklido
algoritmo sudėtingumas tiesiog proporcingas tam, kiek kartų bus
atliekamas ciklas while.
Panagrinėkime, kaip keičiasi kintamųjų  ir
ir 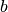 reikšmės vykdant while ciklą. Sakykime, pradinės šių kintamųjų
reikšmės yra
reikšmės vykdant while ciklą. Sakykime, pradinės šių kintamųjų
reikšmės yra 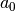 ir
ir 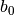 . Po pirmos ciklo iteracijos
. Po pirmos ciklo iteracijos
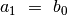 , o
, o 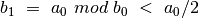 . Po
antros iteracijos
. Po
antros iteracijos 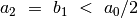 , o
, o
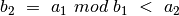 . Gavome, kad atlikus dvi ciklo
iteracijas, pirmojo kintamojo reikšmė sumažėja daugiau negu dvigubai
ir dar vis galioja
. Gavome, kad atlikus dvi ciklo
iteracijas, pirmojo kintamojo reikšmė sumažėja daugiau negu dvigubai
ir dar vis galioja 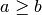 . Po keturių iteracijų pirmojo
kintamojo reikšmė bus daugiau nei keturis kartus mažesnė už
pradinę ir t. t. Taigi matyti, kad ciklas bus vykdomas ne daugiau kaip
. Po keturių iteracijų pirmojo
kintamojo reikšmė bus daugiau nei keturis kartus mažesnė už
pradinę ir t. t. Taigi matyti, kad ciklas bus vykdomas ne daugiau kaip
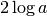 kartų. Dabar jau nesunku įvertinti, kad Euklido
algoritmo sudėtingumas yra
kartų. Dabar jau nesunku įvertinti, kad Euklido
algoritmo sudėtingumas yra 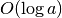 .
.
Kadangi Euklido algoritmas apibrėžiamas rekurentiniais sąryšiais:
, jei
, jei
tai Euklido algoritmą nesunku užrašyti rekursyvia 1 funkcija:
function DBD(a, b : longint) : longint;
begin
if b = 0 then
DBD := a
else
DBD := DBD(b, a mod b);
end;
long long DBD(long long a, long long b) {
return b == 0 ? a : DBD(b, a%b);
}
Pastebėkime, kad jei 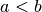 , algoritmas pirmu žingsniu šiuos
skaičius sukeičia vietomis, pavyzdžiui,
, algoritmas pirmu žingsniu šiuos
skaičius sukeičia vietomis, pavyzdžiui,
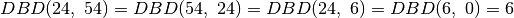 .
.
Beje, pats Euklidas šį algoritmą aprašė kiek kitaip. Mat graikų matematikai nelaikė, kad vienetas dalija kitą teigiamą skaičių. Buvo galimi trys variantai: arba du teigiami sveikieji skaičiai yra abu lygūs vienetui, arba tarpusavyje pirminiai, arba turi bendrą didžiausią daliklį. Vienetas netgi nebuvo laikomas skaičiumi, o nulis apskritai neegzistavo.
Euklido algoritmo taikymas, mažiausio bendrojo kartotinio (MBK) radimas¶
Didžiausiojo bendrojo daliklio gali prireikti sprendžiant įvairius skaičiavimo uždavinius. Vienas iš pavyzdžių – prastinant trupmenas, skaitiklį ir vardiklį reikia padalyti iš didžiausio jų bendrojo daliklio.
Euklido algoritmas leidžia efektyviai apskaičiuoti ir mažiausią bendrąjį kartotinį:
function MBK(a, b : longint) : longint;
begin
MBK := a * b div DBD(a, b);
end;
long long MBK(long long a, long long b) {
return a / DBD(a,b) * b;
}
Pastaba
Svarbu nepamiršti, kad longint tipo kintamieji gali saugoti
reikšmes, ne didesnes negu 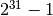 . Taigi
. Taigi 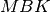 bus
skaičiuojamas teisingai tik tuo atveju, kai skaičius
bus
skaičiuojamas teisingai tik tuo atveju, kai skaičius  ir
ir
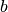 sandauga neviršija šio skaičiaus.
sandauga neviršija šio skaičiaus.
Naudodamiesi Euklido algoritmu galime rasti ne tik dviejų, bet ir
keleto skaičių 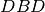 bei
bei 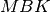 . Kadangi
. Kadangi
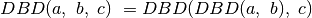 , ir
, ir
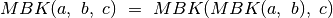 . Šias lygybes suprasti
ir įrodyti nesunku įsivaizduojant, kaip konstruotume
. Šias lygybes suprasti
ir įrodyti nesunku įsivaizduojant, kaip konstruotume 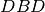 ir
ir
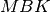 iš skaičių
iš skaičių  ,
, 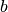 ir
ir  pirminių
daugiklių.
pirminių
daugiklių.
Tarkime, masyve 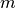 yra
yra  sveikųjų skaičių. Pateiksime
fragmentą, randantį visų
sveikųjų skaičių. Pateiksime
fragmentą, randantį visų  skaičių
skaičių 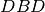 ir
ir
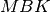 :
:
visųDBD := 0; { po pirmo žingsnio taps lygiu m[1] }
for i := 1 to k do
visųDBD := DBD(abs(m[i]), visųDBD);
int visųDBD = 0; // po pirmo žingsnio taps lygiu m[0]
for(int i = 0; i < n; i++) {
visųDBD = DBD(visųDBD, abs(m[i]));
}
visųMBK := 1; { po pirmo žingsnio taps lygiu m[1] }
for i := 1 to k do
visųMBK := MBK(abs(m[i]), visųMBK);
int visųMBK = 1; // po pirmo žingsnio taps lygiu m[0]
for(int i = 0; i < n; i++) {
visųMBK = MBK(visųMBK, abs(m[i]));
}
Išnašos