Svoriniai grafai, Trumpiausio kelio paieška – Dijkstros algoritmas¶
Most of fundamental ideas of science are essentially simple.Dauguma fundamentalių mokslo idėjų yra iš esmės paprastos.Albertas Enšteinas (Albert Einstein)
Dažnai tikslinga grafo briaunai (arba lankui) priskirti kokį nors dydį. Pavyzdžiui, jei grafu modeliuojame vietovės žemėlapį (viršūnėmis – miestus, o briaunomis – kelius), tai briaunoms galima priskirti tų kelių ilgius. Šiame skyrelyje aptarsime tokių grafų vaizdavimą ir vieną iš garsiausių algoritmų – Dijkstros algoritmą trumpiausiam keliui rasti.
Svoriniai grafai¶
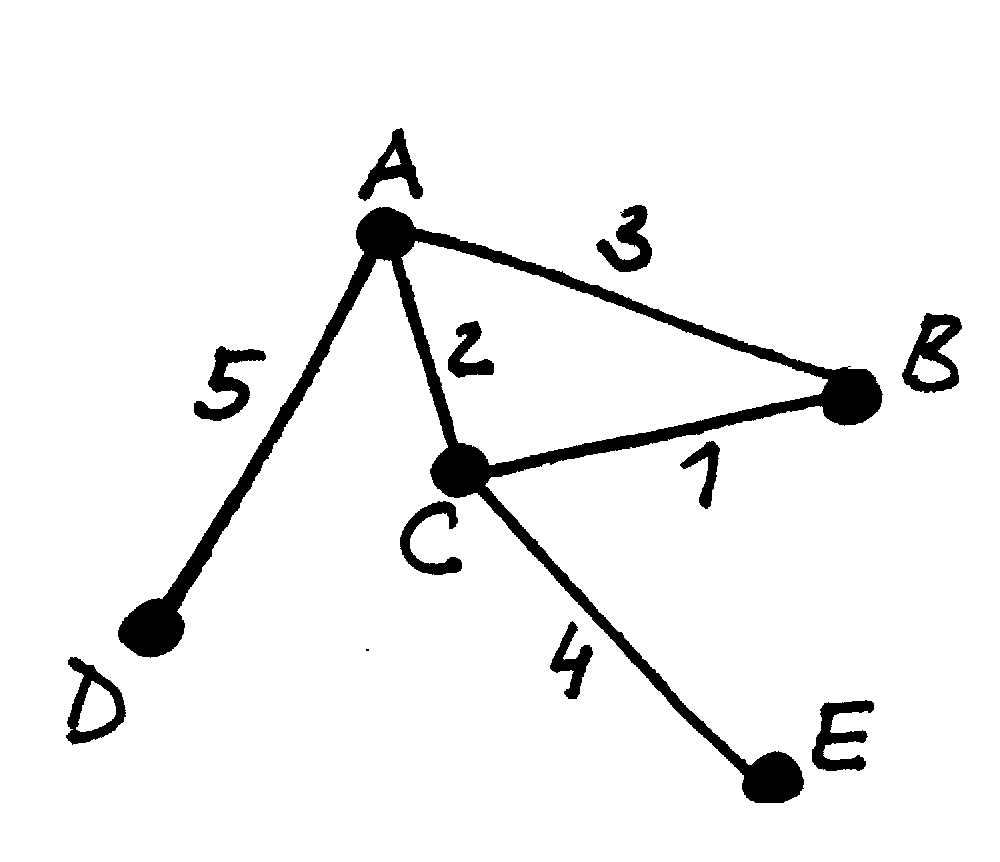
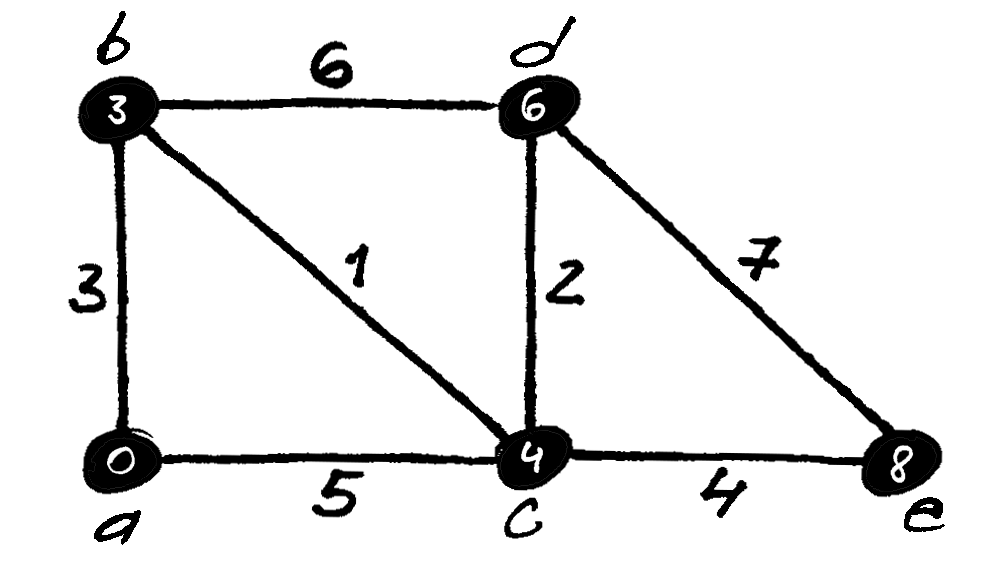
Fig. 60 Svorinio grafo pavyzdys¶
Grafas, kurio visoms briaunoms (lankams) yra priskirti dydžiai (svoriai), vadinamas svoriniu. Dažniausiai nagrinėjami svoriniai grafai, kurių briaunų svoriai yra skaičiai.
Galime tarti, kad paprastas besvoris grafas tėra atskiras svorinio grafo atvejis, kai visų briaunų svoriai lygūs 1.
Duomenų struktūra, kuria galime pavaizduoti svorinį grafą, nesudėtinga. Galime naudoti kaimynystės matricą, kurioje saugosime briaunų svorius. Ta pati matrica turėtų saugoti ne tik briaunų svorius, bet ir parodyti, kurios grafo briaunos egzistuoja, kurios ne. Neegzistuojančias briaunas galime žymėti tokiu skaičiumi, kokio svorio būti negali, pavyzdžiui „begaliniu“ (labai dideliu) svoriu arba neigiamu skaičiumi (pavyzdžiui, jei grafo svoriai reiškia atstumus tarp miestų). Bet kuriuo atveju reikia būti tikram, kad jokioje algoritmo vykdymo stadijoje egzistuojančios briaunos svoris negalės įgauti tokios reikšmės.
const MAXN = ...; { maksimalus grafo viršūnių skaičius }
BEGALINIS = MAXINT;
type grafas = record
n : integer; { viršūnių skaičius }
svoris : array [1..MAXN,
1..MAXN] of integer;
{ briaunų svorių matrica }
end;
const int MAXN = ...; // maksimalus grafo viršūnių skaičius
const int BEGALINIS = ...;
/*
Konstanta BEGALINIS - kažkoks pakankamai didelis skaičius, kuris turėtų būti didesnis už bet
kokį įmanomą atstumą, tad atstotų begalybės reikšmę. Pavyzdžiui, dažnai naudojama reikšmė 1e9.
*/
int n; // viršūnių skaičius
int svoris[MAXN][MAXN];
Šitaip vaizduojant grafą, viršūnes 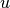 ir
ir  jungia
briauna, jei
jungia
briauna, jei G.svoris[u, v] < BEGALINIS.
Jei grafas vaizduojamas kaimynystės sąrašais, tai briaunos svorį tenka arba saugoti atskirame dvimačiame masyve, arba kiekvienai viršūnei sudaryti iš jos išeinančių briaunų svorių sąrašą.
Trumpiausio kelio paieškos algoritmas – Dijkstros algoritmas¶
Nagrinėjant olimpiadinių uždavinių sprendimus dažnai gali tekti susidurti su Dijkstros algoritmu trumpiausio kelio grafe paieškai. Šio algoritmo autorius – E. V. Dijkstra (Edsger Wybe Dijkstra) – olandų mokslininkas, daug nusipelnęs kompiuterių mokslui, ypač programavimo kalbų srityje. Trumpiausio kelio algoritmas nėra svarbiausias jo darbas, tačiau daugelis Dijkstros pavardę sieja būtent su šiuo algoritmu.

Fig. 61 E. V. Dijsktra (Edsger Wybe Dijkstra) 1930–2002¶
Pats E. V. Dijkstra apie tai rašo: „Daug metų plačiuose sluoksniuose trumpiausio kelio algoritmas garsino mano vardą ir teikė šlovės, tačiau nuostabu tai, kad jis buvo sukurtas net be popieriaus ir pieštuko, geriant kavą su žmona saulėtoje Amsterdamo kavinės terasoje, sukurtas tik pademonstruoti kompiuterio galimybėms…“
Jau esame aptarę vieną algoritmą, tinkamą trumpiausio kelio
paieškai – paiešką platyn. Pradėta viršūnėje 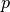 ,
paieška platyn pirmiau ima viršūnes, kurių atstumas nuo viršūnės
,
paieška platyn pirmiau ima viršūnes, kurių atstumas nuo viršūnės
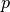 (matuojamas briaunų, kuriomis einama, skaičiumi) yra
mažiausias.
(matuojamas briaunų, kuriomis einama, skaičiumi) yra
mažiausias.
Nagrinėkime svorinį grafą 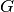 , kurio briaunos
, kurio briaunos 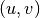 svoris reiškia atstumą tarp viršūnių
svoris reiškia atstumą tarp viršūnių 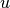 ir
ir  .
Kelio svoriniame grafe ilgiu vadinsime visų kelią sudarančių
briaunų svorių sumą. Nagrinėsime svorinį grafą
.
Kelio svoriniame grafe ilgiu vadinsime visų kelią sudarančių
briaunų svorių sumą. Nagrinėsime svorinį grafą 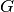 , kurio
briaunos
, kurio
briaunos 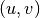 neneigiamas svoris reiškia atstumą tarp
viršūnių
neneigiamas svoris reiškia atstumą tarp
viršūnių 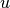 ir
ir  . Kaip ieškoti trumpiausio kelio
tokiame grafe? Nesunku įsitikinti, kad paieška platyn čia visai
netinkamas algoritmas, kadangi trumpiausias kelias nebūtinai reikš
mažiausią briaunų, kuriomis einama, skaičių (pavyzdžiui, pasiekti
viršūnę einant dviem briaunomis, kurių svoriai atitinkamai, 1 ir 2,
yra „pigiau“ negu viena briauna, kurios svoris 5, nes
. Kaip ieškoti trumpiausio kelio
tokiame grafe? Nesunku įsitikinti, kad paieška platyn čia visai
netinkamas algoritmas, kadangi trumpiausias kelias nebūtinai reikš
mažiausią briaunų, kuriomis einama, skaičių (pavyzdžiui, pasiekti
viršūnę einant dviem briaunomis, kurių svoriai atitinkamai, 1 ir 2,
yra „pigiau“ negu viena briauna, kurios svoris 5, nes
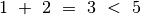 ).
).
Dijkstros algoritmas, kaip ir paieška platyn, iš duotosios viršūnės
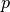 randa trumpiausius kelius iki visų svorinio grafo
viršūnių. Algoritmas skirsto viršūnes į dvi aibes: tų, iki kurių
trumpiausi keliai (ir atstumai) jau žinomi (jas vadinsime
prijungtomis), ir visų kitų.
randa trumpiausius kelius iki visų svorinio grafo
viršūnių. Algoritmas skirsto viršūnes į dvi aibes: tų, iki kurių
trumpiausi keliai (ir atstumai) jau žinomi (jas vadinsime
prijungtomis), ir visų kitų.
Pradžioje nežinomas trumpiausias kelias nė iki vienos viršūnės,
išskyrus pradinę 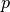 , tad pažymima, kad atstumai iki šių
viršūnių yra begaliniai. Atstumas (nuo pradinės) iki pradinės
viršūnės jau žinomas – jis lygus nuliui.
, tad pažymima, kad atstumai iki šių
viršūnių yra begaliniai. Atstumas (nuo pradinės) iki pradinės
viršūnės jau žinomas – jis lygus nuliui.
Kiekvienu žingsniu algoritmas suranda dar neprijungtą viršūnę,
iki kurios atstumas yra mažiausias (pirmu algoritmo žingsniu tai
pradinė viršūnė 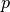 , kadangi iki visų kitų viršūnių
atstumai yra begaliniai). Pasirinktoji viršūnė prijungiama, o tuomet
atnaujinama informacija apie visas neprijungtas jos kaimynes: galbūt
kelias iki šios viršūnės dar nebuvo rastas, o jei buvo – tai
galbūt kelias, einantis per ką tik prijungtąją viršūnę iki šios
kaimynės, yra trumpesnis už iki šiol rastąjį.
, kadangi iki visų kitų viršūnių
atstumai yra begaliniai). Pasirinktoji viršūnė prijungiama, o tuomet
atnaujinama informacija apie visas neprijungtas jos kaimynes: galbūt
kelias iki šios viršūnės dar nebuvo rastas, o jei buvo – tai
galbūt kelias, einantis per ką tik prijungtąją viršūnę iki šios
kaimynės, yra trumpesnis už iki šiol rastąjį.
Taigi pirmuoju algoritmo žingsniu prijungiama pradinė viršūnė
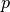 . Antruoju – artimiausia
. Antruoju – artimiausia 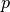 kaimynė. Kiekvienu
žingsniu prijungiamų viršūnių atstumai sudaro nemažėjančią
seką, kadangi visąlaik bandoma prijungti kuo artimesnes viršūnes.
Šie samprotavimai intuityviai pagrindžia algoritmo teisingumą.
Prijungdami viršūnę, galime būti tikri, jog rastasis atstumas yra
trumpiausias, kadangi visi kiti, vėliau atrasti, trumpiausi atstumai
bus tik ilgesni už šį.
kaimynė. Kiekvienu
žingsniu prijungiamų viršūnių atstumai sudaro nemažėjančią
seką, kadangi visąlaik bandoma prijungti kuo artimesnes viršūnes.
Šie samprotavimai intuityviai pagrindžia algoritmo teisingumą.
Prijungdami viršūnę, galime būti tikri, jog rastasis atstumas yra
trumpiausias, kadangi visi kiti, vėliau atrasti, trumpiausi atstumai
bus tik ilgesni už šį.
Kadangi ieškoma trumpiausių kelių, o ne tik jų ilgių, kiekvienai
viršūnei išsaugoma jos pirminė viršūnė (tai viršūnė, iš
kurios į ją ateinama einant trumpiausiu keliu). Kol kelias iki
viršūnės nerastas, jos pirminė viršūnė yra neapibrėžta.
Atnaujinant atstumą iki viršūnės, kartu pažymima, iš kurios
viršūnės į ją ateinama. Algoritmo vykdymo metu kiekvienos
viršūnės pirminė viršūnė (kaip ir trumpiausias rastas atstumas)
gali ne kartą pasikeisti. Dijkstros algoritmo vykdymas konkrečiame
grafe, kai ieškomi trumpiausi keliai iš viršūnės  iki
kitų grafo viršūnių.
iki
kitų grafo viršūnių.
Pradinė situacija: trumpiausio kelio iki viršūnės
|
|
Viršūnė |
|
Iš neprijungtų viršūnių išrenkama ta, iki
kurios atstumas trumpiausias (viršūnę |
|
Baigus vykdyti Dijkstros algoritmą visos
viršūnės yra prijungtos (t. y. visos yra
pasiekiamos iš pradinės viršūnės) ir žinomi
trumpiausi atstumai iki jų: trumpiausio kelio iki
viršūnės |
Toliau pateikiamas algoritmo tekstas, tinkamas trumpiausių kelių paieškai tiek orientuotame, tiek ir neorientuotame grafe. Grafas vaizduojamas kaimynystės matrica.
type masyvas = array [1..MAXN] of longint;
logmas = array [1..MAXN] of boolean;
procedure dijkstra(var G : grafas;
var atstumas, pirminė : masyvas;
p : integer);
var prijungta : logmas;
v, u : integer;
min : longint;
begin
{ įrašomos pradinės masyvų reikšmės }
for u := 1 to G.n do begin
atstumas[u] := BEGALINIS;
pirminė[u] := -1;
prijungta[u] := false;
end;
atstumas[p] := 0;
v := p;
while v <> 0 do begin
{ jei v <> 0, tai rasta viršūnė, kurią galima prijungti }
prijungta[v] := true;
for u := 1 to G.n do { peržiūrimos kaimynės }
if (G.svoris[v, u] < BEGALINIS) and
(atstumas[u] >
atstumas[v] + G.svoris[v, u])
then begin { į viršūnę u verčiau eiti per v }
atstumas[u] :=
atstumas[v] + G.svoris[v, u];
pirminė[u] := v;
end;
{ randama tolesnė kandidatė -
dar neprijungta viršūnė su mažiausiu atstumu }
v := 0;
min := BEGALINIS;
for u := 1 to G.n do
if not prijungta[u] and
(atstumas[u] < min)
then begin
v := u;
min := atstumas[u];
end;
{ jei jokia viršūnė nerasta, tai v = 0 ir ciklas nutraukiamas }
end;
end;
Kodas analogiškas Paskalio kalba užrašytam variantui:
int atstumas[MAXN];
int pirmine[MAXN];
bool prijungta[MAXN];
void dijkstra (int p) {
// įrašomos pradinės masyvų reikšmės
for (int u = 0; u < n; u++) {
atstumas[u] = BEGALINIS;
pirmine[u] = -1;
prijungta[u] = false;
}
atstumas[p] = 0;
int v = p;
while (v != -1) {
// jei v != -1, tai rasta viršūnė, kurią galima prijungti
prijungta[v] = true;
for (int u = 0; u < n; u++) {
if (svoris[v][u] < BEGALINIS && atstumas[u] > atstumas[v] + svoris[v][u]) {
// į viršūnę u verčiau eiti per v
atstumas[u] = atstumas[v] + svoris[v][u];
pirmine[u] = v;
}
}
// randama tolesnė viršūnė - dar neprijungta viršūnė su mažiausiu atstumu
v = -1;
int minAtstumas = BEGALINIS;
for (int u = 0; u < n; u++) {
if (!prijungta[u] && atstumas[u] < minAtstumas) {
v = u;
minAtstumas = atstumas[u];
}
}
// jei tokia viršūnė nerasta, tai v = -1 ir ciklas nutraukiamas
}
}
Dijkstros algoritmo realizacija panaudojant priority_queue:
vector<pair<int, int>> adj[MAXN];
/*
adj[i] yra i-tosios viršūnės kaimynų sąrašas, kur
adj[i][j].first yra j-tosios kaimynės numeris
adj[i][j].second yra briaunos, jungiančios i-tąją viršūnę su jos j-tąja kaimyne, svoris
*/
void dijkstra (int p) {
// įrašomos pradinės masyvų reikšmės
for (int u = 0; u < n; u++) {
atstumas[u] = BEGALINIS;
pirmine[u] = -1;
prijungta[u] = false;
}
atstumas[p] = 0;
priority_queue<pair<int, int>, vector<pair<int,int>>, greater<pair<int,int>>> q; // priority_queue, kurios top() elementas visad yra mažiausias
q.push({atstumas[p], p}); // į q visados dedam poras {atstumas[i], i}, nes tada q.top() elementas visad būs mažiausio atstumo
while (!q.empty()) {
int v = q.top().second;
if (!prijungta[v]) {
prijungta[v] = true;
for (auto p : adj[v]) { // einame per viršūnės v kaimynus
int u = p.first; // kaimynės numeris
int w = p.second; // briaunos tarp v ir u svoris
if (atstumas[u] > atstumas[v] + w) {
// verčiau į u eiti per v
atstumas[u] = atstumas[v] + w;
pirmine[u] = v;
q.push ({atstumas[u], u});
}
}
}
}
}
Užrašytojo algoritmo sudėtingumas yra 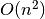 , kur
, kur  – grafo viršūnių skaičius. Pasitelkus sudėtingesnes duomenų
struktūras, Dijkstros algoritmą galima pagreitinti iki
– grafo viršūnių skaičius. Pasitelkus sudėtingesnes duomenų
struktūras, Dijkstros algoritmą galima pagreitinti iki
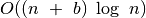 (čia
(čia 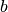 – grafo briaunų
skaičius). Pastarasis sudėtingumas yra kur kas geresnis retuose
(turinčiuose nedaug briaunų) grafuose.
– grafo briaunų
skaičius). Pastarasis sudėtingumas yra kur kas geresnis retuose
(turinčiuose nedaug briaunų) grafuose.
Uždavinys Aplink žemę per 80 dienų 1¶
Žiulio Verno knygoje pasakojama, kaip Filijas Fogas apkeliavo aplink Žemę per 80 dienų. Tačiau galbūt sudarius labai gerą maršrutą, jam būtų pasisekę apkeliauti dar greičiau.
Žinomi įvairių transporto priemonių, vykstančių į rytus (Filijas Fogas keliavo tik į rytus), tvarkaraščiai, tie patys visomis dienomis. Apie kiekvieną reisą žinoma šitokia informacija: išvykimo miestas, išvykimo laikas, miestai, kuriuose sustojama, kelionės trukmė tarp dviejų gretimų stočių. Visi tvarkaraščiai nurodyti Grinvičo laiku.
Laikomasi susitarimo, kad tarpinėje stotyje transporto priemonės neužsibūna: atvyksta ir išvyksta tą pačią minutę, taip pat kad persėsti iš vienos transporto priemonės į kitą galima tą pačią minutę.
Užduotis. Žinomas miestas, iš kurio pradedama keliauti. Kelionės pradžia yra lygiai vidurnaktis Grinvičo laiku. Parašykite programą, kuria nustatytumėte, ar galima apkeliauti aplink Žemės rutulį pagal pateiktus susisiekimo priemonių tvarkaraščius ir, jei galima, informuotumėte, kada anksčiausiai įmanoma grįžti į miestą, iš kurio buvo išvykta.
Kaip jau galėjote atspėti, uždavinys bus sprendžiamas taikant Dijkstros algoritmą. Tačiau olimpiada nėra kontrolinis darbas, kuriuo tikrinama, ar gerai dalyviai moka vieną ar kitą algoritmą. Tad ir uždaviniai olimpiadose pateikiami tokie, kad net žinant algoritmą, tenka jį modifikuoti ir pritaikyti neįprastai situacijai.
Sudarysime orientuotą grafą, kurio viršūnės atitiks miestus. Reikia
rasti trumpiausią kelią iš pradinio miesto atgal į jį patį, tik
trumpiausią laiko prasme. Tačiau Dijkstros algoritmas kiekvieną
viršūnę nagrinėja tik po vieną kartą, todėl pradinį miestą (į
kurį turime sugrįžti) pavaizduosime dviem viršūnėmis (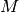 ir
ir
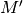 ): viena turės tik išeinančius lankus, kita – tik
įeinančius.
): viena turės tik išeinančius lankus, kita – tik
įeinančius.
Galime būti tikri, kad bet kuri kelionė iš viršūnės 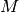 į
viršūnę
į
viršūnę 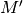 bus kelionė aplink pasaulį, kadangi visi
maršrutai yra tik rytų krypties.
bus kelionė aplink pasaulį, kadangi visi
maršrutai yra tik rytų krypties.
Į bet kurį maršrutą galima žiūrėti kaip į kelių tiesioginių (be persėdimų) ir nepriklausomų reisų rinkinį. Kiekvieną tokį (tiesioginį) reisą grafe atitiktų lankas, turintis du parametrus (svorius): reiso pradžios laiką ir jo trukmę. Kiekvienu Dijkstros algoritmo žingsniu būtų prijungiama viršūnė, iki kurios galime atvykti anksčiausiai. Prijungus viršūnę peržiūrimi visi iš jos išeinantys lankai. Pagal atvykimo į šią viršūnę laiką ir maršruto trukmę apskaičiuojama, kada galima nuvykti į kaimynines viršūnes.
Panagrinėkime pavyzdį. Sakykime, duoti 7 miestai, Filijas Fogas kelionę pradeda ir baigia antrajame, ir galimi tokie maršrutai:
Pirmasis maršrutas: 2 → 5 → 6, išvykimo laikas – 5:35, važiavimų trukmės: 2:44 ir 21:07.
Antrasis maršrutas: 3 → 5 → 1 → 6, išvykimo laikas – 7:16, važiavimų trukmės: 1:14, 7:10, 3:40.
Trečiasis maršrutas: 4 → 6 → 7 → 2, išvykimo laikas – 3:20, važiavimų trukmės: 1:00, 15:40, 1:15.
Ketvirtasis maršrutas: 6 → 4 → 3 → 2, išvykimo laikas – 19:30, važiavimų trukmės: 0:20, 1:00, 0:35.
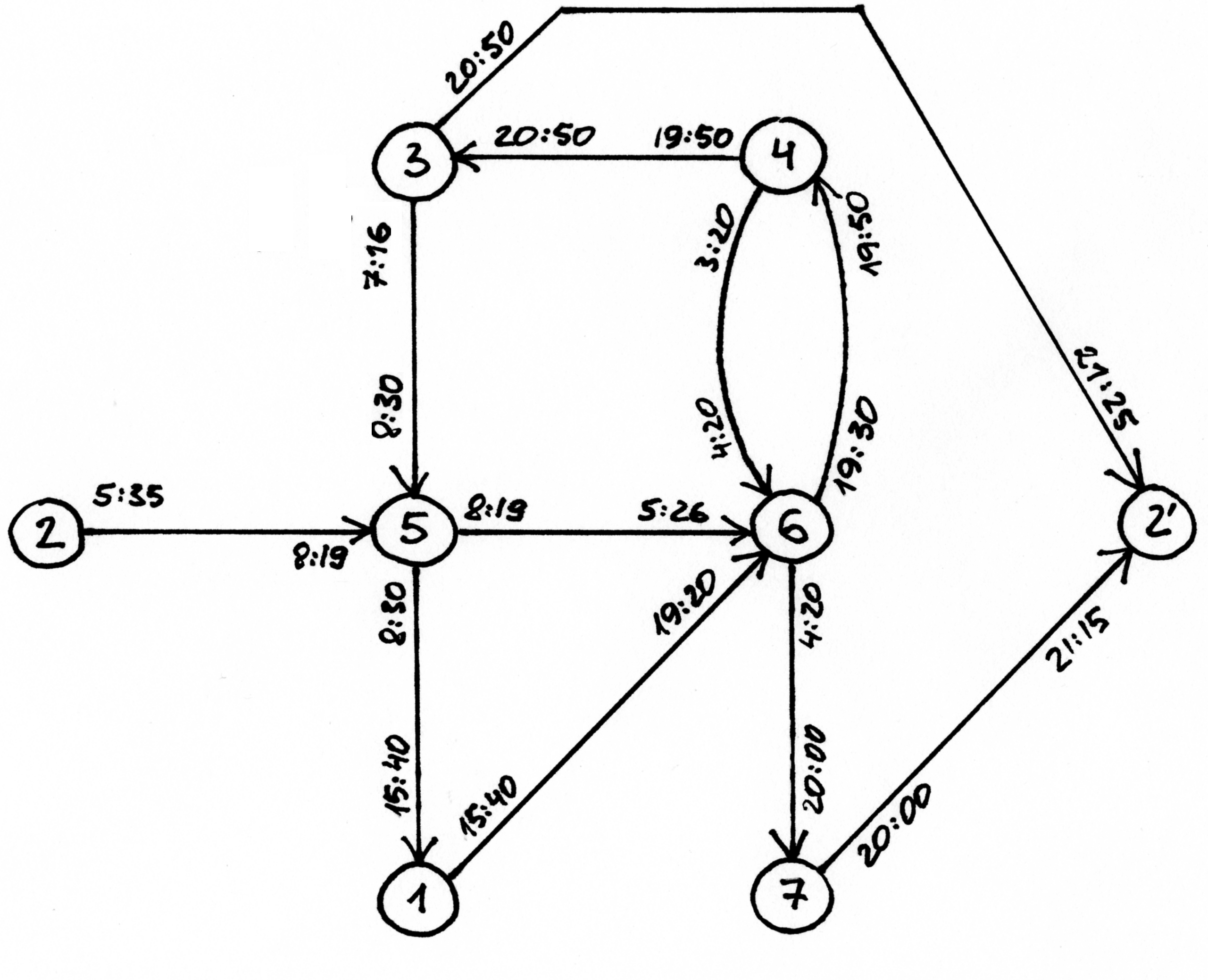
Fig. 62 Pavyzdyje pateiktus maršrutus atitinkantis grafas; kad iliustracija būtų aiškesnė, vietoj važiavimo trukmių nurodyti atvykimo laikai (nė vienas reisas netrunka ilgiau nei parą)¶
Šiuos maršrutus atitinkantis grafas pateiktas Fig. 62 paveiksle. Tarkime, Filijas Fogas pradeda kelionę iš antrojo miesto. Jis anksčiausiai sugrįš namo, jei stotyje lauks iki ryto ir 5:35 išvyks į penktąjį miestą (tai, beje, vienintelis reisas iš antrojo miesto). Penktajame mieste jam verta persėsti ir važiuoti į pirmąjį miestą, o iš ten – į šeštąjį, kuriame jis atsidurs 19 val. 20 min. Ir spės į reisą, išvykstantį į ketvirtąjį miestą 19 val. 30 min. O iš ten be persėdimo važiuos iki pradinio miesto. Kelionės trukmė: 21 val. 25 min.
Jeigu Filijas Fogas penktajame mieste nepersėstų ir važiuotų toliau į šeštąjį miestą, tuomet jis ten atsidurtų kitos dienos ryte: 5 val. 26 min. ir pavėluotų į rytinį reisą, vykstantį į septintą miestą. Jam tektų laukti iki vakaro ir tik 19 val. 30 min. jis galėtų išvykti į ketvirtąjį miestą. Kelionė aplink pasaulį truktų 1 parą, 21 val. ir 25 min., t. y. lygiai parą ilgiau nei optimaliu atveju.
Kadangi gali būti keli skirtingi reisai tarp tų pačių miestų, grafą būtina vaizduoti kaimynystės sąrašais. Sutarsime, kad skaitant pradinius duomenis, visi tarpinių sustojimų turintys maršrutai iš karto išskaidomi į persėdimų neturinčius reisus ir tuo pačiu sudaromas grafas. Taip pat sutarsime, kad, kuriant grafą, išvykimo laikai perskaičiuoti minutėmis. Rezultatas (laikas, kada anksčiausiai įmanoma grįžti) taip pat pateikiamas minutėmis nuo kelionės pradžios.
const BEGALINIS = MAXLONGINT;
PARA = 24 * 60;
MAXM = ...; { maksimalus miestų skaičius }
MAXR = ...; { maksimalus reisų skaičius }
type masyvas = array [1..MAXM + 1] of longint;
logmas = array [1..MAXM + 1] of boolean;
reisas = record
kur, kada, trukmė : longint;
end;
reisai_iš_miesto = record
k : longint; { reisų skaičius }
reisai : array [1..MAXR] of reisas;
end;
grafas = record
n : longint; { miestų skaičius }
mst : array [1..MAXM+1] of reisai_iš_miesto;
end;
procedure dijkstra(var G : grafas;
pr : longint; { pradinis miestas }
var laikas : masyvas {atvykimo laikai});
var i, u, v, t, min, atvykta, išvyksta : longint;
prijungta : logmas;
begin
{ įrašomos pradinės masyvų reikšmės }
for u := 1 to G.n do begin
laikas[u] := BEGALINIS;
prijungta[u] := false;
end;
laikas[pr] := 0;
v := pr;
while v <> 0 do begin
{ prijungiama viršūnė v }
prijungta[v] := true;
{ atnaujinama informacija apie kaimynes }
for i := 1 to G.mst[v].k do begin
u := G.mst[v].reisai[i].kur;
t := G.mst[v].reisai[i].trukmė;
{ kiek reikės laukti mieste v ? }
atvykta := laikas[v] mod PARA;
išvyksta := G.mst[v].reisai[i].kada;
if atvykta <= išvyksta then
{ reisu pavyks išvykti tą pačią parą }
t := t + (išvyksta - atvykta)
else { teks laukti kitos dienos }
t := t + (PARA - atvykta) + išvyksta;
{ ar į u verta vykti per v? }
if laikas[u] > laikas[v] + t then
laikas[u] := laikas[v] + t;
end;
{ randama tolesnė kandidatė –
dar neprijungta viršūnė su mažiausiu atstumu }
v := 0;
min := BEGALINIS;
for u := 1 to G.n do
if not prijungta[u] and (laikas[u] < min)
then begin
v := u;
min := laikas[u];
end;
end;
end;
procedure keliauk(var G : grafas; { informacija apie visus
reisus iš kiekvieno miesto}
pr : longint; { pradinis miestas}
var atvykimas : longint { sprendinys});
var i, j, pb : longint;
laikas : masyvas;
begin
{ pradinis miestas keičiams dviem miestais: miestu, kuriame
kelionė prasidėjo ir fiktyviu, kuriame kelionė baigėsi }
G.n := G.n + 1;
pb := G.n;
for i := 1 to G.n - 1 do
for j := 1 to g.mst[i].k do
if G.mst[i].reisai[j].kur = pr then
G.mst[i].reisai[j].kur := pb;
{ suskaičiuojama, per kokį mažiausią laiką galima
nuvykti į kiekvieną miestą }
dijkstra(G, pr, laikas);
atvykimas := laikas[pb];
{ jei maršruto nėra, atvykimas = BEGALINIS }
end;
const long long BEGALINIS = 1e18;
const long long PARA = 24*60;
const int MAXM = ...; // maksimalus miestų skaičius
const int MAXR = ...; // maksimalus reisų skaičius
struct reisas {
int kur, kada, trukme;
};
struct reisaiIsMiesto {
int k; // miestų skaičius
reisas reisai[MAXR];
};
int n; // miestų skaičius
reisaiIsMiesto mst[MAXM]; // grafas
long long laikas[MAXM]; // atvykimo laikai
bool prijungta[MAXM];
void dijkstra (int pr) { // pr - pradinis miestas
// įrašomos pradinės masyvų reikšmės
for (int u = 0; u < n; u++) {
laikas[u] = BEGALINIS;
prijungta[u] = false;
}
laikas[pr] = 0;
int v = pr;
while (v != -1) {
// prijungiama viršūnė v
prijungta[v] = true;
// atnaujinama informacija apie kaimynes
for (int i = 0; i < mst[v].k; i++) {
int u = mst[v].reisai[i].kur;
int t = mst[v].reisai[i].trukme;
// kiek reikės laukti mieste u?
int atvyksta = laikas[v] % PARA;
int isvyksta = mst[v].reisai[i].kada;
if (atvyksta <= isvyksta) // reisu pavyks išvykti tą pačią dieną
t += (isvyksta - atvyksta);
else // teks laukti kitos dienos
t += (PARA - atvyksta) + isvyksta;
// ar į u verta vykti per v?
if (laikas[u] > laikas[v] + t)
laikas[u] = laikas[v] + t;
}
// randama tolesnė kandidatė - dar neprijungta viršūnė su mažiausiu atstumu
v = -1;
int minAtstumas = BEGALINIS;
for (int u = 0; u < n; u++) {
if (!prijungta[u] && laikas[u] < minAtstumas) {
v = u;
minAtstumas = laikas[u];
}
}
}
}
void keliauk (int pr) { // pr - pradinis miestas
/*
pradinis miestas keičiamas dviem miestais:
miestu, kuriame kelionė prasidėjo, ir
fiktyviu, kuriame kelionė baigėsi
*/
int pb = n;
n++;
for (int i = 0; i < n-1; i++)
for (int j = 0; j < mst[i].k; j++)
if (mst[i].reisai[j].kur == pr)
mst[i].reisai[j].kut = pb;
// suskaičiuojama, per kokį mažiausią laiką galima nuvykti į kiekvieną miestą
dijkstra (pr);
return laikas[pb];
// jei maršruto nėra - laikas[pb] yra BEGALINIS
}
Išnašos
- 1
Panašus uždavinys buvo pateiktas Lietuvos moksleivių informatikos olimpiadoje III etape 2000 metais.
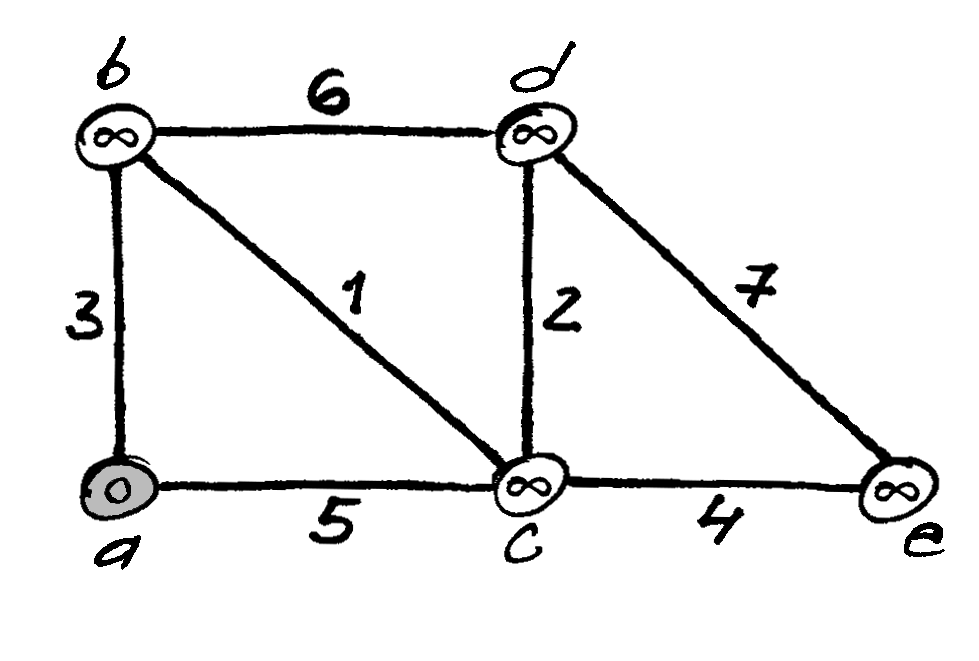
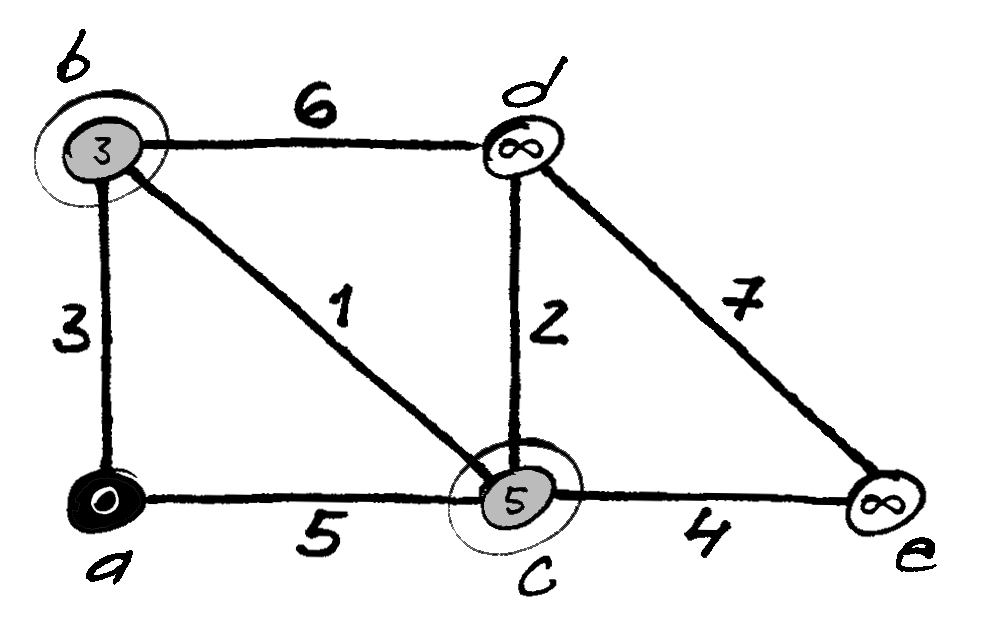
 ; iki šių viršūnių rasti trumpesni keliai
; iki šių viršūnių rasti trumpesni keliai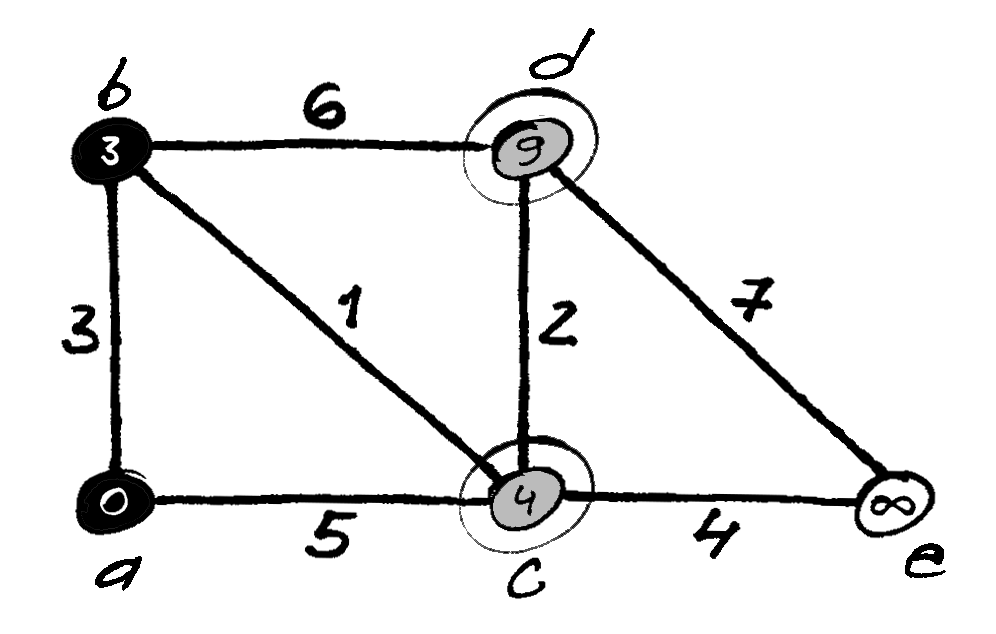
 ir pastebima, kad
iki šių abiejų viršūnių rasti trumpesni keliai
per viršūnę
ir pastebima, kad
iki šių abiejų viršūnių rasti trumpesni keliai
per viršūnę 

 – 8.
– 8.