Pirminiai skaičiai¶
Matematikai veltui bandė atrasti kokį nors dėsningumą pirminiųskaičių sekoje, ir yra priežasčių manyti, kad šios paslaptiesžmogaus protas neperpras niekada.Leonardas Oileris (Leonhard Euler)
Manoma, kad pirminiai skaičiai buvo žinomi jau Babilonijos civilizacijoje. Nuo seniausių laikų jie domino matematikus. XX a. pabaigoje pirminiai skaičiai buvo sėkmingai pritaikyti kriptografijoje: kelios populiarios viešojo rakto kriptoschemos paremtos faktu, jog sudauginti du skaičius lengva, o didelį skaičių išskaidyti pirminiais daugikliais – labai sudėtinga. Žinių apie pirminius skaičius gali prireikti ir sprendžiant įvairius skaičiavimo uždavinius.
Pirminiai skaičiai ir pagrindinė aritmetikos teorema¶
Pirminiais vadinami natūralieji skaičiai, kurie dalijasi tik iš vieneto ir savęs. Štai dešimt pirmųjų pirminių skaičių: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Pirminiai skaičiai matematikoje yra svarbūs dėl pagrindinės aritmetikos teoremos, teigiančios, kad kiekvieną skaičių vieninteliu (unikaliu) būdu galima išreikšti pirminių skaičių sandauga, nekreipiant dėmesio į jų tvarką. Didelė šios teoremos svarba yra viena priežasčių, kodėl skaičius vienas nelaikomas pirminiu: tuomet teoremą reikėtų papildyti dar viena nereikalinga sąlyga.
Kiek jų yra?¶
Pirminių skaičių yra be galo daug. Tai žmonės žinojo jau labai seniai. Euklidas savo veikale „Pradmenys“ pateikė grakštų įrodymą:
Tarkime, kad pirminių skaičių yra baigtinis kiekis –
. Pažymėkime šiuos
pirminių skaičių
, ir panagrinėkime skaičių
. Dalydami
iš bet kurio
(
) gausime liekaną 1, t. y. nė vienas pirminis skaičius nedalija
. Tai reiškia, kad arba
pats yra pirminis, arba išrašėme ne visus pirminius skaičius. Bet kuriuo atveju yra bent
pirminių skaičių – gavome prieštarą. Taigi pradžioje padaryta prielaida, kad pirminių skaičių yra baigtinis kiekis, buvo neteisinga. Vadinasi, pirminių skaičių yra be galo daug. Tai ir reikėjo įrodyti.
Kiek yra pirminių skaičių, ne didesnių už  ? Šis klausimas
buvo užduodamas taip dažnai, kad atsakymas turi net specialų vardą
–
? Šis klausimas
buvo užduodamas taip dažnai, kad atsakymas turi net specialų vardą
– 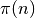 . Pi funkcijos reikšmė lygi pirminių skaičių,
mažesnių arba lygių
. Pi funkcijos reikšmė lygi pirminių skaičių,
mažesnių arba lygių  , skaičiui (ši funkcija neturi nieko
bendra su skaičiumi
, skaičiui (ši funkcija neturi nieko
bendra su skaičiumi 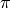 ). Pavyzdžiui,
). Pavyzdžiui, 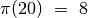 ,
nes yra aštuoni pirminiai skaičiai, mažesni arba lygūs 20. Iš
tiesų nėra jokio paprasto ir efektyvaus būdo, kaip šią funkciją
apskaičiuoti, kai argumentas didelis 1.
,
nes yra aštuoni pirminiai skaičiai, mažesni arba lygūs 20. Iš
tiesų nėra jokio paprasto ir efektyvaus būdo, kaip šią funkciją
apskaičiuoti, kai argumentas didelis 1.
Ar skaičius 234234743 pirminis?¶
Pats paprasčiausias būdas nustatyti, ar skaičius  pirminis
– patikrinti, ar jis tenkina pirminio skaičiaus apibrėžimą, t. y.
ar neatsiras tokio skaičiaus
pirminis
– patikrinti, ar jis tenkina pirminio skaičiaus apibrėžimą, t. y.
ar neatsiras tokio skaičiaus 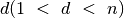 , kuris dalytų
, kuris dalytų
 . Algoritmo, tikrinančio visus potencialius daliklius nuo
. Algoritmo, tikrinančio visus potencialius daliklius nuo
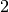 iki
iki 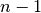 , sudėtingumas yra
, sudėtingumas yra 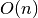 .
.
Veiksmų skaičių nesunku sumažinti dvigubai: iš pradžių
patikrinę, ar  nelyginis, vėliau galime tikrinti dalumą tik
iš nelyginių skaičių. Nors veiksmų teks atlikti beveik dvigubai
mažiau, algoritmo sudėtingumas taip pat yra
nelyginis, vėliau galime tikrinti dalumą tik
iš nelyginių skaičių. Nors veiksmų teks atlikti beveik dvigubai
mažiau, algoritmo sudėtingumas taip pat yra 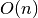 , nes veiksmų
skaičius tiesiškai priklauso nuo
, nes veiksmų
skaičius tiesiškai priklauso nuo  . Įrodysime, kad pakanka
tikrinti potencialius daliklius nuo 2 iki
. Įrodysime, kad pakanka
tikrinti potencialius daliklius nuo 2 iki 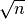 .
.
Tarkime,
. Jei
ir
, tuomet
, taigi arba
, arba
. Todėl, nuosekliai ieškodami daliklių nuo 2, negalime tikėtis rasti daliklį
, nes
taip pat turi būti skaičiaus
daliklis, ir jį mes būtume aptikę anksčiau.
Apibendrinę šiuos pastebėjimus, galime parašyti pakankamai spartų
(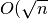 ) sudėtingumo) algoritmą, tikrinantį, ar skaičius
) sudėtingumo) algoritmą, tikrinantį, ar skaičius
 pirminis.
pirminis.
function pirminis(n : longint) : boolean;
var d, { potencialus daliklis }
sn : longint; { riba, iki kurios ieškosime daliklių }
begin
pirminis := (n mod 2 <> 0) or (n = 2);
sn := round(sqrt(n) + 1);
d := 3; { tikrinsime dalumą iš nelyginių skaičių }
while pirminis and (d < sn) do
if n mod d = 0 then pirminis := false
else d := d + 2;
end;
bool pirminis(long long n) {
if(n == 1) return false;
if(n == 2) return true;
if(n%2 == 0) return false;
for(int d = 3; d*d <= n; d+=2) {
if(n%d == 0) return false;
}
return true;
}
Įvykdę funkciją pirminis galime atsakyti į skyrelio pradžioje
pateiktą klausimą – skaičius 234234743 tikrai pirminis.
Jei skaičių reikšmės būtų per didelės standartiniams sveikųjų skaičių tipams, tai su jais atliekamos aritmetinės operacijos nebegalėtų būti prilyginamos elementariems veiksmams, o joms atlikti tektų rašyti specialias procedūras. Tai keistų ir algoritmo sudėtingumą.
Ilgą laiką buvo nežinomas polinominis algoritmas, tikrinantis, ar didelis skaičius yra pirminis 2, ir tik 2002 metais Indijos mokslininkų grupė įrodė, kad tai nėra NP pilnas uždavinys. Beje, jei būtų atrastas būdas efektyviai išskaidyti didelį skaičių pirminiais dauginamaisiais, tai kai kurios svarbios saugumo sistemos taptų nesaugios.
Eratosteno rėtis¶
Jei norėtume surasti visus pirminius skaičius, mažesnius arba lygius
 , galėtume tikrinti kiekvieną iš jų ką tik aprašytuoju
būdu. Tokio algoritmo sudėtingumas –
, galėtume tikrinti kiekvieną iš jų ką tik aprašytuoju
būdu. Tokio algoritmo sudėtingumas – 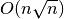 .
Tačiau šitaip ieškodami pirminių skaičių mes nepasinaudotume
svarbiu faktu: tikrinant, ar skaičius
.
Tačiau šitaip ieškodami pirminių skaičių mes nepasinaudotume
svarbiu faktu: tikrinant, ar skaičius 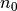 pirminis, jau rasti
visi pirminiai skaičiai, mažesni už
pirminis, jau rasti
visi pirminiai skaičiai, mažesni už 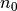 .
.
Geresnį pirminių skaičių paieškos algoritmą prieš kelis tūkstančius metų sugalvojo graikų matematikas Eratostenas (graikų k. Ἐρατοσθένης). Graikijoje tuo metu buvo rašoma ant papiruso arba odos, o vykdant šį algoritmą, sudėtinis skaičius buvo išbraukiamas jį perduriant aštria lazdele. Pabaigus vykdyti algoritmą, lentelė primindavo rėtį, todėl šis algoritmas vadinamas Eratosteno rėčiu.
Surašykime visus skaičius nuo 1 iki  į eilę. Skaičių
„sijojimas“ vyksta labai paprastai: eile keliaujama nuo 2 iki
į eilę. Skaičių
„sijojimas“ vyksta labai paprastai: eile keliaujama nuo 2 iki
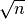 , ir, sutikus neišbrauktą skaičių
, ir, sutikus neišbrauktą skaičių  ,
išbraukiami visi
,
išbraukiami visi  kartotiniai iki
kartotiniai iki  (išskyrus patį
skaičių
(išskyrus patį
skaičių  ). Tokiu būdu „atsijojami“ sudėtiniai
skaičiai, o visi likę yra pirminiai (išskyrus, žinoma, vienetą).
). Tokiu būdu „atsijojami“ sudėtiniai
skaičiai, o visi likę yra pirminiai (išskyrus, žinoma, vienetą).
Naudodamiesi Eratosteno rėčiu raskime visus pirminius skaičius, ne
didesnius kaip 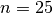 .
.
Į eilę surašome skaičius nuo 1 iki 25, o eile keliausime iki
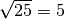 .
.

Pradedame nuo skaičiaus 2 – patį skaičių paliekame, o visus jo kartotinius išbraukiame.

Paeiname eile per vieną skaičių į dešinę (nuo 2 pereiname prie 3). 3 neišbrauktas, tad 3 paliekame, o visus kartotinius išbraukiame.
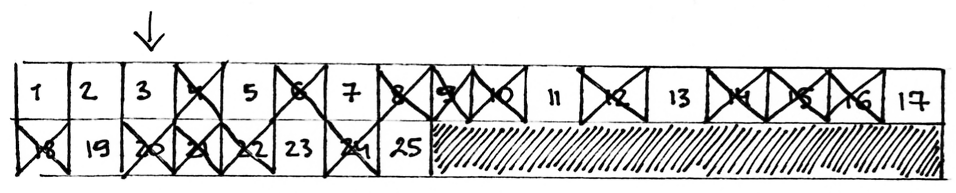
Vėl pereiname per vieną skaičių į dešinę. Skaičius 4 jau išbrauktas, tačiau 5 – ne. Išbraukiame visus skaičiaus 5 kartotinius:
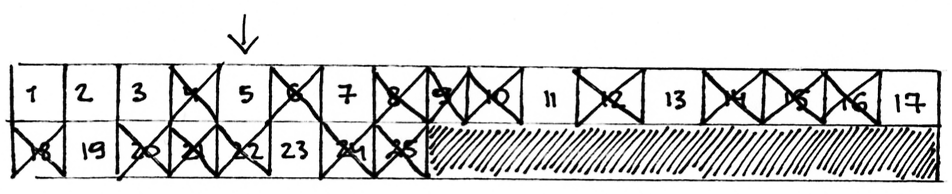
Pasiekėme 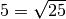 , taigi darbą baigiame. Eilėje liko
pirminiai skaičiai, ne didesni už 25, ir vienetas.
, taigi darbą baigiame. Eilėje liko
pirminiai skaičiai, ne didesni už 25, ir vienetas.
Dabar užrašykime algoritmą Paskalio kalba. Skaičių eilę vaizduosime loginiu masyvu pirm.
for k := 2 to n do
pirm[k] := true;
for k := 2 to round(sqrt(n) + 1) do
if pirm[k] then begin
j := 2 * k;
while (j <= n) do begin
pirm[j] := false;
j := j + k;
end;
end;
std::vector<bool> arPirminis(MAXN, true);
arPirminis.at(0) = false;
arPirminis.at(1) = false;
for(int i = 2; i*i <= n; i++) {
if(arPirminis[i]) {
for(int j = 2*i; j <= n; j+=i) {
arPirminis[j] = false;
}
}
}
Šis algoritmas reikalauja 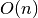 atminties (loginiam masyvui).
Turbūt ne taip akivaizdu, kad algoritmas reikalauja
atminties (loginiam masyvui).
Turbūt ne taip akivaizdu, kad algoritmas reikalauja
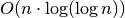 laiko – šio fakto neįrodinėsime.
Iš tiesų algoritmo sudėtingumas beveik tiesinis.
laiko – šio fakto neįrodinėsime.
Iš tiesų algoritmo sudėtingumas beveik tiesinis.
Kartą įvykdę Eratosteno rėčio algoritmą, galime per konstantinį
(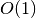 ) laiką patikrinti, ar skaičius iš intervalo
) laiką patikrinti, ar skaičius iš intervalo
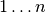 yra pirminis, – tereikia patikrinti atitinkamą
masyvo elementą.
yra pirminis, – tereikia patikrinti atitinkamą
masyvo elementą.
Abu aptartus algoritmus galima naudoti kartu. Įsivaizduokime, jog tenka
tikrinti, ar dideli skaičiai (iki 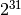 ) yra pirminiai. Tiek
atminties skirti negalime, todėl negalime naudoti Eratosteno rėčio
algoritmo. Tačiau Eratosteno rėčiu suradę visus pirminius skaičius
iki
) yra pirminiai. Tiek
atminties skirti negalime, todėl negalime naudoti Eratosteno rėčio
algoritmo. Tačiau Eratosteno rėčiu suradę visus pirminius skaičius
iki 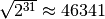 ir perkėlę į atskirą
masyvą, juos galime naudoti kaip potencialius daliklius vietoj visų
skaičių iš intervalo
ir perkėlę į atskirą
masyvą, juos galime naudoti kaip potencialius daliklius vietoj visų
skaičių iš intervalo 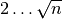 .
.
Tarkime, visi pirminiai skaičiai iki 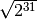 iš eilės
surašyti masyve
iš eilės
surašyti masyve p. Tuomet ankstesnę patikrinimo, ar skaičius
pirminis, funkciją galime pakeisti spartesne:
function pirminis(n : longint) : boolean;
var i, { masyvo p indeksas }
sn : longint; { riba, iki kurios ieškosime daliklių }
begin
pirminis := true;
sn := round(sqrt(n) + 1);
i := 1;
while pirminis and (p[i] < sn) do
if n mod p[i] = 0 then
pirminis := false
else
i := i + 1;
end;
vector<int> primes; // visi pirminiai skaiciai iki sqrt(n)
bool pirminis(long long n) {
for(int i = 0; primes[i]*primes[i] <= n; i++) {
if(n%primes[i] == 0) return false;
}
return true;
}
Pirminių skaičių paieška tęsiasi¶

Fig. 6 Marinas Mersenas (1588–1648)¶

Fig. 7 1963 m. didžiausio tuo metu žinomo pirminio skaičiaus garbei buvo skirtas pašto ženklas¶
Pirminių skaičių yra be galo daug, tad didžiausio jų ir negali
būti. Nuo senų laikų lenktyniaujama, kas atras didesnį pirminį
skaičių. XVII amžiuje matematikai ėmė intensyviai ieškoti
dėsningumų pirminių skaičių sekoje. Tuo metu gyvenęs filosofas ir
matematikas vienuolis Marinas Mersenas (Marin Mersenne) pastebėjo,
kad daug skaičių, užrašomų pavidalu 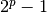 , kur
, kur 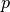 – pirminis skaičius, taip pat yra pirminiai. Tokie pirminiai
skaičiai dabar vadinami Merseno pirminiais. Atsiradus kompiuteriams,
šie iš karto buvo pasitelkti pirminių skaičių paieškai. 1997
metais pirminių skaičių paieškai buvo sukurtas GIMPS (angl. The
Great Internet Mersenne Prime Search) paskirstytų skaičiavimų
projektas. Visi norintys dalyvauti šiame projekte gali atsisiųsti į
savo kompiuterį programinę įrangą, kuri išnaudos laisvą jūsų
kompiuterio procesoriaus darbo laiką: parsisiųs ir atliks tam tikrą
užduočių paketą, o rezultatus perduos į centrinį serverį. Šio
projekto vykdytojai jau rado net 9 didžiausius (tuo metu) Merseno
pirminius skaičius. 1999 m. EFF (Electronic Frontier Foundation)
paskelbė šimtatūkstantines premijas pirmiesiems, atradusiems
pirminius skaičius, turinčius labai daug (nuo
– pirminis skaičius, taip pat yra pirminiai. Tokie pirminiai
skaičiai dabar vadinami Merseno pirminiais. Atsiradus kompiuteriams,
šie iš karto buvo pasitelkti pirminių skaičių paieškai. 1997
metais pirminių skaičių paieškai buvo sukurtas GIMPS (angl. The
Great Internet Mersenne Prime Search) paskirstytų skaičiavimų
projektas. Visi norintys dalyvauti šiame projekte gali atsisiųsti į
savo kompiuterį programinę įrangą, kuri išnaudos laisvą jūsų
kompiuterio procesoriaus darbo laiką: parsisiųs ir atliks tam tikrą
užduočių paketą, o rezultatus perduos į centrinį serverį. Šio
projekto vykdytojai jau rado net 9 didžiausius (tuo metu) Merseno
pirminius skaičius. 1999 m. EFF (Electronic Frontier Foundation)
paskelbė šimtatūkstantines premijas pirmiesiems, atradusiems
pirminius skaičius, turinčius labai daug (nuo 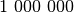 )
skaitmenų. Pirmoji 50 000 dolerių premija jau buvo išmokėta 2000
metais GIMPS projekto dalyviui, atradusiam Merseno pirminį, sudarytą
iš
)
skaitmenų. Pirmoji 50 000 dolerių premija jau buvo išmokėta 2000
metais GIMPS projekto dalyviui, atradusiam Merseno pirminį, sudarytą
iš 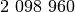 skaitmenų. 2005 gruodžio 15 dieną buvo
atrastas 43-iasis Merseno pirminis skaičius
skaitmenų. 2005 gruodžio 15 dieną buvo
atrastas 43-iasis Merseno pirminis skaičius 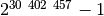 ,
sudarytas iš
,
sudarytas iš 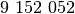 skaitmenų. Tad iki antrosios,
dvigubai didesnės, premijos už iš ne mažiau kaip
skaitmenų. Tad iki antrosios,
dvigubai didesnės, premijos už iš ne mažiau kaip
 skaitmenų sudarytą pirminį skaičių laukti
lieka neilgai.
skaitmenų sudarytą pirminį skaičių laukti
lieka neilgai.
Išnašos
- 1
Tačiau įrodyta, jog teisingas šis funkcijos vertinimas:
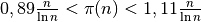 .
Taigi funkcijos
.
Taigi funkcijos 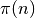 priklausomybė nuo argumento nedaug
skiriasi nuo tiesinės.
priklausomybė nuo argumento nedaug
skiriasi nuo tiesinės.- 2
Operacijų su dideliais skaičiais sudėtingumas matuojamas aritmetinių bitų operacijų skaičiumi. Tokiu atveju pradinių duomenų dydis yra skaitmenų (bitų) skaičius, taigi skaičiui
 pradinių duomenų dydis yra
pradinių duomenų dydis yra 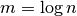 . O
algoritmas skaičiui
. O
algoritmas skaičiui  atliekantis
atliekantis  veiksmų, iš
tiesų atliks eksponentinį veiksmų skaičių, kaip funkciją nuo
pradinių duomenų dydžio:
veiksmų, iš
tiesų atliks eksponentinį veiksmų skaičių, kaip funkciją nuo
pradinių duomenų dydžio: 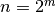 .
.
