Rikiavimas ir paieška¶
Any inaccuracies in this index may be explained by the fact that it hasbeen sorted with the help of a computerBet kokie netikslumai šiame sąraše gali būti paaiškinti tuo,kad jis buvo išrikiuotas kompiuteriu.Donaldas Knutas (Donald Knuth)
Su rikiavimo ir paieškos uždaviniais susiduriama labai dažnai. Rikiavimas ir paieška neretai yra sudėtinė kitų algoritmų dalis. Norint sėkmingai dalyvauti informatikos olimpiadose, būtina išmanyti rikiavimo ir paieškos algoritmus. Su jais susipažinsime šiame skyrelyje.
Rikiavimo uždavinys¶
Rikiavimo uždavinys apibrėžiamas taip: reikia rasti tokią sekos
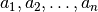 perstatą
perstatą
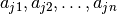 , kad
, kad
 .
.
Praktikoje retai rikiuojama vien tik skaičių seka. Dažniausiai dirbama su sudėtingesniais duomenimis (įrašais), kurie rikiuojami pagal vieną ar kelis įrašo laukus. Pastaruoju atveju norint palyginti du įrašus tenka apibrėžti, kada vienas įrašas „mažesnis“ už kitą, ir parašyti atskirą loginę funkciją dviems elementams palyginti.
Kad nekomplikuotume, algoritmus pateiksime rikiuodami skaičių masyvą didėjimo (nemažėjimo) tvarka:
const MAXN = ...; { maksimalus masyvo ilgis }
type masyvas = array [1..MAXN] of integer;
const int MAXN = ...;
int a[MAXN];
Rikiavimo algoritmų yra daug ir įvairių, tolesniuose skyreliuose aptarsime tik kelis naudingiausius. Pateiktus algoritmus bus nesunku pritaikyti ir kitokiems duomenų tipams.
Rikiavimas įterpimu¶
Rikiavimo įterpimu (angl. Insertion sort) algoritmo idėja primena rankoje laikomų kortų rikiavimą – į išrikiuotų kortų eilę kiekvienu žingsniu įterpiama viena nauja korta.

Fig. 20 Rikiavimo įterpimu pavyzdys¶
Pradedant rikiuoti masyvą, surikiuota masyvo dalis susideda iš vieno
(pirmojo) elemento. Prieš atliekant  -ąjį žingsnį, jau yra
išrikiuota masyvo dalis
-ąjį žingsnį, jau yra
išrikiuota masyvo dalis ![[1..k]](_images/math/b0ab41f0ff702227899c171d1e693044e66b0d27.png) , o
, o  -uoju žingsniu
-uoju žingsniu
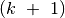 -asis elementas įterpiamas į šią išrikiuotą
dalį. Įterpimas atliekamas tokiu būdu:
-asis elementas įterpiamas į šią išrikiuotą
dalį. Įterpimas atliekamas tokiu būdu: 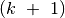 -asis
elementas įsimenamas, visi didesni už jį išrikiuotos masyvo dalies
elementai paslenkami pirmyn, o šis įterpiamas į naują savo vietą.
-asis
elementas įsimenamas, visi didesni už jį išrikiuotos masyvo dalies
elementai paslenkami pirmyn, o šis įterpiamas į naują savo vietą.
procedure rikiuok(const n : integer;
var A : masyvas);
var i, k, t : integer;
begin
for k := 1 to n - 1 do begin
t := A[k + 1];
{ skaičių t įterpsime į išrikiuotą masyvo dalį [1..k] }
i := k;
while (i > 0) and (A[i] > t) do begin
A[i + 1] := A[i];
i := i - 1;
end;
A[i + 1] := t;
end;
end;
/*
Pastaba: kintamasis n ir masyvas a aprašytas globaliai
praeitame kodo pavyzdyje.
*/
void rikiuok () {
for (int k = 0; k < n-1; k++) {
int t = a[k+1];
// Skaičių t terprsime į išrikiuotą masyvo dalį [1..k]
int i = k;
while (i > 0 && a[i] > t) {
a[i+1] = a[i];
i--;
}
a[i+1] = t;
}
}
Algoritmo sudėtingumas blogiausiu atveju yra 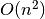 . Tuo
nesunku įsitikinti panagrinėjus algoritmo veikimą rikiuojant seką,
kuri jau išrikiuota priešinga tvarka – tuomet kiekvienu žingsniu
elementas įterpiamas į masyvo pradžią. Taigi atliekamų veiksmų
skaičius priklauso nuo pradinės masyvo tvarkos. Kuo tvarkingesnis
(panašesnis į išrikiuotą) yra masyvas, tuo greičiau veikia
rikiavimas įterpimu. Jei tenka rikiuoti beveik išrikiuotą masyvą,
algoritmas veikia beveik tiesiškai.
. Tuo
nesunku įsitikinti panagrinėjus algoritmo veikimą rikiuojant seką,
kuri jau išrikiuota priešinga tvarka – tuomet kiekvienu žingsniu
elementas įterpiamas į masyvo pradžią. Taigi atliekamų veiksmų
skaičius priklauso nuo pradinės masyvo tvarkos. Kuo tvarkingesnis
(panašesnis į išrikiuotą) yra masyvas, tuo greičiau veikia
rikiavimas įterpimu. Jei tenka rikiuoti beveik išrikiuotą masyvą,
algoritmas veikia beveik tiesiškai.
Algoritmas nėra tinkamas rikiuoti didelių elementų masyvams, kadangi atliekama itin daug kopijavimo operacijų. Tačiau rikiavimą įterpimu efektyvu taikyti sąrašų (sudėtingesnių duomenų struktūrų) rikiavimui – juose elemento įterpimą galima atlikti nekopijuojant kitų elementų.
Taigi rikiavimą įterpimu verta naudoti, jei masyvas nedidelis, jame saugomi nedideli elementai arba iš anksto žinoma, kad teks kelis kartus rikiuoti tą patį masyvą, pavyzdžiui, pakeitus kelis jo elementus.
Greitasis rikiavimas¶
Greitojo rikiavimo algoritmas (angl. Quicksort) perskiria rikiuojamą masyvą į dvi dalis, ir kiekvieną dalį išrikiuoja atskirai. Pagalvokime, kokias sąlygas turi tenkinti masyvas, kad perskyrę jį pusiau ir šias dalis išrikiavę atskirai, gautume išrikiuotą masyvą. Atsakymas gana paprastas: pirmojoje dalyje turi būti mažesnieji elementai, o antroje – didesnieji, t.y. pirmoje dalyje neturi būti jokio elemento, kuris, išrikiavus masyvą, atsidurtų antroje dalyje ir atvirkščiai.
Deja, nežinomas joks greitas (tiesinis) „perkėlimo“ algoritmas. Tačiau nenusiminkime. Yra žinomi tiesinio sudėtingumo algoritmai, kurie, perkeldami mažesniuosius elementus į pirmą dalies pusę, padalija masyvą beveik pusiau. T. y. tikimybė, kad padalijimas bus neblogas (abiejose pusėse elementų skaičius bus panašus), yra labai didelė.
Pateiksime funkciją perskirk, perskiriančią masyvo dalį
![[k..d]](_images/math/bece940206db7076289e39508ce82a8db5eaf752.png) į dvi dalis
į dvi dalis ![[k..v]](_images/math/3b5437ecfb6cda830c60b2f7ef095489700548b2.png) ir
ir ![[v+1..d]](_images/math/e7e641fafcca29192e270c7e87bf31a9d1140d8e.png) taip, kad
pirmojoje dalyje atsidurtų mažesnieji elementai, o antroje –
didesnieji. Kadangi funkcija ne visuomet masyvo dalį perskiria pusiau,
ji grąžina dalijamojo elemento indeksą v (t. y. vietą, kurioje
masyvo dalis perskiriama). Šios informacijos reikia rikiavimo
algoritmui.
taip, kad
pirmojoje dalyje atsidurtų mažesnieji elementai, o antroje –
didesnieji. Kadangi funkcija ne visuomet masyvo dalį perskiria pusiau,
ji grąžina dalijamojo elemento indeksą v (t. y. vietą, kurioje
masyvo dalis perskiriama). Šios informacijos reikia rikiavimo
algoritmui.
function perskirk(var A : masyvas;
const k, d : integer) : integer;
procedure sukeisk(var x, y : integer);
var t : integer;
begin
t := x;
x := y;
y := t;
end;
var x : integer; { dalijamoji reikšmė }
i, j : integer;
begin
x := A[k];
i := k - 1;
j := d + 1;
perskirk := 0;
while perskirk = 0 do begin { dalis dar neperskirta }
repeat { praleidžiami elementai, mažesni už x }
i := i + 1
until A[i] >= x;
repeat { praleidžiami elementai, didesni už x }
j := j - 1
until A[j] <= x;
if i < j then sukeisk(A[i], A[j])
else perskirk := j;
end;
end;
/*
Pastaba: masyvas a aprašytas globaliai
viename iš praeitų kodo pavyzdžių.
*/
int perskirk (int k, int d) {
int x = a[k]; // dalijamoji reikšmė
int i = k-1;
int j = d+1;
int rez = 0; // grąžinamas rezultatas
while (rez == 0) {
do { // praleidžiami elementai, mažesni už x
i++;
} while (a[i] >= x);
do { // praleidžiami elementai, didesni už x
j--;
} while (a[i] <= x);
if (i < j)
swap(a[i], a[j]);
else
rez = j;
}
return rez;
}
Šis perskyrimo algoritmas pirmiausia pasirenka dalijamąją reikšmę
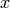 ir pamažu augina dvi masyvo dalis:
ir pamažu augina dvi masyvo dalis: ![[k..i]](_images/math/4cf69c1825a8de242dc2f787a6faf1ec5e9bfd1e.png) su
mažesniais už
su
mažesniais už 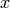 elementais ir
elementais ir ![[j..d]](_images/math/e39972e62828751bd70f178e918cad725d56b3b9.png) su elementais,
didesniais už
su elementais,
didesniais už 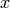 . Kai indeksai
. Kai indeksai 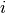 ir
ir 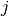 „susitinka“, algoritmas baigia darbą, o funkcija grąžina
perskyrimo vietą. Iš tiesų šioje funkcijoje slepiasi daug svarbių
detalių ir ją programuoti reikia labai atidžiai.
„susitinka“, algoritmas baigia darbą, o funkcija grąžina
perskyrimo vietą. Iš tiesų šioje funkcijoje slepiasi daug svarbių
detalių ir ją programuoti reikia labai atidžiai.
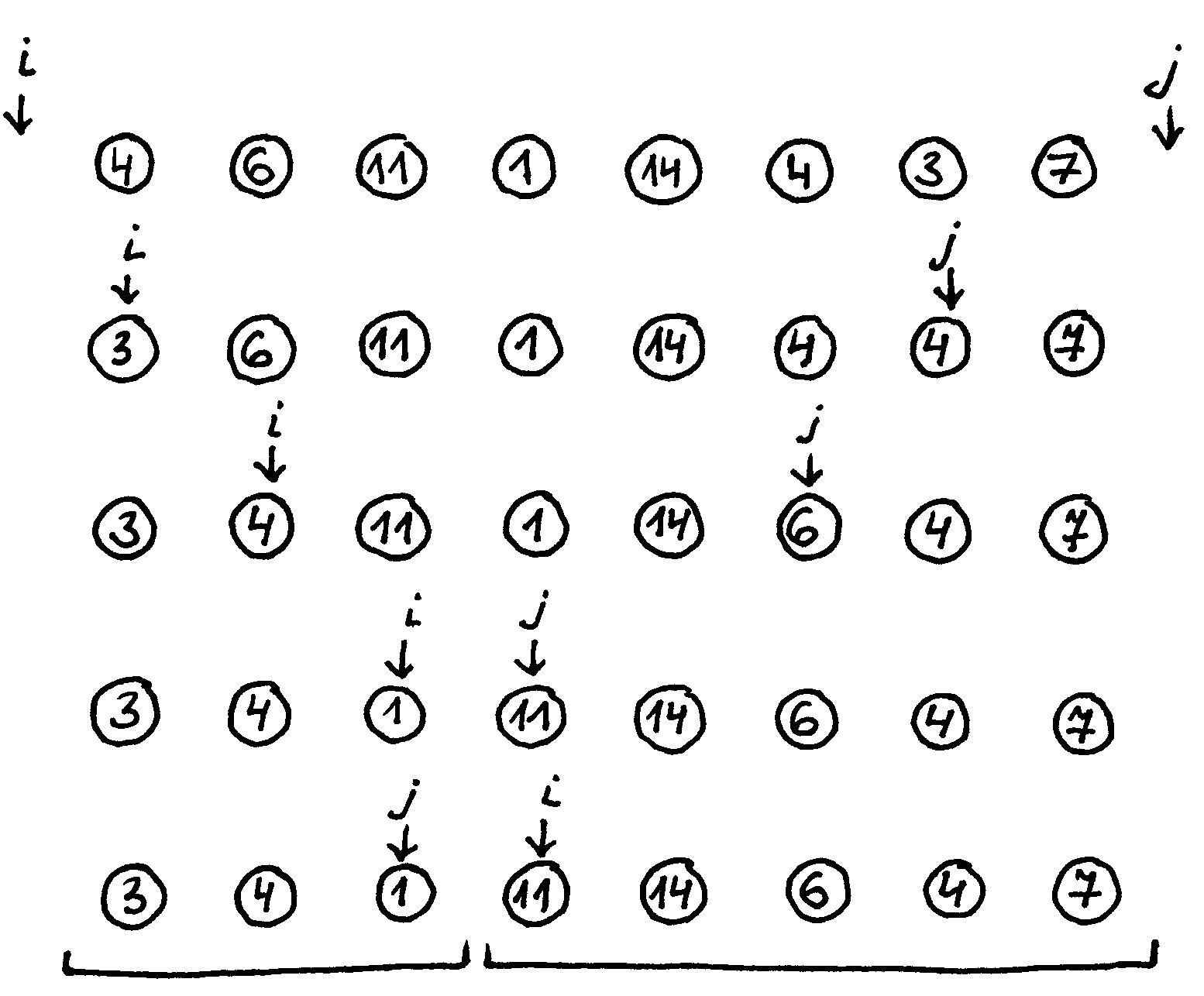
Fig. 21 Funkcijos perskirk veikimo pavyzdys¶
Dabar nesunku užrašyti greitojo rikiavimo algoritmą:
procedure rikiuok(var A : masyvas;
const k, d : integer);
var v : integer;
begin
if k < d then begin
v := perskirk(A, k, d);
{ rekursyviai išrikiuojamos kairioji ir dešinioji masyvo dalys }
rikiuok(A, k, v);
rikiuok(A, v + 1, d);
end;
end;
Norint surikiuoti  elementų seką
elementų seką 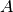 , į procedūrą
kreipiamasi
, į procedūrą
kreipiamasi rikiuok (A, 1, n);
/*
Pastaba: kintamasis n ir masyvas a aprašytas globaliai
viename iš praeitų kodo pavyzdžių.
*/
void rikiuok (int k, int d) {
if (k < d) {
int v = perskirk(k, d);
// rekursyviai išrikiuojamos kairioji ir dešinioji masyvo dalys
rikiuok (k, v);
rikiuok (v+1, d);
}
}
// Norint surikiuoti n elementų seką a, kviečiama funkcija: rikiuok (0, n-1);

Fig. 22 Greitojo rikiavimo veikimo iliustracija¶
Nelengva apskaičiuoti greitojo rikiavimo algoritmo sudėtingumą, nes
atliekamų veiksmų skaičius priklauso ne tik nuo duomenų skaičiaus,
bet ir nuo pačių duomenų. Greitojo rikiavimo algoritmo sudėtingumas
blogiausiu atveju yra 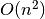 , o vidutiniu –
, o vidutiniu –
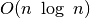 .
.
Nors yra rikiavimo algoritmų, net blogiausiu atveju išrikiuojančių
 elementų per
elementų per 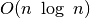 laiką, greitasis
rikiavimas, nepaisant savo blogiausio atvejo sudėtingumo, praktiškai
yra sparčiausias rikiavimo algoritmas. Be to, jį užrašyti procedūra
nesudėtinga, o jo vykdymui nereikalinga papildoma atmintis.
laiką, greitasis
rikiavimas, nepaisant savo blogiausio atvejo sudėtingumo, praktiškai
yra sparčiausias rikiavimo algoritmas. Be to, jį užrašyti procedūra
nesudėtinga, o jo vykdymui nereikalinga papildoma atmintis.
Dėl išvardytų privalumų greitasis rikiavimas dažnai naudojamas praktikoje.
Ir įterpimo, ir greitojo rikiavimo algoritmai pagrįsti dviejų
elementų palyginimais, t. y. šių algoritmų sudėtingumas
proporcingas atliekamų palyginimų skaičiui. Yra įrodyta, kad
nepavyks parašyti palyginimais paremto algoritmo, kurio efektyvumas
būtų geresnis nei 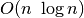 , kur
, kur  – rikiuojamos
sekos elementų skaičius. Tačiau duomenims, pasižymintiems tam
tikromis savybėmis, galima sudaryti greitesnių rikiavimo algoritmų.
Vienas tokių – rikiavimas skaičiavimu.
– rikiuojamos
sekos elementų skaičius. Tačiau duomenims, pasižymintiems tam
tikromis savybėmis, galima sudaryti greitesnių rikiavimo algoritmų.
Vienas tokių – rikiavimas skaičiavimu.
Rikiavimas skaičiavimu¶

Fig. 23 Rikiavimas skaičiavimu¶
Rikiavimas skaičiavimu (angl. Counting sort) skirtas rikiuoti sekoms, kurių visi elementai priklauso nedidelei aibei.
Pavyzdžiui, žinome, kad visi masyvo 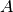 elementai yra sveikieji
skaičiai, priklausantys intervalui
elementai yra sveikieji
skaičiai, priklausantys intervalui ![[1, 1000]](_images/math/2b85cf91a249572eea813642baca4741b6061cbe.png) . Tuomet atskirame
1000 elementų skaičių masyve
. Tuomet atskirame
1000 elementų skaičių masyve 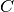 įsimenama, kiek kartų
kiekviena reikšmė pasirodo pradiniame masyve
įsimenama, kiek kartų
kiekviena reikšmė pasirodo pradiniame masyve 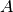 . Belieka
pasinaudoti šia informacija ir elementus surašyti atgal į masyvą
. Belieka
pasinaudoti šia informacija ir elementus surašyti atgal į masyvą
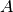 didėjimo tvarka. Šio algoritmo sudėtingumas yra
didėjimo tvarka. Šio algoritmo sudėtingumas yra
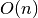 (tiesinis), o jam reikalinga papildoma atmintis priklauso
nuo aibės, kuriai priklauso rikiuojamo masyvo elementai, dydžio.
(tiesinis), o jam reikalinga papildoma atmintis priklauso
nuo aibės, kuriai priklauso rikiuojamo masyvo elementai, dydžio.
const MAXN = ...; { maksimalus masyvo ilgis }
type skaičius = 1..1000;
masyvas = array [1..MAXN] of skaičius;
intMasyvas = array [skaičius] of integer;
procedure rikiuok(const n : integer;
var A : masyvas);
var c : intMasyvas;
i, j : longint;
begin
{ suskaičiuojama, kiek kokių elementų yra masyve A }
for i := low(C) to high(C) do
C[i] := 0;
for i := 1 to n do
C[A[i]] := C[A[i]] + 1;
{ visi n masyvo A elementų surašomi iš eilės }
j := low(C);
for i := 1 to n do begin
while C[j] = 0 do
j := j + 1;
C[j] := C[j] - 1;
A[i] := j;
end;
end;
const int MAXN = ...; // maksimalus masyvo ilgis
const int MAXS = ...; // maksimali sekos nario reikšmė
int n;
int a[MAXN];
int c[MAXS+1]; // c[i] nurodys, kiek sekoje yra skaičių i
void rikiuok () {
// suskaičiuojama, kiek kokių elementų yra masyve a
for (int i = 0; i <= MAXS; i++)
c[i] = 0;
for (int i = 0; i < n; i++)
c[a[i]]++;
// visi n masyvo a elementų surašomi iš eilės
int j = 0;
for (int i = 0; i < n; i++) {
while (c[j] == 0) {
j++;
}
c[j]--;
a[i] = j;
}
}
Paieškos uždavinys¶
Paieškos uždavinys apibrėžiamas taip: duota seka
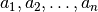 ir elementas
ir elementas 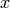 . Reikia nustatyti,
ar
. Reikia nustatyti,
ar 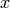 yra šioje sekoje, o jei yra, tai koks jo numeris. Kitaip
sakant, reikia rasti tokį sekos nario indeksą
yra šioje sekoje, o jei yra, tai koks jo numeris. Kitaip
sakant, reikia rasti tokį sekos nario indeksą 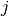 , kad būtų
, kad būtų
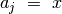 , arba nustatyti, kad
, arba nustatyti, kad 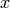 nėra lygus nė vienam
iš sekos narių.
nėra lygus nė vienam
iš sekos narių.
Praktikoje sekos nariai yra sudėtingi duomenų tipai (įrašai), o paieška atliekama pagal vieną arba kelis įrašo laukus, vadinamus paieškos raktu. Paprastumo dėlei paiešką atliksime tik skaičių sekoje, kurią vaizduosime vienmačiu masyvu.
Tiesinė paieška¶
Paprasčiausias paieškos algoritmas – iš eilės patikrinti visus
masyvo elementus – vadinamas tiesine paieška (angl. Linear
search). Patikrinimą, ar  ilgio masyve
ilgio masyve 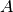 yra
elementas
yra
elementas 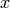 , atlieka tokia funkcija:
, atlieka tokia funkcija:
function ieškok (const n, x: integer;
var A: masyvas): integer;
var j: integer;
begin
j := 1;
while (A[j] <> x) and (j < n) do
j := j + 1;
if A[j] = x then
ieškok := j
else
ieškok := 0; { elementas nerastas }
end;
const int MAXN = ...; // maksimalus sekos ilgis
int n, x;
int a[MAXN];
int ieskok () {
for (int i = 0; i < n; i++)
if (a[i] == x)
return i;
return -1; // elementas nerastas
}
Baigus vykdyti tiesinę paiešką, funkcijos reikšmė bus lygi ieškomo
elemento indeksui masyve 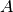 arba nuliui, jei tokio elemento
masyve nėra. Žinoma, priklausomai nuo masyvo rėžių gali tekti
kitaip pažymėti nesėkmingą paieškos baigtį.
arba nuliui, jei tokio elemento
masyve nėra. Žinoma, priklausomai nuo masyvo rėžių gali tekti
kitaip pažymėti nesėkmingą paieškos baigtį.
Tiesinės paieškos sudėtingumas, kaip teigia ir pats pavadinimas, yra
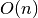 . Netgi žinant, kad ieškomasis elementas tikrai yra
masyve, vidutiniškai teks atlikti
. Netgi žinant, kad ieškomasis elementas tikrai yra
masyve, vidutiniškai teks atlikti 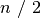 patikrinimų (jei bet
koks elementų išsidėstymas masyve vienodai tikėtinas). Taigi
atliekamų veiksmų skaičius tiesiškai priklauso nuo masyvo ilgio
patikrinimų (jei bet
koks elementų išsidėstymas masyve vienodai tikėtinas). Taigi
atliekamų veiksmų skaičius tiesiškai priklauso nuo masyvo ilgio
 .
.
Svarbiausias šio algoritmo privalumas – paprastumas.
Dvejetainė paieška¶
Daug efektyviau galima atlikti paiešką išrikiuotame masyve – prisiminkime, kaip greitai randame norimą telefono numerį storoje telefonų knygoje.
Dvejetainės paieškos (angl. Binary search) principas labai paprastas: ieškomasis elementas palyginamas su surikiuotos sekos viduriniu nariu. Jei jie yra lygūs, vadinasi, radome ieškomą elementą sekoje. Jei ieškomasis elementas yra mažesnis už vidurinį, tai juo labiau jis mažesnis ir už visus „dešiniuosius“ sekos narius, todėl paiešką tęsime kairiojoje sekos dalyje. Analogiškai, jei ieškomasis elementas didesnis už vidurinį, paiešką tęsime dešiniojoje masyvo dalyje. Toliau ieškoma tuo pačiu principu, kol randamas ieškomas elementas arba paieškos sritis tampa tuščia.
Aprašytąjį algoritmą nesudėtinga užrašyti rekursyvia funkcija. Nesėkmingos paieškos atveju ši funkcija grąžins nulį, o sėkmingos – ieškomo elemento indeksą masyve.
function ieškok(x, k, d : integer;
var A : masyvas) : integer;
var v : integer;
begin
if k > d then
ieškok := 0
else begin
v := (k + d) div 2;
{ pagal vidurinį masyvo dalies elementą toliau ieškoma
kairiojoje arba dešiniojoje masyvo dalyje }
if A[v] > x then
ieškok := ieškok(x, k, v - 1, A)
else if A[v] < x then
ieškok := ieškok(x, v + 1, d, A)
else { trečiuoju atveju A[v] = x (elementas rastas) }
ieškok := v;
end;
end;
int binSearch(int x, vector<int> arr) {
int lo = 0, hi = masyvas.size()-1;
// ieskome intervale [0, n-1]
while (lo < hi) {
int mid = (lo+hi)/2;
if (arr[mid] < x) {
lo = mid+1;
} else {
hi = mid;
}
}
return mid;
}
Taigi jei norime sužinoti, ar skaičius 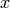 yra
yra  elementų masyve
elementų masyve 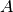 , turime patikrinti sąlygą
, turime patikrinti sąlygą
ieškok(A, x, 1, n) > 0.
Dvejetainės paieškos algoritmas kiekvienu žingsniu sutrumpina
paieškos sritį maždaug dvigubai. Kitaip tariant, jei masyvo ilgis
padidėja dvigubai, tai algoritmui tenka atlikti tik vieną papildomą
žingsnį. Dvejetainės paieškos sudėtingumas yra 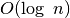 ,
t. y. logaritminis. Milijardo elementų dydžio masyve paieškai
prireiktų ne daugiau kaip 30 žingsnių. Tačiau sąlygą, kad masyvas
turi būti išrikiuotas, ne visuomet paprasta patenkinti.
,
t. y. logaritminis. Milijardo elementų dydžio masyve paieškai
prireiktų ne daugiau kaip 30 žingsnių. Tačiau sąlygą, kad masyvas
turi būti išrikiuotas, ne visuomet paprasta patenkinti.
Dvejetainės paieškos idėją galima panaudoti ne tik elemento
paieškai išrikiuotame masyve. Geras pavyzdys – žaidimas Atspėk
skaičių: pirmasis žaidėjas sugalvoja skaičių nuo 1 iki  ,
o antrasis bando jį atspėti; po kiekvieno spėjimo pirmasis žaidėjas
pasako, ar jo sugalvotasis skaičius yra mažesnis, didesnis ar lygus
spėtajam; žaidimo tikslas – atspėti skaičių kuo mažesniu
bandymų skaičiumi. Vėliau žaidėjai apsikeičia vaidmenimis. Iš
tiesų dvejetainė paieška – optimali spėjimo strategija. Nepaisant
to, gali laimėti žaidėjas, kuriam tądien labiau sekasi.
,
o antrasis bando jį atspėti; po kiekvieno spėjimo pirmasis žaidėjas
pasako, ar jo sugalvotasis skaičius yra mažesnis, didesnis ar lygus
spėtajam; žaidimo tikslas – atspėti skaičių kuo mažesniu
bandymų skaičiumi. Vėliau žaidėjai apsikeičia vaidmenimis. Iš
tiesų dvejetainė paieška – optimali spėjimo strategija. Nepaisant
to, gali laimėti žaidėjas, kuriam tądien labiau sekasi.
Bendriausiu atveju dvejetainę paiešką galima pritaikyti sprendžiant
lygtį 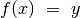 tam tikrame intervale, kur
tam tikrame intervale, kur
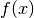 – monotoninė (nedidėjanti
arba nemažėjanti) funkcija.
– monotoninė (nedidėjanti
arba nemažėjanti) funkcija.
Kada rikiuoti?¶
Jei programoje laikome masyvą, kuriame teks ieškoti elementų, reikia atsakyti į klausimą: ar nerikiuoti masyvo ir atlikti tiesinę paiešką, ar išrikiuoti masyvą ir ieškoti jame naudojant daug efektyvesnę dvejetainę paiešką.
Olimpiadose programos paprastumas – didelė vertybė. Todėl visuomet geriau naudoti kuo paprastesnius algoritmus, jei tik programos veikimo laikas yra pakankamas.
Tarkime, masyvą sudaro  elementų, o jame žadame ieškoti
elementų, o jame žadame ieškoti
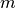 kartų. Naudodami tiesinę paiešką nerikiuotame masyve,
užtruksime
kartų. Naudodami tiesinę paiešką nerikiuotame masyve,
užtruksime 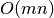 laiko. Masyvo rikiavimas ir
laiko. Masyvo rikiavimas ir 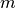 kartų
atlikta dvejetainė paieška užtruktų
kartų
atlikta dvejetainė paieška užtruktų
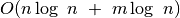 . Taigi, šiuo atveju rikiuoti masyvą
verta tik tada, kai
. Taigi, šiuo atveju rikiuoti masyvą
verta tik tada, kai 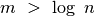 .
.
Rikiavimo uždaviniai olimpiadose, uždavinys Sekos rikiavimas¶
Olimpiadose tiesioginių rikiavimo ar paieškos uždavinių pasitaiko retai. Daug dažniau rikiavimas ir paieška tėra kito, sudėtingesnio, algoritmo dalis 1.
Tuo tarpu uždaviniams, kuriuose tiesiogiai minimas rikiavimas, dažniausiai reikia sugalvoti kokią nors kitą originalią idėją, o ne taikyti žinomus rikiavimo ar paieškos algoritmus.
Kaip pavyzdį panagrinėkime pasaulinės informatikų olimpiados uždavinį Sekos rikiavimas 2.
Duota skaičių seka, kurios nariai gali įgyti tik tris skirtingas reikšmes: vienetą, dvejetą ir trejetą. Seką reikia surikiuoti nemažėjimo tvarka. Rikiuojama sukeičiant vietomis po du sekos narius.
Užduotis. Reikia rasti minimalų sukeitimo operacijų, reikalingų sekai surikiuoti, skaičių.
Toliau pateikti piešiniai iliustruoja rikiavimo algoritmą rikiuojantį seką minimaliu sukeitimų skaičiumi.
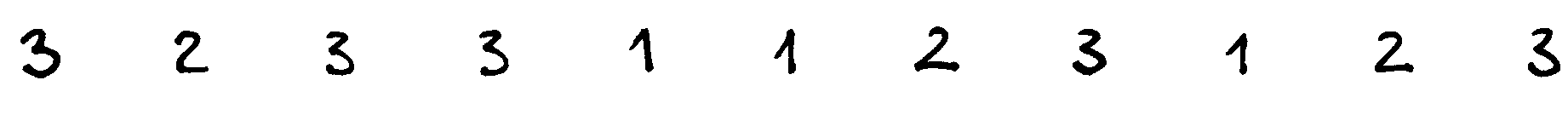
Fig. 24 Uždavinio „Sekos rikiavimas“ sprendimo iliustracija; paveiksle pateikta seka, kurią reikia išrikiuoti¶
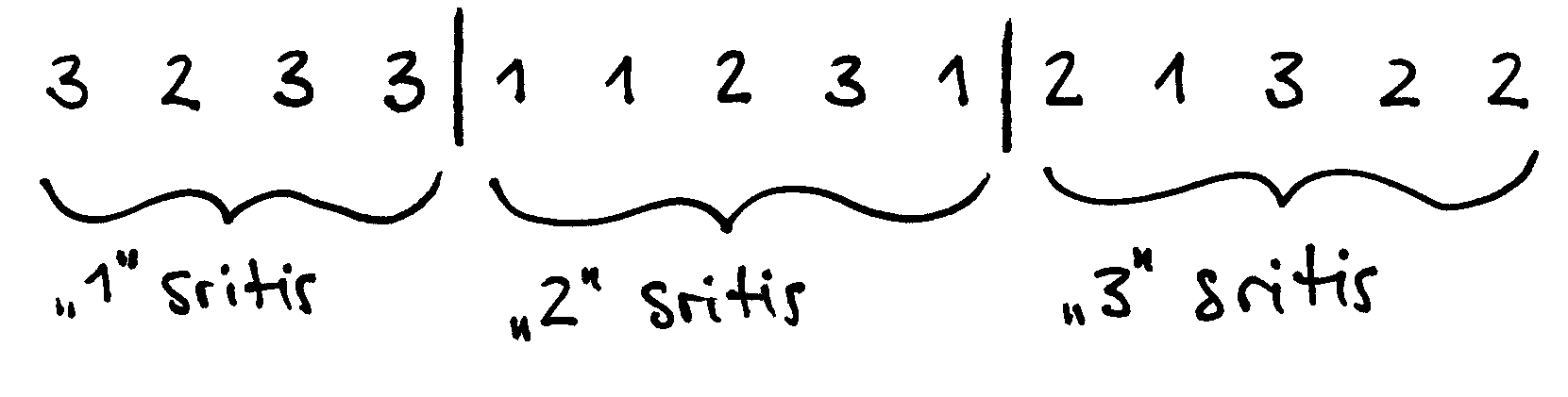
Fig. 25 1 žingsnis: suskaičiuojama, kiek sekoje yra vienetų, dvejetų ir trejetų (šiuo atveju 4 vienetai, 5 dvejetai ir 5 trejetai), ir seka padalijama į vienetų, dvejetų ir trejetų sritis¶
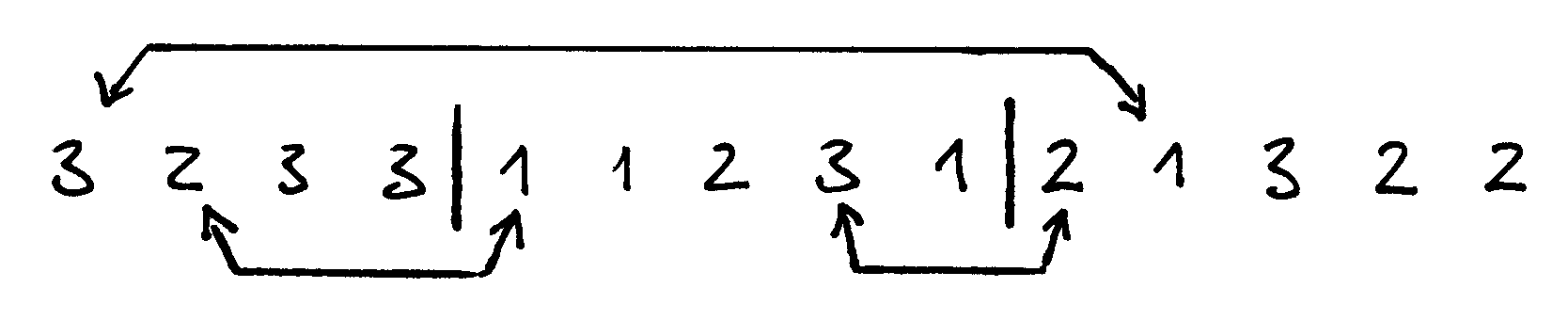
Fig. 26 2 žingsnis: randamos visos poros, kurių narius sukeitus vietomis, abu atsidurs savo srityse, ir atliekami sukeitimai¶
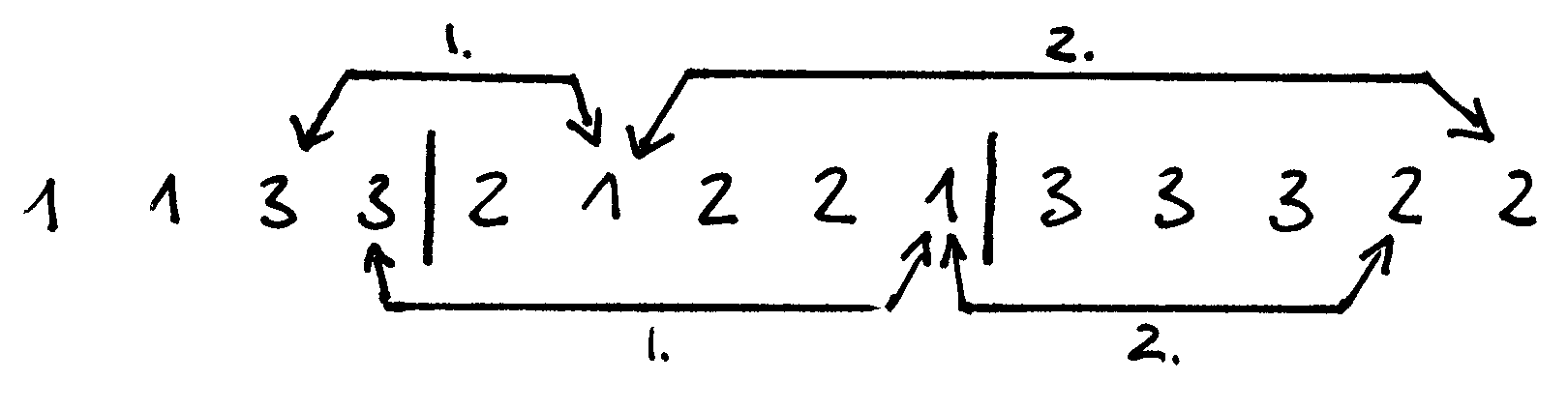
Fig. 27 3 žingsnis: ne savo srityse likę skaičiai sukeitinėjami po tris; kiekvienam trejetui sutvarkyti prireiks dviejų sukeitimų¶
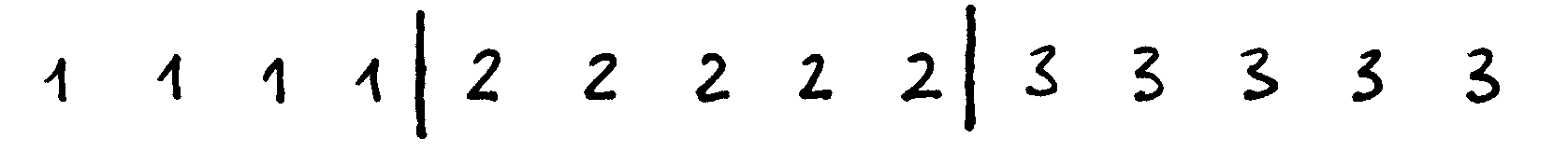
Fig. 28 Gavome surikiuotą seką: buvo atlikti 7 sukeitimai, sukeitimų skaičius yra minimalus¶
Išnašos
- 1
Programavimo kalbų C ir C++ standartinėse bibliotekose yra realizuoti svarbiausi paieškos ir rikiavimo algoritmai, tad juos galima taikyti neprogramuojant šių algoritmų.
- 2
Šis uždavinys buvo pateiktas 1996 metais Vengrijoje vykusioje Pasaulinėje informatikos olimpiadoje. Čia pateikėme sutrumpintą sąlygą.