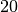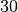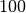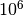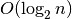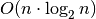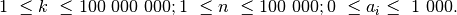Intuityvios algoritmo bei algoritmo sudėtingumo sąvokos¶
Algoritmas¶
Languages come and go, but algorithms stand the test of time.Programavimo kalbos atsiranda ir išnyksta, bet algoritmai išlieka ilgam.Donaldas Knutas (Donald Knuth)
Algoritmo sąvoka atsirado daugiau kaip prieš tūkstantį metų, o pats žodis kilo iš IX a. persų matematiko Mohamedo ibn Musos al Chorezmio (Al-Khwarizmi) vardo. Algoritmu sutarta vadinti seką elementarių veiksmų, pradinius duomenis paverčiančių rezultatais. Algoritmas yra teisingas, jei su visais pradiniais duomenimis baigia darbą ir gaunami teisingi rezultatai.
Koks algoritmas yra geras? Į šį klausimą puikiai atsakyta jau klasika tapusioje knygoje „Įvadas į algoritmus“ [CLR90]:
Geras algoritmas – kaip aštrus peilis – atlieka tiksliai tai, ką turi atlikti, su minimaliomis pastangomis. Netinkamo algoritmo naudojimas problemai spręsti primena bandymą perpjauti kepsnį atsuktuvu: anksčiau ar vėliau gali pavykti pasiekti patenkinamą rezultatą, tačiau teks išnaudoti daug daugiau pastangų negu būtina, ir pats rezultatas nekels estetinio pasigėrėjimo.
Geras algoritmas turi būti teisingas ir efektyvus laiko ir atminties požiūriu. Jis taip pat turi būti lengvai realizuojamas, t. y. užrašomas realia programavimo kalba. Dažniausiai visų tikslų pasiekti nepavyksta ir tenka nusileisti iki kompromiso. Mokslininkai teoretikai linkę skirti dėmesį teisingumui ir efektyvumui, nes jie retai patys programuoja savo algoritmus. Tuo tarpu industrija renkasi vadinamąjį greitą ir purviną (angl. Quick and Dirty) darbo principą: bet kokia programa, kuri pateikia priimtinus rezultatus ir pernelyg nesulėtina darbo, yra tinkama, nepaisant to, kad gali būti ir geresnis algoritmas.
Atskirai paminėsime euristinius algoritmus. Ne visiems uždaviniams spręsti sugalvoti efektyvūs algoritmai, o teisingi, bet neefektyvūs algoritmai praktiškai nepritaikomi, nes jų vykdymas užtruktų per ilgai, pavyzdžiui, kelis šimtmečius. Jei uždavinį vis dėlto reikia spręsti, galvojami spartūs algoritmai, kurie nebūtinai suranda tikslų sprendinį, tačiau rastasis sprendinys dažniausiai yra artimas ieškomajam. Tokie optimizmu grįsti algoritmai vadinami euristiniais algoritmais arba tiesiog euristikomis.
Iš tiesų skyrelio pradžioje pateiktas algoritmo apibrėžimas tėra intuityvi ir matematiškai netiksli algoritmo sąvoka 1. Tačiau mums jos pakaks.
Algoritmo sudėtingumas¶
Kaip jau minėjome, yra uždavinių, kurių kompiuteris negali išspręsti per priimtiną laiką, ir būtų neišmintinga viltis, kad kompiuteriai gali greitai atlikti bet kokius skaičiavimus. Todėl svarbu mokėti įvertinti algoritmo sudėtingumą, t. y. nustatyti, kiek laiko ir atminties išteklių prireiks algoritmo vykdymui.
Kas gi yra spartus algoritmas? Kuo didesnis pradinių duomenų kiekis (arba dydis), tuo ilgiau veikia programos, apdorojančios šiuos duomenis. Taigi algoritmas yra spartus, jei ganėtinai greitai apdoroja didelius duomenų kiekius. Negalime sakyti, kad vienas rikiavimo algoritmas spartesnis už kitą, jei pirmasis 10 skaičių išrikiavo greičiau nei antrasis. Kas kita, jei tenka rikiuoti labai daug skaičių. Apskritai konkretūs laiko įverčiai dažniausiai neteikia naudos, kadangi priklauso nuo daugybės veiksnių – techninių kompiuterio parametrų, algoritmo realizacijos, kompiliatoriaus nustatymų ir pan.
Daug svarbiau žinoti, kaip algoritmo vykdymui reikalingi laiko ir atminties ištekliai priklauso nuo pradinių duomenų kiekio. Žinodami, kad rikiavimo algoritmo atliekamų veiksmų skaičius didėja proporcingai rikiuojamos sekos ilgio kvadratui, galėsime nuspręsti, ar toks efektyvumas priimtinas.
Algoritmo sudėtingumas laiko atžvilgiu vertinamas funkcija, apibrėžiančia atliekamų veiksmų skaičiaus priklausomybę nuo pradinių duomenų dydžio. Algoritmo sudėtingumas atminties atžvilgiu vertinamas funkcija, apibrėžiančia reikalingos atminties kiekio priklausomybę nuo pradinių duomenų dydžio.
Kas yra pradinių duomenų dydis? Tai priklauso nuo paties algoritmo. Pavyzdžiui, dažnam rikiavimo algoritmui duomenų dydį apibrėžia rikiuojamų skaičių kiekis, bet ne patys skaičiai. Tačiau yra rikiavimo algoritmų, kurių efektyvumas priklauso ir nuo pačių rikiuojamų skaičių, todėl šiuo atveju duomenų dydis papildomas ir maksimalia rikiuojamų skaičių reikšme.
Kaip įvertinti algoritmo sudėtingumą¶
Natūralus būdas įvertinti algoritmo sudėtingumą – apskaičiuoti, kiek
elementarių veiksmų (aritmetinių operacijų, kreipimųsi į atmintį)
jis atlieka. Susitarsime, kad visi elementarūs veiksmai įvykdomi
vienodai greitai 2. Žinodami, kiek vidutiniškai elementarių
veiksmų per sekundę atlieka kompiuteris, galėsime įvertinti vykdymui
reikalingą laiką. Panagrinėkime programos fragmentą, randantį
kvadratinėje 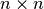 lentelėje surašytų skaičių sumą,
ir suskaičiuokime atliekamų elementarių veiksmų skaičių.
lentelėje surašytų skaičių sumą,
ir suskaičiuokime atliekamų elementarių veiksmų skaičių.
suma := 0; // atliekamas vieną kartą
read(n); // vieną kartą
for i := 1 to n do // n kartų
for j := 1 to n do begin // n*n kartų
read(a); // n*n kartų
suma := suma + a; // n*n kartų
// (priskyrimas ir sumavimas)
end;
writeln(suma); // vieną kartą
int suma = 0; // atliekamas vieną kartą
cin >> n; // vieną kartą
for(int i = 1; i <= n; i++) { // n kartų
for(int j = 1; j <= n; j++) { // n^2 kartų
cin >> a; // n^2 kartų
suma += a; // n^2 kartų
}
}
cout << suma << endl; // vieną kartą
Elementarių veiksmų skaičius lygus
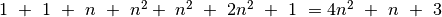 .
Jį nusako funkcija
.
Jį nusako funkcija 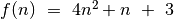 . Tai ir yra šio
fragmento sudėtingumas laiko atžvilgiu.
. Tai ir yra šio
fragmento sudėtingumas laiko atžvilgiu.
Jei paimtumėte kurią nors savo programą ir pabandytumėte pakartoti šiuos žingsnius, tikriausiai susiimtumėte už galvos! Kaip skaičiuoti, jei programoje yra ciklas while ar naudojama rekursija, jei priklausomai nuo įvairių sąlygų vieną kartą atliekami vieni, o kitą – kiti veiksmai.
Panagrinėkime kurį nors rikiavimo algoritmą. Jei pradiniai duomenys sudaro surikiuotą seką, tikriausiai bus atliekama mažiau veiksmų, negu rikiuojant atsitiktinę seką. Tad atliekamų elementarių veiksmų skaičius gali priklausyti ne tik nuo pradinių duomenų kiekio, bet ir nuo pačių duomenų.
Dėl šių priežasčių dažnai skaičiuojama, kiek veiksmų bus atliekama blogiausiu atveju, t. y. kiek daugiausiai elementarių veiksmų gali tekti atlikti vykdant algoritmą.
Kiekvienos programos veikimą nusakys vis kitokia funkcija. Tiksliai
suskaičiuoti elementarių veiksmų kiekį didesnėms programoms būtų
sudėtinga. Laimei, to daryti neteks! Panagrinėkime, kaip didėjant
 auga kiekvienas iš dėmenų. Kai
auga kiekvienas iš dėmenų. Kai 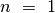 , dėmenys
lygūs
, dėmenys
lygūs 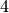 ,
, 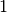 ir
ir 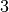 , kai
, kai 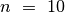 , jie
atitinkamai lygūs
, jie
atitinkamai lygūs 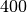 ,
, 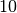 ir
ir 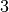 , kai
, kai
 , gauname
, gauname 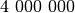 ,
,  ir
ir
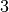 . Matome, kad didėjant
. Matome, kad didėjant  labiausiai didėja tik
pirmasis dėmuo, o kiti dėmenys – labai nežymiai. Kadangi kiekvienas
dėmuo tiesiogiai reiškia elementarių veiksmų skaičių, du
mažesniuosius dėmenis galime atmesti. Laikas, sugaištas atlikti
labiausiai didėja tik
pirmasis dėmuo, o kiti dėmenys – labai nežymiai. Kadangi kiekvienas
dėmuo tiesiogiai reiškia elementarių veiksmų skaičių, du
mažesniuosius dėmenis galime atmesti. Laikas, sugaištas atlikti
 veiksmams, yra nereikšmingas palyginti su laiku,
reikalingu atlikti keturiems milijonams veiksmų.
veiksmams, yra nereikšmingas palyginti su laiku,
reikalingu atlikti keturiems milijonams veiksmų.
Taigi, augant pradiniams duomenims 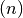 , algoritmo atliekamų
elementarių veiksmų skaičius vis labiau priklausys nuo greičiausiai
augančio funkcijos dėmens, t.y. nuo
, algoritmo atliekamų
elementarių veiksmų skaičius vis labiau priklausys nuo greičiausiai
augančio funkcijos dėmens, t.y. nuo 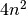 . Natūralu vietoj
funkcijos
. Natūralu vietoj
funkcijos 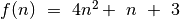 toliau nagrinėti
paprastesnę funkciją
toliau nagrinėti
paprastesnę funkciją 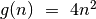 .
.
Tai dar ne viskas. Padidinus  dešimt kartų, vykdymo laikas
padidės šimtąkart. Palyginus su tuo, vykdymo laiko padidėjimas
keturis kartus yra neesminis. Taigi galime atmesti konstantą prie
dešimt kartų, vykdymo laikas
padidės šimtąkart. Palyginus su tuo, vykdymo laiko padidėjimas
keturis kartus yra neesminis. Taigi galime atmesti konstantą prie
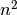 ir tarti, kad elementarių veiksmų skaičių pakankamai
gerai nusako dar paprastesnė funkcija
ir tarti, kad elementarių veiksmų skaičių pakankamai
gerai nusako dar paprastesnė funkcija 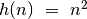 .
.
Mokslininkai rašytų, kad nagrinėto programos fragmento sudėtingumas yra
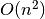 . Mat visur, kur kalbama apie algoritmų sudėtingumą,
naudojamas didžiosios O žymėjimas.
. Mat visur, kur kalbama apie algoritmų sudėtingumą,
naudojamas didžiosios O žymėjimas.
Didžiosios O žymėjimas¶
Formaliai algoritmo sudėtingumas apibrėžiamas taip:
Tarkime, pradinių duomenų dydis yra  , o algoritmo atliekamų
elementarių veiksmų skaičius –
, o algoritmo atliekamų
elementarių veiksmų skaičius – 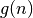 . Sakysime, jog algoritmo
sudėtingumas yra
. Sakysime, jog algoritmo
sudėtingumas yra 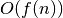 (rašome
(rašome 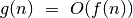 ),
jei egzistuoja tokie skaičiai
),
jei egzistuoja tokie skaičiai  ir
ir 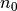 , su kuriais visiems
, su kuriais visiems
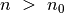 galioja nelygybės:
galioja nelygybės: 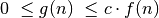 .
.
Geriau suprasti šį apibrėžimą padės Fig. 1
paveiksle pateikti funkcijų 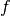 ir
ir 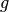 grafikai.
grafikai.

Fig. 1 Funkcijų grafikai: 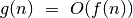 ¶
¶
Šis formalus apibrėžimas reiškia, kad, augant  , funkcija
, funkcija 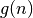 auga ne sparčiau nei funkcija
auga ne sparčiau nei funkcija 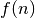 .
.
Sutartiniu didžiosios O žymėjimu paprastai parodoma, kaip elgsis algoritmas didėjant pradiniams duomenims, t. y. kaip augs algoritmui reikalingos atminties dydis arba vykdymo laikas.
Panagrinėkime dar keletą pavyzdžių:
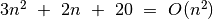 ,
, ,
,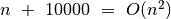 (pagal apibrėžimą teisingas teiginys,
tačiau parankesnė praeita lygybė),
(pagal apibrėžimą teisingas teiginys,
tačiau parankesnė praeita lygybė),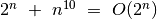 .
.
Jei algoritmo sudėtingumas nepriklauso nuo duomenų kiekio (t. y. jis
pastovus, konstantinis), tai jį žymėsime 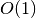 . Pavyzdžiui, atminties,
kurią naudoja nagrinėtas programos fragmentas, dydis lygus
. Pavyzdžiui, atminties,
kurią naudoja nagrinėtas programos fragmentas, dydis lygus 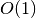 .
.
Pradinių duomenų dydį gali nusakyti ne vienas, o keli kintamieji. Tokiu
atveju didžiosios O žymėjimas aprašo sudėtingumo augimą didėjant visiems
parametrams. Pavyzdžiui, galimi tokie algoritmo sudėtingumo variantai:
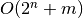 ,
, 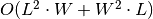 .
.
Nusakant algoritmų sudėtingumą dažnai teks susidurti su šiomis funkcijomis:
Kaip tai pritaikyti olimpiadoje¶
Olimpiadose ribojamas programų veikimo laikas ir naudojamoji atmintis. Taigi apmąstant įvairius sprendimo būdus reikia mokėti įvertinti, ar programa bus pakankamai efektyvi (ar suspės įveikti uždavinį su visais pradiniais duomenimis per leistiną laiką). Tačiau kiek gi veiksmų gali atlikti kompiuteris per, pavyzdžiui, vieną sekundę? Tai priklauso nuo daugelio dalykų: nuo procesoriaus, kompiliatoriaus, pačių veiksmų, kuriuos programa atlieka. Atliekamų veiksmų skaičių mums padės įvertinti paprasta programa:
uses windows;
var pradžia, veiksmųSk : longint;
begin
veiksmųSk := 0;
pradžia := GetTickCount;
while GetTickCount - pradžia < 1000 do
inc(veiksmųSk);
writeln(veiksmųSk);
end.
#include <chrono>
#include <iostream>
using namespace std;
// Gauna laiką, praėjusį nuo 1970 m. sausio 1 d. milisekundėmis
long long dabartinisLaikas() {
return chrono::duration_cast<chrono::milliseconds>(chrono::system_clock::now().time_since_epoch()).count();
}
int main() {
int veiksmųSk = 0;
long long pradžia = dabartinisLaikas();
while (dabartinisLaikas() - pradžia < 1000) {
veiksmųSk++;
}
cout << veiksmųSk << endl;
return 0;
}
Ši programa suskaičiuoja, kiek elementarių veiksmų kompiuteris gali atlikti per vieną sekundę (suprantama, jei programą pradėjote ir baigėte vykdyti tą pačią parą). Be abejo, matavimai nėra visiškai tikslūs, tačiau jų pakanka įvertinti kompiuterio spartai.
Taigi tarkime, kad duomenų dydis yra  ,
, 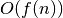 sudėtingumo
algoritmas atlieka lygiai
sudėtingumo
algoritmas atlieka lygiai 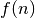 elementarių veiksmų, o atlikę
pateiktą programą įvertinome, kad kompiuteris per 1 sekundę atlieka
elementarių veiksmų, o atlikę
pateiktą programą įvertinome, kad kompiuteris per 1 sekundę atlieka
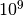 tokių veiksmų. Sudarykime lentelę, atspindinčią, kiek laiko
trunka įvairaus sudėtingumo algoritmų vykdymas su įvairiais pradiniais
duomenimis.
tokių veiksmų. Sudarykime lentelę, atspindinčią, kiek laiko
trunka įvairaus sudėtingumo algoritmų vykdymas su įvairiais pradiniais
duomenimis.
|
|
|
|
|
|
|
|
|
~0 |
~0 |
~0 |
~0 |
~0 |
~0 |
~0 |
|
~0 |
~0 |
~0 |
~0 |
~0 |
~0 |
~0 |
|
~0 |
~0 |
~0 |
~0 |
~0 |
~0 |
~0,03 ms |
|
~0 |
~0 |
~0 |
~0 |
~0 |
~1 ms |
~1 s |
|
~0 |
~0 |
~0 |
~0 |
~0 |
~20 ms |
~30 s |
|
~0 |
~0 |
~0 |
~0 |
~1 ms |
~17 min |
~32 metai |
|
~0 |
~0 |
~0.03 ms |
~1 ms |
~1 s |
~32 metai |
~32 * 109 metų |
|
~0 |
~1 ms |
~1 s |
~4 * 1013 metų |
– |
– |
– |
|
~4 ms |
~77 metai |
~8 * 1015 metų |
– |
– |
– |
– |
Sunku patikėti, bet tai tiesa: naivus skaičių rikiavimo algoritmas,
kuris bando visus įmanomus skaičių išdėstymo būdus (tokių yra 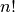 ), ir
tikrina, ar gautoji skaičių seka yra didėjanti, dvidešimt skaičių
„rikiuotų“ daug metų. Toks algoritmas, žinoma, yra neefektyvus.
), ir
tikrina, ar gautoji skaičių seka yra didėjanti, dvidešimt skaičių
„rikiuotų“ daug metų. Toks algoritmas, žinoma, yra neefektyvus.
Efektyviais laikomi polinominio sudėtingumo algoritmai, t. y. tokie,
kurių sudėtingumo funkcija yra polinomas – 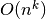 . Pirmieji
septyni lentelėje pateikti sudėtingumai yra polinominiai, taigi laikomi
efektyviais. Algoritmai, kurių sudėtingumas nepolinominis, laikomi
neefektyviais. Tokie yra eksponentinio (pavyzdžiui,
. Pirmieji
septyni lentelėje pateikti sudėtingumai yra polinominiai, taigi laikomi
efektyviais. Algoritmai, kurių sudėtingumas nepolinominis, laikomi
neefektyviais. Tokie yra eksponentinio (pavyzdžiui, 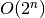 ) ir
faktorialinio (
) ir
faktorialinio (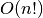 ) sudėtingumo algoritmai.
) sudėtingumo algoritmai.
Šią lentelę verta įsidėmėti. Olimpiados metu, sugalvoję uždavinio sprendimą, galime įvertinti jo sudėtingumą ir patikrinti, ar to užteks pradiniams duomenims įveikti per leistiną laiką. Įgijus patirties, algoritmo sudėtingumą dažnai nesunku įvertinti pažvelgus į algoritmo struktūrą: kokie jame yra ciklai, kokie rekursiniai kreipiniai ir pan.
Dar daugiau: matydami, jog uždavinio pradiniai duomenys labai maži, žinome, kad pakaks ir neefektyvaus algoritmo uždaviniui spręsti. Ir atvirkščiai: jei uždavinio pradiniai duomenys yra dideli, o leistinas programos veikimo laikas – mažas, reikia ieškoti efektyvaus būdo, kaip spręsti šį uždavinį.
Beje, beveik visose programose 90% laiko sugaištama vykdant 10% kodo. Ir likusių 90% kodo optimizavimas, deja, neturės didelės įtakos programos efektyvumui. Tad prieš imantis optimizuoti kurią nors algoritmo dalį reikia įsitikinti, ar verta tai daryti.
Uždavinys Posekio suma¶
Pabandykime pritaikyti įgytas žinias spręsdami konkretų uždavinį:
Duotas sveikasis skaičius
bei
neneigiamų skaičių seka
.
Užduotis. Reikia nustatyti, ar egzistuoja tokie indeksai
ir
(
), kad sekos narių nuo
iki
suma būtų lygi skaičiui
.
Galioja ribojimai:
Vykdymo laikas: 1 s.
Aptarkime kelis galimus uždavinio sprendimo būdus bei jų sudėtingumą.
Pats paprasčiausias būdas – perrinkti visas galimas indeksų 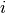 ir
ir
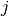 poras, kiekvienąkart suskaičiuojant sekos narių nuo
poras, kiekvienąkart suskaičiuojant sekos narių nuo
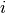 -ojo iki
-ojo iki 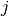 -ojo sumą:
-ojo sumą:
rasta := false;
i := 0;
repeat
j := i;
i := i + 1;
repeat
j := j + 1;
suma := 0;
for l := i to j do
suma := suma + a[l]; { ši operacija vykdoma daugiausiai kartų }
rasta := (suma = k);
until (j = n) or rasta;
until (i = n) or rasta;
C++ kodas atitinkantis Pascal:
bool rasta = false;
int i = -1;
do {
int j = i;
i++;
do {
j++;
int suma = 0;
for (int l = i; l <= j; l++) {
suma += a.at(l);
}
rasta = (suma == k);
} while (j < n-1 && !rasta);
} while (i < n-1 && !rasta);
Labiau idiomatinis C++ kodas:
bool rasta = false;
int atsPr, atsPab;
for(int i = 0; i < n && !rasta; i++) {
for(int j = i; j < n && !rasta; j++) {
int suma = 0;
for(int k = i; k <= j; k++) {
suma += a.at(k);
}
if (suma == K) {
atsPr = i;
atsPab = j;
rasta = true;
}
}
}
Jei algoritmui baigus darbą kintamojo rasta reikšmė bus lygi true, tai
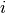 ir
ir 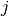 bus ieškomi indeksai. Suskaičiavę, kiek elementarių
veiksmų blogiausiu atveju atlieka algoritmas, pamatytume, kad greičiausiai
augantis gautojo reiškinio dėmuo yra
bus ieškomi indeksai. Suskaičiavę, kiek elementarių
veiksmų blogiausiu atveju atlieka algoritmas, pamatytume, kad greičiausiai
augantis gautojo reiškinio dėmuo yra 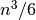 , taigi šio
algoritmo sudėtingumas –
, taigi šio
algoritmo sudėtingumas – 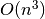 . Tai atsispindi ir algoritmo
struktūroje: jį sudaro trys ciklai, įdėti vienas į kitą, ir kiekvieno
šių ciklų trukmė tiesiogiai priklauso nuo
. Tai atsispindi ir algoritmo
struktūroje: jį sudaro trys ciklai, įdėti vienas į kitą, ir kiekvieno
šių ciklų trukmė tiesiogiai priklauso nuo  .
.
Tai nėra geriausias uždavinio sprendimo būdas. Pasižiūrėjus į 1.5
skyrelyje pateiktą lentelę 6, matyti, kad per leistiną laiką algoritmas
įveiktų testus, kur 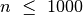 . Atkreipę dėmesį į tai, kad sekos nariai
yra tik neneigiami skaičiai, galime sudaryti gudresnį algoritmą.
. Atkreipę dėmesį į tai, kad sekos nariai
yra tik neneigiami skaičiai, galime sudaryti gudresnį algoritmą.
Tegul ieškomasis indeksas 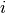 lygus
lygus 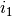 (t. y. kažkokiam
konkrečiam skaičiui). Priskyrę indeksui
(t. y. kažkokiam
konkrečiam skaičiui). Priskyrę indeksui 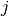 pradinę reikšmę
pradinę reikšmę
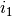 , jį didinsime tol, kol sekos narių nuo
, jį didinsime tol, kol sekos narių nuo 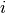 iki
iki 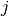 suma
taps lygi arba viršys
suma
taps lygi arba viršys  (arba kol indeksas
(arba kol indeksas 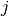 pasieks sekos
pabaigą). Sumos neperskaičiuosime iš naujo kiekvieną kartą, o, padidinę
indeksą
pasieks sekos
pabaigą). Sumos neperskaičiuosime iš naujo kiekvieną kartą, o, padidinę
indeksą 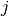 , prie sumos tiesiog pridėsime sekos narį
, prie sumos tiesiog pridėsime sekos narį 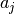 .
.
rasta := false;
i := 0;
repeat
j := i;
i := i + 1;
suma := 0;
repeat
j := j + 1;
suma := suma + a[j];
until (j = n) or (suma >= k);
rasta := (suma = k);
until (i = n) or rasta;
bool rasta = false;
int atsPr, atsPab;
for(int i = 0; i < n && !rasta; i++) {
int suma = 0;
for(int j = i; j < n && !rasta; j++) {
suma += a[j];
if (suma == K) {
atsPr = i;
atsPab = j;
rasta = true;
}
}
}
Šį algoritmą sudaro du ciklai, antrasis jų pirmojo viduje, ir abiejų
ilgis tiesiogiai priklauso nuo  . Blogiausiu atveju abiejuose cikluose
bus vykdoma
. Blogiausiu atveju abiejuose cikluose
bus vykdoma  žingsnių (pavyzdžiui, jei visi sekos nariai – nuliai,
tuomet suma niekada netaps lygi arba didesnė už
žingsnių (pavyzdžiui, jei visi sekos nariai – nuliai,
tuomet suma niekada netaps lygi arba didesnė už  ), taigi šio
algoritmo sudėtingumas yra
), taigi šio
algoritmo sudėtingumas yra 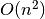 . Tai daug geresnis
algoritmas, jis gali įveikti testus, kur
. Tai daug geresnis
algoritmas, jis gali įveikti testus, kur 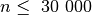 .
Tačiau to nepakanka.
.
Tačiau to nepakanka.
Kritiškai įvertinkime savo algoritmą. Tarkime, 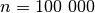 ,
,
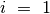 ,
, 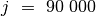 , ir suma
, ir suma 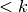 . Kas atsitiks, jei,
padidinus
. Kas atsitiks, jei,
padidinus 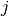 dar vienetu, suma taps didesnė už
dar vienetu, suma taps didesnė už  ?
Indeksas
?
Indeksas 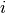 bus padidintas vienetu,
bus padidintas vienetu, 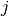 priskirta
priskirta 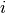 reikšmė ir iš naujo skaičiuojamos sumos. Tačiau jei sekos narių nuo
reikšmė ir iš naujo skaičiuojamos sumos. Tačiau jei sekos narių nuo 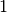 iki
iki 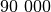 suma buvo mažesnė už
suma buvo mažesnė už  , tai tuo labiau tokia bus ir
narių nuo
, tai tuo labiau tokia bus ir
narių nuo 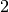 iki
iki 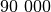 suma. Šio (milžiniško) intervalo būtų
galima netikrinti!
suma. Šio (milžiniško) intervalo būtų
galima netikrinti!
Tai apibendrinę, galime sudaryti dar geresnį algoritmą. Priskirkime
indeksams reikšmes 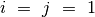 , o sumai reikšmę
, o sumai reikšmę 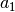 . Tai
bus pradinis intervalas. Veiksmus kartosime, kol suma nelygi
. Tai
bus pradinis intervalas. Veiksmus kartosime, kol suma nelygi  ir
ir
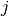 mažesnis už
mažesnis už  . Kiekvienu žingsniu vykdysime vieną iš šių
veiksmų: jei suma mažesnė už
. Kiekvienu žingsniu vykdysime vieną iš šių
veiksmų: jei suma mažesnė už  , intervalą praplėsime – padidinsime
indeksą
, intervalą praplėsime – padidinsime
indeksą 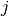 ir prie sumos pridėsime
ir prie sumos pridėsime 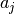 ; jei suma didesnė
už
; jei suma didesnė
už  (tai tokia ji tapo po paskutinio žingsnio), intervalą siaurinsime
– iš sumos atimsime
(tai tokia ji tapo po paskutinio žingsnio), intervalą siaurinsime
– iš sumos atimsime 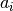 ir padidinsime indekso
ir padidinsime indekso 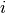 reikšmę.
Jei po kurio nors žingsnio suma taps lygi
reikšmę.
Jei po kurio nors žingsnio suma taps lygi  , algoritmas iškart
nutrauks darbą.
, algoritmas iškart
nutrauks darbą.
suma := a[1];
i := 1;
j := 1;
while (suma <> k) and (j < n) do
if suma < k then begin
j := j + 1;
suma := suma + a[j];
end else begin
suma := suma - a[i];
i := i + 1;
end;
rasta := (suma = k);
int suma = a[0];
int i = 0, j = 0;
while (suma != K && j < n) {
if (suma < K) {
j++;
if (j < n) {
suma += a[j];
}
}
else if (suma > K) {
suma -= a[i];
i++;
}
}
bool rasta = suma == K;
Kadangi vienu žingsniu padidinamas tik vienas iš indeksų ir kiekvienas
iš indeksų gali būti padidintas ne daugiau kaip  kartų, daugių
daugiausia gali tekti įvykdyti
kartų, daugių
daugiausia gali tekti įvykdyti 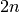 žingsnių. Algoritmo sudėtingumas
yra
žingsnių. Algoritmo sudėtingumas
yra 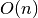 , taigi jo visiškai pakaks uždaviniui įveikti ir kai
, taigi jo visiškai pakaks uždaviniui įveikti ir kai
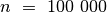 .
.
Aptarėme kelis uždavinio Posekio suma sprendimus ir skirtingą jų efektyvumą. Atsiminkime, jog geras algoritmas atlieka tik tai, kas būtina. Ieškodami, kaip galime pagerinti algoritmą, galvokime, kokius nereikalingus arba pakartotinius veiksmus jis atlieka.
NP sudėtingumas¶
Skaitydami knygas apie algoritmus ir uždavinių sprendimus, ne kartą sutiksite mistiškai skambančią frazę uždavinys yra NP pilnas.
Uždavinys priklauso NP (nondeterministic polynomial time) sudėtingumo klasei, jei, žinodami šio uždavinio sprendinį, per polinominį laiką galime patikrinti, ar sprendinys teisingas. NP uždavinį galima išspręsti perrinkimu per eksponentinį laiką generuojant visus galimus sprendinius, ir kiekvieną sprendinį patikrinant per polinominį laiką.
NP klasei priklauso daug labai gerai žinomų ir plačiai nagrinėtų kombinatorinių optimizavimo uždavinių. Vieni jų yra paprastesni (išsprendžiami per polinominį laiką), kitiems, sudėtingesniems, uždaviniams, žinomi tik perrenkantys visus sprendinius algoritmai.
NP pilnas uždavinys yra toks uždavinys, kuris yra ne lengvesnis už visus kitus NP uždavinius. Taigi frazę „uždavinys yra NP pilnas“ „išvertus“ į suprantamesnę kalbą, reikštų: niekam iki šiol nepavyko rasti efektyvaus uždavinį sprendžiančio algoritmo; tikėtina, kad toks algoritmas apskritai neegzistuoja.
Nepaisant sudėtingumo, šie uždaviniai gali turėti labai paprastą formuluotę, pavyzdžiui, tokią. Žinomi atstumai tarp N miestų; pirklys nori pradėti savo kelionę viename iš jų, apsilankyti kiekviename mieste tik po vieną kartą ir sugrįžti į pradinį miestą; užduotis – iš visų tokių maršrutų surasti trumpiausią.
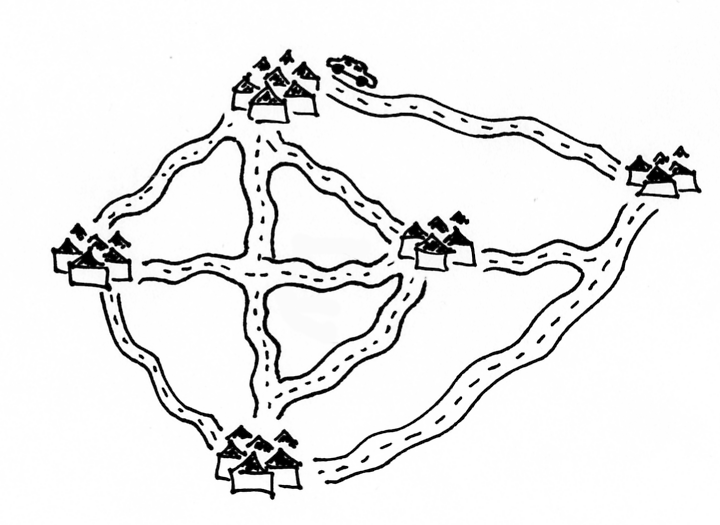
Fig. 2 Keliaujančio pirklio uždavinys¶
Šis uždavinys dar yra vadinamas Keliaujančio pirklio uždaviniu, o ieškomasis kelias – optimaliu Hamiltono ciklu.
Neįtikėtina, bet iki šiol niekas nesurado tikslaus ir efektyvaus
algoritmo, sprendžiančio šį uždavinį. Vienintelis žinomas būdas rasti
optimalų sprendinį bendru atveju – perrinkti visus įmanomus maršrutus
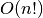 sudėtingumo (t.y. labai neefektyviu) algoritmu.
sudėtingumo (t.y. labai neefektyviu) algoritmu.
Ką gi daryti, jei olimpiadoje tenka spręsti uždavinį, kuris, jūsų žiniomis, yra NP pilnas? Tikrai neverta pulti į paniką. Svarbiausia, kad jūs tai jau žinote! Nereikia ieškoti tikslaus ir efektyvaus uždavinį sprendžiančio algoritmo manant, kad kiti jau tokį surado, o nesiseka tik jums. Verčiau skirkite savo laiką ir energiją kurti euristiniam algoritmui, kuris bendru atveju pateiktų kuo geresnius rezultatus (pavyzdžiui, kuo trumpesnius maršrutus), arba, jei pradiniai duomenys tikrai labai maži, – spręsti uždavinį perrinkimu.
Amžinybės dėlionė¶

Fig. 3 Amžinybės dėlionės daugiakampio pavyzdys¶
Kristoferis Montonas (Christopher Monton) sukūrė geometrinę dėlionę, kurią pavadino Amžinybės dėlione (angl. Eternity puzzle). Ji buvo sudaryta iš 209 įvairios formos netaisyklingų daugiakampių, iš kurių reikėjo sudėti dvylikakampį. Dauguma daugiakampių buvo skirtingi, o juos visaip sukiojant buvo galima pasiekti labai daug pozicijų (t.y. iš dalies daugiakampių sudėliotų geometrinių figūrų), kurios nenuvesdavo prie sprendinio.
K. Montonas užsakė pagaminti šią dėlionę, ir 1999 metų liepą ji atsidūrė parduotuvių lentynose. Jis taip pat pažadėjo, kad sumokės milijoną svarų tam, kuris pirmasis sudės šią dėlionę iki 2000 metų rugsėjo. Kilo visuotinis susidomėjimas dėlione, prekyba vyko labai sėkmingai: netgi Grenlandijoje buvo parduodami rekordiniai kiekiai dėlionių. Žmonės pirko, bandė sudėlioti dėlionę ir laimėti milijoną.
Prieš pažadėdamas milijoną, K. Montonas be abejo, konsultavosi su
matematikais, ir šie užtikrino, kad uždavinio neįmanoma išspręsti per
duotą laiką net ir su kompiuterio pagalba, nes tai NP pilnas uždavinys.
Vieni ekspertai spėjo, kad geriausiu atveju uždavinio sprendimas užtruks
apie ketverius metus. Kiti mokslininkai netgi teigė, kad uždavinio
sprendimas užtruks ilgiau nei gyvuos Visata. Nors visada lieka
atsitiktinio sudėliojimo tikimybė, buvo apskaičiuota, kad tikimybė vienu
bandymu atsitiktinai sudėlioti šią dėlionę yra 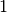 iš
iš 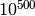 (palyginimui: tikimybė išlošti Didžiosios Britanijos nacionalinėje
loterijoje yra
(palyginimui: tikimybė išlošti Didžiosios Britanijos nacionalinėje
loterijoje yra 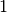 iš
iš 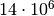 ).
).
K. Montonas buvo tikras, kad jo milijonas yra saugus. Už pinigus, gautus pardavus dėliones, jis tikėjosi suremontuoti jam priklausiusį 1825 metais pastatytą dvarą, turintį 67 kambarius ir 200 akrų žemės.
Tačiau du Kembridžo matematikai A. Serbis (Alex Serby) ir O. Riordanas (Oliver Riordan) sugebėjo sudėti dėlionę iki nurodytos datos. Jie pastebėjo, kad sudėlioti dėlionę iki tokios būsenos, kai likę daugiakampiai nebetelpa, yra gana paprasta. Tolesnė sėkmė priklauso nuo nepanaudotų daugiakampių rinkinio – kuo parankesnių formų jie yra ir kuo daugiau įvairios formos daugiakampių galima iš jų sudėti, tuo šis rinkinys parankesnis tolimesniems bandymams. Tokiu būdu jie atrinko „blogus“ gabalėlius ir optimizuotoje perrinkimo programoje stengėsi juos padėti pirmiausia. Ši strategija pasitvirtino ir keletas jų asmeninių kompiuterių per porą savaičių surado sprendinį. K. Montonui teko parduoti savo dvarą ir išmokėti milijoną…
Išnašos
- 1
Tikslios algoritmo sąvokos prireikė matematikams, panorusiems įrodyti, kad nėra algoritmo, sprendžiančio duotąjį uždavinį. 20-ajame amžiuje daug matematikų ieškojo būdo tiksliai apibrėžti algoritmo sąvoką. Galima sakyti, jog jiems pavyko. 1936 m. amerikiečių matematikas A. Čerčas (A. Church) paskelbė tezę, teigiančią, jog jo apibrėžta dalinių rekursyviųjų funkcijų (DRF) klasė sutampa su algoritmiškai apskaičiuojamų funkcijų klase. Tačiau tezės įrodyti negalima, kadangi neįmanoma palyginti matematiškai tikslios ir intuityviai suprantamos funkcijų klasių. Kita vertus, niekam nepavyko rasti algoritmo (intuityviąja prasme), kurio nebūtų galima realizuoti kaip DRF, o visos DRF apskaičiuojamos algoritmais intuityviąja prasme, todėl Čerčo tezė visuotinai laikoma teisinga.
- 2
Toks modelis kartais kritikuojamas, nes vieni elementarūs veiksmai įvykdomi greičiau negu kiti. Pavyzdžiui, skaičių perskaityti iš failo trunka ilgiau nei tą patį skaičių perskaityti iš operatyviosios atminties. Kelių knygų apie algoritmus autorius prof. S. Skienna drąsiai atremia tokią kritiką: Visi žinome, kad žemė yra apvali, tačiau statydami namą laikome ją plokščia ir toks modelis mums puikiausiai tinka. Tas pats galioja ir šiuo atveju. [S98]
- 3
Logaritmas yra funkcija, atvirkščia kėlimui laipsniu.
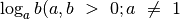 ;
;  vadinamas
logaritmo pagrindu) atsako į klausimą: kokiu laipsniu reikia pakelti
vadinamas
logaritmo pagrindu) atsako į klausimą: kokiu laipsniu reikia pakelti
 , kad gautume
, kad gautume 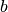 ? Pavyzdžiui,
? Pavyzdžiui, 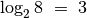 ,
,
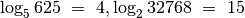 . Logaritmas – vienodai
lėtai auganti funkcija, nesvarbu koks logaritmo pagrindas. Taigi
logaritminis algoritmo sudėtingumas yra labai palankus.
Didžiosios O žymėjime logaritmo pagrindas dažnai nerašomas.
. Logaritmas – vienodai
lėtai auganti funkcija, nesvarbu koks logaritmo pagrindas. Taigi
logaritminis algoritmo sudėtingumas yra labai palankus.
Didžiosios O žymėjime logaritmo pagrindas dažnai nerašomas.- 4
Kvadratinė šaknis iš skaičiaus
 yra toks skaičius
yra toks skaičius  ,
kad
,
kad 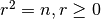 .
.- 5
Teigiamo skaičiaus
 faktorialu vadinama visų skaičių nuo 1 iki
faktorialu vadinama visų skaičių nuo 1 iki
 sandauga (
sandauga (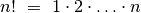 ).
).- 6
Turima omenyje, jog uždavinio sprendimą testuojančio kompiuterio spartą atitinka minėta lentelė.
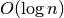 (logaritminis
(logaritminis 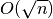 (šakninis
(šakninis 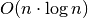 ,
,