Dinaminis programavimas¶
Computer science is no more about computersthan astronomy is about telescopes.Kompiuterių mokslą vadinti mokslu apie kompiuterius būtų tas pats,kas vadinti astronomiją mokslu apie teleskopus.Edsgeras V. Dijkstra (Edsger W. Dijkstra)
Apie dinaminį programavimą būtų galima pasakyti panašiai kaip ir apie kompiuterių mokslą: dinaminis programavimas neturi jokio tiesioginio ryšio su programavimu. Matematikai šį žodį vartoja nusakyti taisyklėms ir principams, kurių laikantis sprendžiamas uždavinys.
Dinaminis programavimas yra efektyvus sprendinių radimo būdas, kurį galima pritaikyti kai kuriems, ypač optimizavimo, uždaviniams spręsti.
Šį metodą pasiūlęs ir 1952 metais aprašęs amerikiečių mokslininkas Ričardas Belmanas savo autobiografijoje pasakoja, iš kur kilo pavadinimas Dinaminis programavimas:
1950-ieji metai buvo ne itin palankūs matematiniams tyrinėjimams. Tuo metu Vašingtone dirbo labai įdomus ponas, pavarde Vilsonas. Jis buvo gynybos sekretorius ir patologiškai bijojo to, kas vadinama moksliniais tyrinėjimais. <…> Jo veidas parausdavo ir jis įtūždavo, jei kas nors jam girdint pavartodavo šią sąvoką. Galite tik įsivaizduoti, kaip jį veikė žodis „matematika“. Tuomet aš dirbau RAND korporacijoje, kurią samdė Oro pajėgos, o pastarosios buvo pavaldžios ir Vilsonui. Taigi kažkokiu būdu reikėjo nuslėpti, kad užsiimu matematiniais tyrinėjimais. Kokį pavadinimą galėjau pasirinkti? Mane domino planavimas ir sprendimų priėmimas, tačiau „planavimas“ nebuvo tinkamas žodis, tad pasirinkau „programavimą“. Žodis „dinaminis“ atspindėjo daugiapakopiškumą, buvo būdvardis ir turėjo labai tikslią reikšmę fizikine prasme. <…> Kita vertus, šis žodis jokiame kontekste neįgaudavo menkinančios reikšmės. Tad pasirinkau pavadinimą, kuriam net Kongreso narys negalėjo prieštarauti ir tai buvo priedanga mano tolesniems darbams.
Uždavinių, sprendžiamų dinaminiu programavimu, dažnai pasitaiko olimpiadose. Šiame skyriuje apžvelgsime dinaminio programavimo principus. Iš pirmo žvilgsnio gali pasirodyti nelengva suprasti dinaminį programavimą, kadangi tai nėra algoritmas, o veikiau uždavinio sprendimo schema. Todėl daug dėmesio skirsime iliustravimui, kaip taikyti šį metodą sprendžiant konkrečius uždavinius.
Optimizavimo uždaviniai¶
Optimizavimo uždaviniu vadiname uždavinį, kai yra daug galimų sprendinių, kurių kiekvieną galima kaip nors įvertinti, o ieškoma sprendinio, turinčio tam tikrą (optimalią) vertę. Štai klasikinio optimizavimo uždavinio, vadinamo Kuprinės uždaviniu, pavyzdys:
Vagis, naktį įsilaužęs į muziejų, rado
vertingų eksponatų. Žinoma kiekvieno eksponato vertė
bei svoris
(sveikasis skaičius). Vagis gali panešti kuprinę, sveriančią ne daugiau kaip
kilogramų. Kuriuos eksponatus jis turėtų susikrauti į kuprinę, kad bendra jų vertė būtų kuo didesnė, o kuprinė – panešama?
Tai optimizavimo uždavinys, nes yra daug būdų sudaryti eksponatų rinkinį, kurį galėtų panešti vagis, ir kiekvienas jų turi tam tikrą vertę, o ieškoma rinkinio, kurio vertė maksimali.
Svarbu skirti sąvokas sprendinys ir sprendinio vertė. Mūsų pavyzdyje sprendinio vertė yra pasirinktų eksponatų verčių suma, o sprendinys yra pats eksponatų rinkinys. Optimizavimo uždaviniuose dažniausiai nesunku rasti bet kurį sprendinį (pavyzdžiui, bet kurį eksponatų rinkinį, kurį galėtų panešti vagis). Kur kas sunkiau rasti optimalų sprendinį (tokį panešamą eksponatų rinkinį, kurio vertė maksimali).
Optimizavimo uždavinių sprendimui galima taikyti godųjį algoritmą, kiekviename algoritmo žingsnyje pasirenkant geriausią variantą toje situacijoje (pavyzdžiui, rinktis eksponatus, kurių vertės ir svorio santykis kuo didesnis). Godieji algoritmai dažniausiai yra efektyvūs. Tačiau kiekviename žingsnyje renkantis lokalųjį optimumą, nebūtinai gaunamas globalusis optimumas. Reikia įsitikinti, kad godusis algoritmas tikrai ras geriausią sprendinį.
Minimalus jungiamasis medis skyriuje nagrinėta Minimalaus jungiamojo medžio paieška taip pat yra optimizavimo uždavinys, o jį sprendžiantys Primo bei Kruskalo algoritmai – godieji algoritmai.
Galima pamanyti, kad ir Kuprinės uždaviniui spręsti tiktų godusis
algoritmas: išrikiuoti eksponatus jų vertės ir svorio santykio
(t. y. svorio vieneto vertės) mažėjimo tvarka, ir paeiliui, kol
neviršijamas svoris  , rinkti kuo vertingesnius eksponatus iš
šio sąrašo. Deja, toks sprendimas ne visuomet randa optimalų
sprendinį. Pateiksime kontrpavyzdį. Tegu
, rinkti kuo vertingesnius eksponatus iš
šio sąrašo. Deja, toks sprendimas ne visuomet randa optimalų
sprendinį. Pateiksime kontrpavyzdį. Tegu 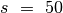 , o
eksponatų svoriai bei vertės pateikti lentelėje:
, o
eksponatų svoriai bei vertės pateikti lentelėje:
Nr. |
Svoris |
Vertė |
Svorio vieneto vertė |
1 |
10 |
60 |
6 |
2 |
20 |
100 |
5 |
3 |
30 |
120 |
4 |
Taikant godųjį algoritmą, būtų pasirenkami pirmasis ir antrasis eksponatai, kurių bendra vertė yra 160. Trečio eksponato nebepavyktų paimti, nes visi trys jie netilptų į kuprinę. Tuo tarpu pasirinkus antrąjį ir trečiąjį eksponatus, gaunama vertė 220.
Optimizavimo uždavinius galima spręsti perrinkimu: perrinkti visus įmanomus sprendinius ir iš jų išrinkti optimalų. Nors šiuo būdu galima rasti optimalų sprendinį, deja, perrinkimas praktiškai netaikomas, nes yra labai neefektyvus, t. y. nepolinominio sudėtingumo.
Dinaminis programavimas turi abiejų metodų gerąsias savybes: viena vertus, kiekviename žingsnyje pasirenkamas geriausias variantas (gaunamas efektyvus algoritmas), kita vertus – peržiūrimi visi galimi pasirinkimai, galintys vesti prie optimalaus sprendinio (randamas optimalus sprendinys).
Dinaminiu programavimu galima spręsti tuos optimizavimo uždavinius, kuriuose optimalų sprendinį pavyksta rekursyviai išreikšti per analogiškų, bet mažesnių optimizavimo uždavinių sprendinius.
Dinaminio programavimo principai¶
Uždavinio sprendimas dinaminiu programavimu susideda iš keturių žingsnių:
Nustatoma optimalaus sprendinio struktūra.
Rekursyviai apibrėžiama sprendinio vertė.
Apskaičiuojama optimalaus sprendinio vertė (skaičiuojant ją įsimenamos smulkesnių uždavinių sprendinių vertės, kurios panaudojamos ieškomai optimalaus sprendinio vertei rasti).
Sukonstruojamas pats optimalus sprendinys.
Jeigu reikia rasti ne patį optimalų sprendinį, o tik jo vertę, tuomet paskutinis žingsnis praleidžiamas.
Panagrinėsime labai paprastą uždavinį, sprendžiamą dinaminiu
programavimu ir kartu padėsiantį suvokti, kodėl dinaminiu
programavimu pagrįsti algoritmai yra efektyvūs. Prisiminkime
Fibonačį, triušius ir jo skaičius, apie kuriuos buvo rašyta
Rekursyvios funkcijos skyrelyje. Fibonačio skaičiai
apibrėžiami tokiu būdu: 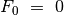 ,
, 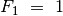 ,
,
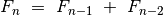 , reikia rasti
, reikia rasti  -ąjį
Fibonačio skaičių
-ąjį
Fibonačio skaičių  .
.
Tai nėra optimizavimo uždavinys. Sprendinio vertė jau apibrėžta rekursyviai, tereikia ją suskaičiuoti. Rekursyvios funkcijos skyrelyje buvo pateikta rekursinė funkcija, skaičiuojanti Fibonačio skaičius:
function F(n : longint) : longint;
begin
if n = 0 then
F := 0
else if n <= 2 then
F := 1
else
F(n - 1) + F(n - 2);
end;
long long F (long long n) {
if (n == 0)
return 0;
if (n <= 2)
return 1;
return F(n-1) + F(n-2);
}
Rekursyvios funkcijos skyrelyje rašėme, kad rekursyvus
Fibonačio skaičių skaičiavimas yra eksponentinio sudėtingumo (labai
lėtas). Pažvelkime į žemiau pateiktą kreipinio (į rekursinę
funkciją) F(6) skaičiavimų medį.
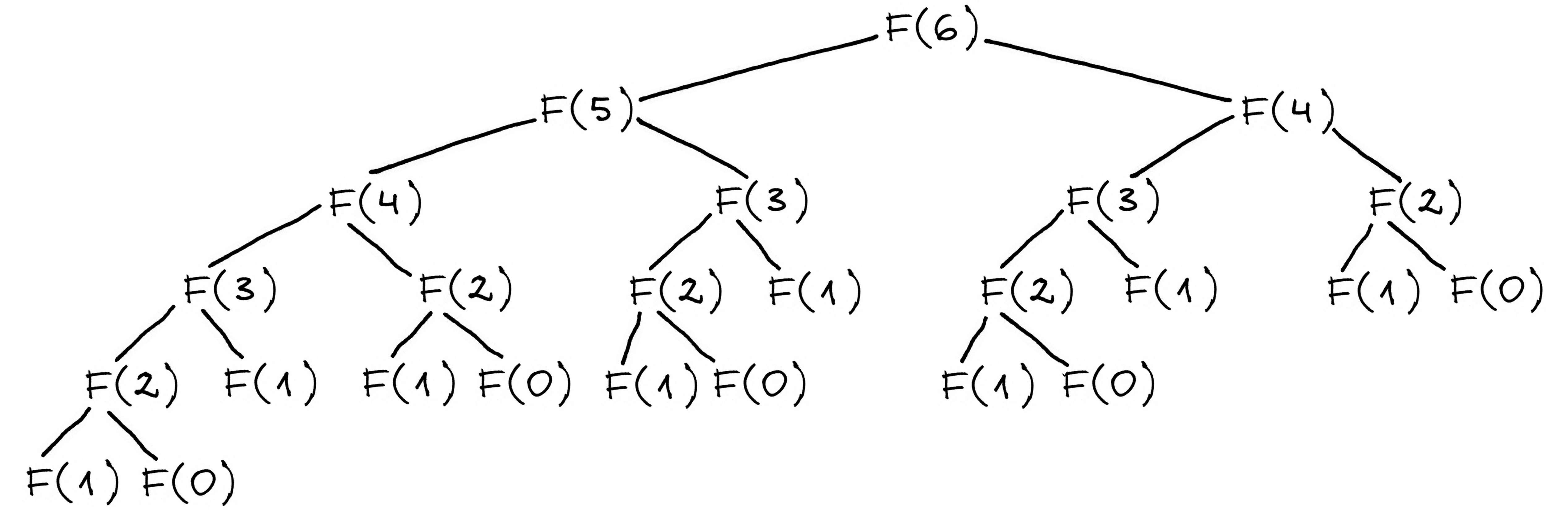
Fig. 71 Kreipinio F(6) į rekursinę funkciją skaičiavimų medis¶
Nesunku pastebėti, kad skaičiuojant 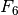 darbo atliekama kur
kas daugiau negu reikia. Tos pačios mažesnių Fibonačio skaičių
reikšmės perskaičiuojamos daug kartų. Pavyzdžiui, skaičiuojant
darbo atliekama kur
kas daugiau negu reikia. Tos pačios mažesnių Fibonačio skaičių
reikšmės perskaičiuojamos daug kartų. Pavyzdžiui, skaičiuojant
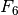 , net 5 kartus tenka skaičiuoti
, net 5 kartus tenka skaičiuoti 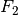 . Nesunku
įsivaizduoti, kaip atrodytų
. Nesunku
įsivaizduoti, kaip atrodytų 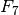 paieškos medis: reikėtų
atlikti beveik dvigubai daugiau darbo.
paieškos medis: reikėtų
atlikti beveik dvigubai daugiau darbo.
Taigi, būtų natūralu kartą suskaičiuotą reikšmę įsiminti masyve, ir jos daugiau neperskaičiuoti:
const MAX = ...;
var Fmas : array [0..MAX] of longint;
function F(n : longint) : longint;
begin
{ dar neapskaičiuotos reikšmės žymimos -1 }
if Fmas[n] <> -1 then
F := Fmas[n]
else if n = 0 then
F := 0
else if n = 1 then
F := 1
else begin
Fmas[n] := F(n - 1) + F(n - 2);
F := Fmas[n];
end;
end;
const int MAX = ...;
long long Fmas[MAX+1];
long long F (long long n) {
// dar neapsaičiuotos reikšmės žymimos -1
if (Fmas[n] != -1)
return Fmas[n];
if (n == 0)
return 0;
if (n <= 2)
return 1;
Fmas[n] = F(n-1) + F(n-2);
return Fmas[n];
}
Toliau pateiktas šios funkcijos rekursijos medis. Kvadratėliais įrėmintos reikšmės iš naujo nebeskaičiuojamos, o paimamos iš lentelės.
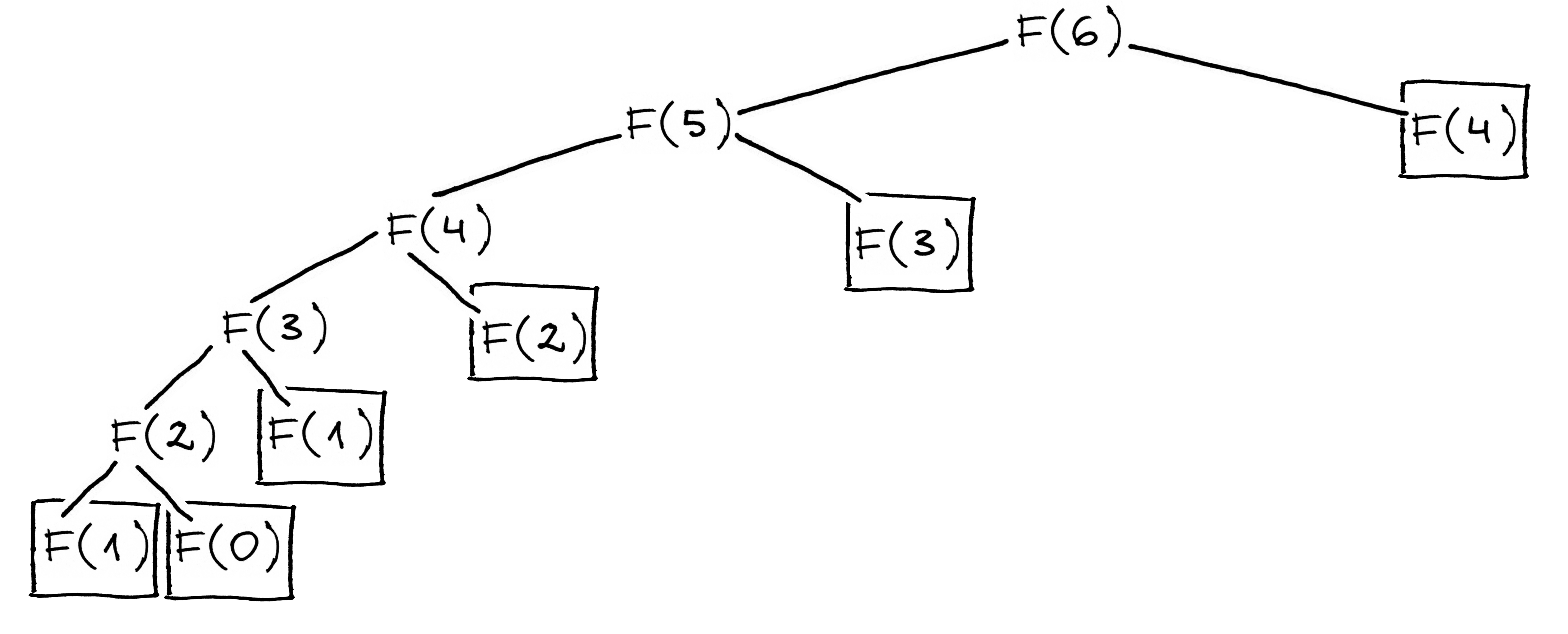
Fig. 72 Funkcijos F, įsimenančios tarpinius sprendinius,
skaičiavimų medis, kai į ją kreiptasi F(6)¶
Kiekviena reikšmė bus skaičiuojama tik vieną kartą, todėl
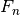 suskaičiuojamas per
suskaičiuojamas per 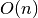 laiko. Tačiau dar
paprasčiau yra apsieiti be rekursijos ir suskaičiuoti
laiko. Tačiau dar
paprasčiau yra apsieiti be rekursijos ir suskaičiuoti 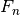 generuojant Fibonačio skaičių seką iš eilės, kiekvieną narį
gaunant iš dviejų paskutinių:
generuojant Fibonačio skaičių seką iš eilės, kiekvieną narį
gaunant iš dviejų paskutinių:
var Fmas : array [0..MAX] of longint;
function F(n : longint) : longint;
var k : integer;
begin
Fmas[0] := 0;
Fmas[1] := 1;
for k := 2 to n do
Fmas[k] := Fmas[k - 1] + Fmas[k - 2];
F := Fmas[n];
end;
const int MAX = ...;
long long Fmas[MAX+1];
long long F (long long n) {
Fmas[0] = 0;
Fmas[1] = 1;
for (int k = 2; k <= n; k++)
Fmas[k] = Fmas[k-1] + Fmas[k-2];
return Fmas[n];
}
Šioje funkcijoje 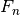 reikšmė skaičiuojama iš apačios į
viršų, t. y. pradedant nuo pačių mažiausių reikšmių ir vis
gaunant didesnes. Prieš tai aprašytos funkcijos reikšmes skaičiavo
iš viršaus į apačią.
reikšmė skaičiuojama iš apačios į
viršų, t. y. pradedant nuo pačių mažiausių reikšmių ir vis
gaunant didesnes. Prieš tai aprašytos funkcijos reikšmes skaičiavo
iš viršaus į apačią.
Tai, ką atlikome, buvo trečiasis dinaminio programavimo metodo žingsnis: rekursyvus apibrėžimas padėjo sukonstruoti efektyvų algoritmą. Efektyvumą (laiko atžvilgiu) pasiekėme atmetę pakartotinį tų pačių uždavinių sprendimą, įsimindami jų vertes (taigi atminties efektyvumo sąskaita 1).Tai būdinga visiems dinaminiu programavimu pagrįstiems algoritmams.
Jau buvo minėta, kad dinaminio programavimo išmokstama ne skaitant teoriją, o analizuojant sprendimus, tad tolesniuose skyreliuose ir analizuosime uždavinius, sprendžiamus dinaminio programavimo metodu.
Pradėsime nuo uždavinio, su kurio sąlyga jau esame susipažinę.
Kuprinės uždavinys¶
Vagis, naktį įsilaužęs į muziejų, rado
vertingų eksponatų. Žinoma kiekvieno eksponato vertė
bei svoris
, išreikšti sveikaisiais skaičiais. Vagis gali panešti kuprinę, sveriančią ne daugiau kaip
kilogramų.
Užduotis. Reikia nustatyti, kuriuos eksponatus jis turėtų susikrauti į kuprinę, kad bendra jų vertė būtų kuo didesnė, o kuprinė – panešama.
Tai klasikinis optimizavimo uždavinys, sprendžiamas optimizuojant
(pavyzdžiui, minimizuojant arba maksimizuojant) pasirinkto svorio
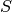 kuprinės vertę.
kuprinės vertę.
Uždavinį būtų galima spręsti perrinkimu – išbandyti visus
įmanomus rinkinius – tačiau tai, be abejo, labai neefektyvu.
Pastebėkime, kad nors galimų rinkinių labai daug (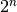 ),
tačiau galimų rinkinių svorių pakankamai nedaug – nuo 0 iki
),
tačiau galimų rinkinių svorių pakankamai nedaug – nuo 0 iki
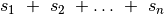 . Pasinaudosime šia savybe ir
sudarysime efektyvų, dinaminiu programavimu pagrįstą algoritmą.
. Pasinaudosime šia savybe ir
sudarysime efektyvų, dinaminiu programavimu pagrįstą algoritmą.
Dinaminio programavimo taikymas prasideda nuo optimalaus sprendinio
struktūros nustatymo. Sunumeruokime eksponatus nuo 1 iki  ir
pagalvokime, kokią didžiausią vertę galima pasiekti neviršijant
svorio
ir
pagalvokime, kokią didžiausią vertę galima pasiekti neviršijant
svorio 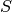 .
.  -asis eksponatas gali priklausyti arba
nepriklausyti optimaliam sprendiniui:
-asis eksponatas gali priklausyti arba
nepriklausyti optimaliam sprendiniui:
jei
 -asis eksponatas nepriklauso optimaliam sprendiniui, tai
optimalus sprendinys lygus kito, mažesnio uždavinio – optimalaus
rinkinio iš pirmųjų
-asis eksponatas nepriklauso optimaliam sprendiniui, tai
optimalus sprendinys lygus kito, mažesnio uždavinio – optimalaus
rinkinio iš pirmųjų 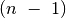 eksponatų, neviršijančio
svorio
eksponatų, neviršijančio
svorio 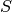 – sprendiniui;
– sprendiniui;jei
 -asis eksponatas priklauso optimaliam sprendiniui, tai
optimalų sprendinį sudaro
-asis eksponatas priklauso optimaliam sprendiniui, tai
optimalų sprendinį sudaro  -asis eksponatas ir kito,
mažesnio, uždavinio – optimalaus rinkinio iš pirmųjų
-asis eksponatas ir kito,
mažesnio, uždavinio – optimalaus rinkinio iš pirmųjų
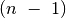 eksponatų, neviršijančio svorio
eksponatų, neviršijančio svorio
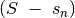 – sprendinys.
– sprendinys.
Tai ir yra optimalaus kuprinės uždavinio sprendinio struktūra. Optimalų sprendinį gausime išnagrinėję abu variantus ir išsirinkę didesnės vertės sprendinį.
Pažymėkime 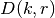 didžiausią rinkinio, kurio svoris
neviršija
didžiausią rinkinio, kurio svoris
neviršija  ir kuris sudarytas iš pirmųjų
ir kuris sudarytas iš pirmųjų  eksponatų, vertę. Tuomet, remdamiesi ankstesniais samprotavimais,
eksponatų, vertę. Tuomet, remdamiesi ankstesniais samprotavimais,
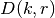 galime išreikšti rekursyviai:
galime išreikšti rekursyviai:
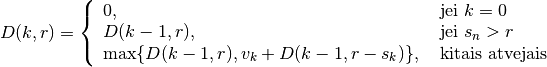
Ši formulė jau leidžia apskaičiuoti optimalaus sprendinio vertę
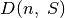 , tačiau efektyviai galime skaičiuoti tik įsimindami
dalinių sprendinių vertes (kaip ir Fibonačio skaičių atveju).
, tačiau efektyviai galime skaičiuoti tik įsimindami
dalinių sprendinių vertes (kaip ir Fibonačio skaičių atveju).
Panagrinėkime konkretų pavyzdį. Sakykime, vagis gali panešti 12 kilogramų. Eksponatų svoriai bei vertės pateikti lentelėje:
Eksponatas |
Vertė |
Svoris |
1 |
1 |
1 |
2 |
5 |
2 |
3 |
8 |
3 |
4 |
11 |
4 |
5 |
20 |
7 |
Paruošiame funkcijos 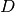 reikšmių lentelę, užpildydami iš
anksto žinomas kraštines reikšmes: maksimali vertė visada lygi
nuliui, kai nėra nė vieno eksponato (
reikšmių lentelę, užpildydami iš
anksto žinomas kraštines reikšmes: maksimali vertė visada lygi
nuliui, kai nėra nė vieno eksponato (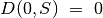 ), arba kai
vagis negali panešti jokio svorio (
), arba kai
vagis negali panešti jokio svorio (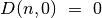 ).
).
Skaičiuojant 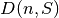 reikšmę pagal rekurentinį sąryšį,
naudojamos funkcijos reikšmės su mažesniais parametrais (t. y.
analogiškų uždavinių su mažesniais parametrais optimalūs
sprendiniai). Todėl jei lentelę pildysime po eilutę, pradėdami nuo
reikšmę pagal rekurentinį sąryšį,
naudojamos funkcijos reikšmės su mažesniais parametrais (t. y.
analogiškų uždavinių su mažesniais parametrais optimalūs
sprendiniai). Todėl jei lentelę pildysime po eilutę, pradėdami nuo
 , o eilutėje – iš kairės į dešinę, pradėdami nuo
, o eilutėje – iš kairės į dešinę, pradėdami nuo
 , tai skaičiuodami konkrečią reikšmę
(
, tai skaičiuodami konkrečią reikšmę
(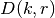 ) tikrai būsime jau anksčiau apskaičiavę kitas
reikalingas reikšmes (
) tikrai būsime jau anksčiau apskaičiavę kitas
reikalingas reikšmes (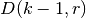 ir
ir 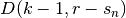 ).
).
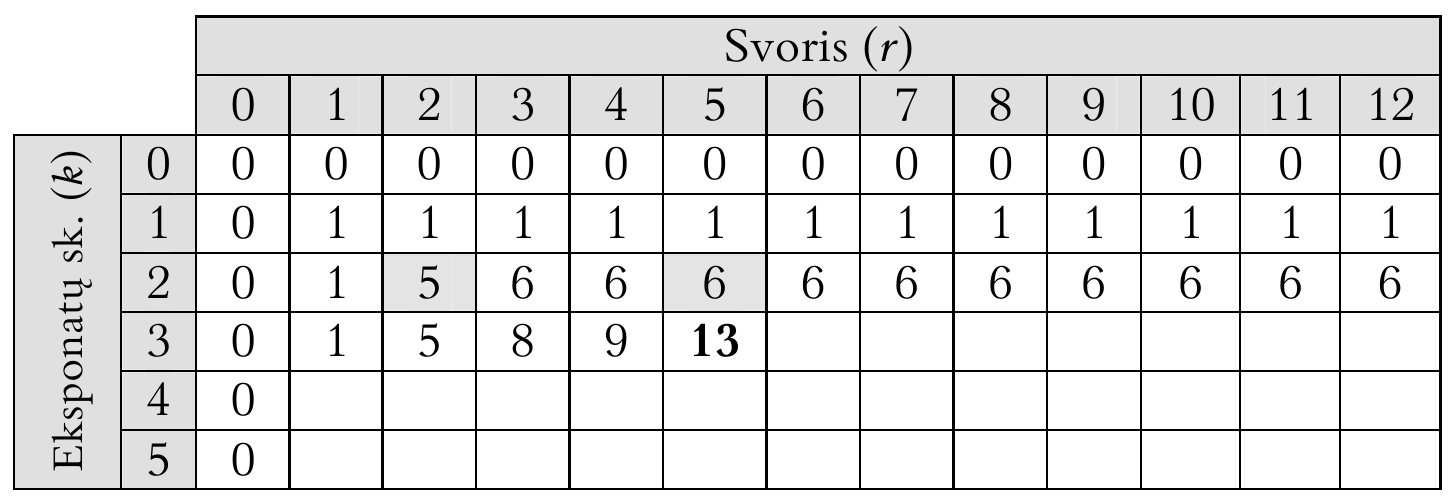
Pavyzdžiui, apskaičiuokime langelio 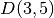 reikšmę, t. y.
raskime, kokia gali būti didžiausia kuprinėje esančių eksponatų
vertė, jei galime rinktis iš trijų pirmųjų eksponatų, o kuprinės
svoris negali viršyti 5 kg.
reikšmę, t. y.
raskime, kokia gali būti didžiausia kuprinėje esančių eksponatų
vertė, jei galime rinktis iš trijų pirmųjų eksponatų, o kuprinės
svoris negali viršyti 5 kg.
Galimi du variantai: arba įtraukti į rinkinį trečiąjį eksponatą, arba
ne. Pirmuoju atveju gausime vertę
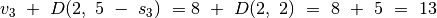 , o
antruoju –
, o
antruoju – 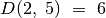 (skaičiavimams reikalingos
reikšmės lentelėje pažymėtos pilku fonu). Renkamės didesniąją
iš šių verčių – 13, trečiąjį eksponatą įtraukdami į
optimalų rinkinį.
(skaičiavimams reikalingos
reikšmės lentelėje pažymėtos pilku fonu). Renkamės didesniąją
iš šių verčių – 13, trečiąjį eksponatą įtraukdami į
optimalų rinkinį.
Taigi reikšmių lentelės užpildymą realizuoti nesudėtinga.
Programoje einamąją eilutę (eksponatų kiekį) žymėsime raide
 , einamąjį stulpelį (nagrinėjamą svorį) –
, einamąjį stulpelį (nagrinėjamą svorį) –  , o
eksponatų svorius ir vertes saugosime masyvuose
, o
eksponatų svorius ir vertes saugosime masyvuose svoris ir
vertė. Skaičiuodami konkretaus langelio [k, r] reikšmę, iš
pradžių patikriname, ar  -ojo eksponato svoris neviršija
nagrinėjamo svorio, t. y. ar
-ojo eksponato svoris neviršija
nagrinėjamo svorio, t. y. ar svoris[k] <= r. Jei viršija –
tai D[k, r] = D[k - 1, r], t. y.  -ojo eksponato į
rinkinį įtraukti negalime. Priešingu atveju,
-ojo eksponato į
rinkinį įtraukti negalime. Priešingu atveju, D[k, r] priskiriame
didesnę iš reikšmių D[k - 1, r] ir
(vertė[k] + D[k – 1, r – svoris[k]]).
const MAXN = ...; { maksimalus eksponatų skaičius }
MAXS = ...; { maksimalus panešamas svoris }
type lentelė = array [0..MAXN, 0..MAXS] of integer;
masyvas = array [1..MAXN] of integer;
procedure skaičiuok(n, S : integer;
var svoris, vertė : masyvas;
var D : lentelė);
var k, r : integer;
begin
{ užpildomos kraštinės lentelės reikšmės }
for r := 0 to S do
D[0, r] := 0;
for k := 0 to n do
D[k, 0] := 0;
{ užpildoma visa likusi lentelės dalis }
for r := 1 to S do
for k := 1 to n do
if svoris[k] <= r then
{ jei k-asis eksponatas tilptų }
D[k, r] := max (
D[k - 1, r],
vertė[k] + D[k - 1, r - svoris[k]])
{ Funkcija max randa didesnįjį iš dviejų
skaičių, jos teksto nepateikiame. }
else
{ jei k-asis eksponatas netilptų,
jo įtraukti negalima }
D[k, r] := D[k - 1, r];
end;
const int MAXN = ...; // maksimalus eksponatų skaičius
MAXS = ...; // maksimalus panešamas svoris
int n;
int S;
int svoris[MAXN+1];
int verte[MAXN+1];
int dp[MAXN+1][MAXS+1]; // knygoje šis masyvas žymimas "D", tačiau žymėti "dp" yra labiau įprasta
void skaiciuok () {
// užpildomos kraštinės lentelės reikšmės
for (int r = 0; r <= S; r++)
dp[0][r] = 0;
for (int k = 0; k <= n; k++)
dp[k][0] = 0;
// užpildoma visa likusi lentelės dalis
for (int r = 1; r <= S; r++) {
for (int k = 1; k <= n; k++) {
if (svoris[k] <= r)
// jei k-asis eksponatas tilptų
dp[k][r] = max(
dp[k-1][r], // k-ojo daikto neimame - svorį r turime gauti iš pirmų k-1 daiktų
verte[k-1] + dp[k-1][r-svoris[k]] // k-ąjį daiktą imame - tuomet pridedama jo vertė ir iš pirmų k-1 daiktų reikia surinkti svorį r-svoris[k]
);
else
// jei k-asis eksponatas netilptų, jo įtraukti negalima
dp[k][r] = dp[k-1][r];
}
}
}
Štai kaip atrodo iki galo užpildyta nagrinėto pavyzdžio lentelė Pusjuodžiu šriftu pažymėtos reikšmės, gaunamos įtraukiant atitinkamą eksponatą į rinkinį.
Taigi įvykdėme jau tris iš keturių dinaminio programavimo metodo
žingsnių: nustatę optimalią sprendinio struktūrą, išreiškėme jo
reikšmę rekursyviai ir sudarėme efektyvų algoritmą, kuris,
įsimindamas tarpinius sprendinius, apskaičiuoja šią reikšmę. Duoto
pavyzdžio atveju maksimali vertė lygi 33. Tačiau vagį, be abejo,
domina ne tik vertė, bet ir pats eksponatų rinkinys, kuris sudarytų
tokią vertę. Rinkinį nesudėtinga sukonstruoti iš jau suskaičiuotos
lentelės. Pradėkime nuo langelio [n, S]: jei
D[n, S] = D[n - 1, S], tai  -ojo eksponato į rinkinį
įtraukti nereikia (
-ojo eksponato į rinkinį
įtraukti nereikia (D[n, S] buvo gautas iš D[n - 1, S],
taigi neįtraukiant  -ojo eksponato), o jei
-ojo eksponato), o jei
D[n, S] > D[n - 1, S] – įtraukti reikia. Toliau atitinkamai
nagrinėjame langelius [n - 1, S] arba
[n - 1, S - svoris[n]], ir taip toliau, kol pasiekiame lentelės
kraštą.
type logmas = array [1..MAXN] of boolean;
procedure sudaryk_rinkinį(n, S : integer;
var svoris : masyvas;
var D : lentelė;
var imti : logmas);
{ pagal masyvų „D“ ir „svoris“ reikšmes nustatoma,
kuriuos eksponatus verta imti }
var k, r : integer;
begin
for k := 1 to n do
imti[k] := false;
k := n;
r := S;
while (k > 0) and (r > 0) do begin
if D[k, r] > D[k - 1, r] then begin
{ vadinasi, vertė D[k, r] gauta įtraukus k-ąjį eksponatą }
imti[k] := true;
r := r - svoris[k];
end;
k := k - 1;
end;
end;
int n;
int S;
int svoris[MAXN+1];
int D[MAXN+1][MAXS+1];
bool imti[MAXN+1];
void sudarykRinkini () {
// pagal masyvų "D" ir "svoris" reikšmes nustatoma, kuriuos eksponatus verta imti
for (int k = 1; k <= n; k++)
imti[k] = false;
int k = n, r = S;
while (k > 0 && r > 0) {
if (D[k][r] > D[k-1][r]) {
// vadinasi, vertė D[k][r] gauta įtraukus k-ąjį eksponatą
imti[k] = true;
r -= svoris[k];
}
k--;
}
}
Šią procedūrą reikia kviesti įvykdžius procedūrą skaičiuok.
Nesudėtinga įvertinti algoritmo sudėtingumą: pildant
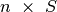 dydžio lentelę, kiekvienam langeliui sugaištama
dydžio lentelę, kiekvienam langeliui sugaištama
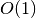 laiko, taigi algoritmo sudėtingumas ir atminties ir laiko
atžvilgiu yra
laiko, taigi algoritmo sudėtingumas ir atminties ir laiko
atžvilgiu yra 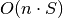 . Beje, jei pats rinkinys nedomina,
tai sudėtingumą atminties atžvilgiu galima sumažinti iki
. Beje, jei pats rinkinys nedomina,
tai sudėtingumą atminties atžvilgiu galima sumažinti iki
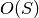 , kadangi skaičiuojant konkrečią reikšmę pakanka
prisiminti tik einamąją ir prieš tai buvusią lentelės eilutes.
Tačiau neapsigaukite: iš tiesų algoritmo sudėtingumas yra
polinominis tik jei iš anksto žinoma, jog dydis
, kadangi skaičiuojant konkrečią reikšmę pakanka
prisiminti tik einamąją ir prieš tai buvusią lentelės eilutes.
Tačiau neapsigaukite: iš tiesų algoritmo sudėtingumas yra
polinominis tik jei iš anksto žinoma, jog dydis 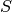 pakankamai
nedidelis. Bendru atveju (jei
pakankamai
nedidelis. Bendru atveju (jei 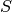 neapribotas),
Kuprinės uždavinys yra NP sunkus uždavinys.
neapribotas),
Kuprinės uždavinys yra NP sunkus uždavinys.
Uždavinys Ilgiausias didėjantis posekis¶
Duota
skaičių seka
.
Užduotis. Reikia rasti ilgiausią didėjantį šios sekos posekį.
Pavyzdžiui, jei duota seka (9, 5, 2, 8, 7, 3, 1, 6, 7, 4, 6, 3), tai ilgiausias didėjantis posekis turi keturis narius. Galimi sprendiniai (2, 3, 6, 7) arba (2, 3, 4, 6).
Pradėsime nuo optimalaus sprendinio struktūros nustatymo. Tai pavyks padaryti pradėjus analizuoti seką nuo pabaigos – tokia strategija dažnai pasiteisina (prisiminkime, jog Kuprinės uždavinyje ieškodami optimalaus sprendinio struktūros, eksponatus taip pat pradėjome analizuoti nuo paskutinio).
Tarkime, kad paskutinis sekos narys (skaičius 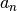 ) užbaigia
ilgiausią didėjantį posekį. Koks gi sekos narys posekyje eina prieš
) užbaigia
ilgiausią didėjantį posekį. Koks gi sekos narys posekyje eina prieš
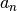 ? Tegu tai
? Tegu tai 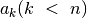 . Be abejo, tam, kad posekis
būtų didėjantis,
. Be abejo, tam, kad posekis
būtų didėjantis, 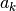 turi būti mažesnis už
turi būti mažesnis už 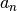 . Be
to,
. Be
to, 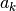 turi būti toks sekos narys, kad savo ruožtu sekoje
turi būti toks sekos narys, kad savo ruožtu sekoje
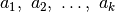 užbaigtų kuo ilgesnį didėjantį
posekį.
užbaigtų kuo ilgesnį didėjantį
posekį.
Pasitelkę tokius samprotavimus, uždavinio sprendinį išreiškėme
mažesnių uždavinių sprendiniais: jei visiems
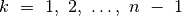 , kuriems
, kuriems 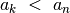 ,
žinotume, koks ilgiausio sekos
,
žinotume, koks ilgiausio sekos 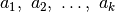 posekio,
užsibaigiančio nariu
posekio,
užsibaigiančio nariu 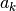 , ilgis, tai iš šių posekių
išrinkę ilgiausią ir prijungę
, ilgis, tai iš šių posekių
išrinkę ilgiausią ir prijungę 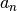 , tikrai gautume ilgiausią
didėjantį posekį, užsibaigiantį nariu
, tikrai gautume ilgiausią
didėjantį posekį, užsibaigiantį nariu 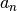 (kadangi būtume
išbandę visus variantus).
(kadangi būtume
išbandę visus variantus).
Jei kiekvienam sekos nariui suskaičiuotume, kokį ilgiausią didėjantį posekį šis užbaigia, tai iš jų išrinkę ilgiausią ir gautume ilgiausią didėjantį visos sekos posekį.
Pažymėję ilgiausio posekio, užsibaigiančio nariu 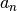 , ilgį
, ilgį
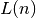 , ankstesnius samprotavimus galime užrašyti tokia lygybe:
, ankstesnius samprotavimus galime užrašyti tokia lygybe:
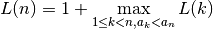
Rekursinis optimalios sprendinio vertės apibrėžimas yra antrasis dinaminio programavimo metodo žingsnis. Pagal šią formulę sudarysime efektyvų algoritmą.
Toliau pateikiama procedūra rasti optimaliam sprendiniui iš apačios
į viršų. Iš pradžių randama, kokį ilgiausią posekį užbaigia
sekos narys 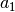 , tuomet
, tuomet 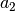 , ir taip toliau iki
, ir taip toliau iki
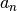 . Iš šių išrenkamas ilgiausias visos sekos posekis.
Atskirame masyve
. Iš šių išrenkamas ilgiausias visos sekos posekis.
Atskirame masyve p saugoma informacija, kuri vėliau padės
sukonstruoti optimalų sprendinį: p[k] rodo ilgiausio sekos
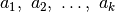 posekio, užsibaigiančio nariu
posekio, užsibaigiančio nariu
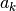 , priešpaskutinio nario numerį.
, priešpaskutinio nario numerį.
const MAX = ...; { maksimalus sekos ilgis }
type masyvas = array [1..MAX] of integer;
procedure ilg_posekis(a : masyvas; n : integer;
var posekis : masyvas;
var ilgis : integer);
var L, p : masyvas;
k, kmax, m, nr : integer;
begin
{ optimalaus sprendinio vertė skaičiuojama iš apačios į viršų }
kmax := 1; { ilgiausio posekio paskutiniojo elemento indeksas }
for m := 1 to n do begin
L[m] := 0;
for k := 1 to m - 1 do
if (a[k] < a[m]) and (L[k] > L[m])
then begin
L[m] := L[k];
{pažymimas priešpaskutinis šio posekio elementas}
p[m] := k;
end;
{ priskaičiuojamas ir m-asis elementas }
L[m] := L[m] + 1;
if L[kmax] < L[m] then
{ tai ilgiausias kol kas rastas posekis }
kmax := m;
end;
{ sukonstruojamas optimalus sprendinys }
ilgis := L[kmax];
for k := ilgis downto 1 do begin
posekis[k] := a[kmax];
kmax := p[kmax];
end;
end;
const int MAX = ...; // maksimalus sekos ilgis
int n;
int a[MAX+1];
int posekis[MAX+1];
int ilgis;
void ilgPosekis () {
int L[MAX+1];
int p[MAX+1];
// optimalaus sprendinio vertė skaičiuojama iš apačios į viršų
int kmax = 1;
for (int m = 1; m <= n; m++) {
for (int k = 1; k < m; k++) {
if (a[k] < a[m] && L[k] > L[m]) {
L[m] = L[k];
// pažymimas priešpaskutinis šio posekio elementas
p[m] = k;
}
}
// priskaičiuojamas ir m-asis elementas
L[m]++;
if (L[kmax] < L[m])
// tai ilgiausias kol kas rastas posekis
kmax = m;
}
// sukonstruojamas optimalus sprendinys
ilgis = L[kmax];
for (int k = ilgis; k > 0; k--) {
posekis[k] = a[kmax];
kmax = p[kmax];
}
}
Šio sprendimo sudėtingumas laiko atžvilgiu yra 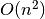 , o
atminties atžvilgiu –
, o
atminties atžvilgiu – 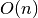 .
.
Parodysime, kaip randamas ilgiausias sąlygoje pateiktos sekos (9, 5, 2, 8, 7, 3, 1, 6, 7, 4, 6, 3) posekis.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
9 |
5 |
2 |
8 |
7 |
3 |
1 |
6 |
7 |
4 |
6 |
3 |
|
1 |
1 |
1 |
2 |
2 |
2 |
1 |
3 |
4 |
3 |
4 |
2 |
|
– |
– |
– |
2 |
2 |
3 |
– |
6 |
8 |
6 |
10 |
3 |
Kaip minėta pavyzdyje, yra du ilgiausi didėjantys posekiai, kurių
ilgis 4 – eilutėje 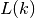 skaičius 4 įrašytas dviejuose
langeliuose. Pasinaudojus masyvo
skaičius 4 įrašytas dviejuose
langeliuose. Pasinaudojus masyvo p reikšmėmis nesunku sukonstruoti
patį posekį. Pavyzdžiui, konstruosime posekį, užsibaigantį
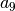 . Paskutinis posekio narys yra
. Paskutinis posekio narys yra 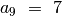 ,
priešpaskutinio posekio nario numeris lygus
,
priešpaskutinio posekio nario numeris lygus 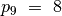 , tad šis
narys lygus
, tad šis
narys lygus 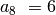 . Prieš jį eina šeštas
(
. Prieš jį eina šeštas
(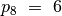 ) sekos narys
) sekos narys 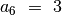 , o prieš šį
trečias –
, o prieš šį
trečias – 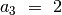 . Taigi ilgiausias didėjantis
nagrinėtos sekos posekis yra (2, 3, 6, 7).
. Taigi ilgiausias didėjantis
nagrinėtos sekos posekis yra (2, 3, 6, 7).
Uždavinys Teisingos dalybos 2¶
Dvi draugės – Rusnė ir Emilija – nori pasidalyti
dovanų rinkinį. Kiekviena dovana turi būti atiduota arba Rusnei, arba Emilijai, ir nė viena dovana negali būti padalyta į dvi dalis. Kiekviena dovana turi vertę, išreikštą sveikuoju skaičiumi nuo 0 iki
. Pažymėkime
ir
dovanų, kurias atitinkamai gaus Rusnė ir Emilija, verčių sumas.
Užduotis. Reikia rasti, kaip padalyti dovanas Rusnei ir Emilijai, kad
būtų minimalus.
Dovanų vertes pažymėkime 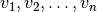 . Bendra šių
dovanų vertė lygi
. Bendra šių
dovanų vertė lygi 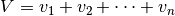 . Atkreipkite
dėmesį, kad
. Atkreipkite
dėmesį, kad 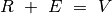 . Taigi, žinodami vieną iš šių
skaičių, galime iš karto apskaičiuoti ir antrą. Taip pat žinant,
kurios dovanos bus atiduotos Rusnei, vienareikšmiškai galima pasakyti,
kurios atiteks Emilijai. Taigi galima spręsti „pusę“ uždavinio:
ieškoti, kaip parinkti dovanas Rusnei, kad jų verčių suma būtų kuo
artimesnė
. Taigi, žinodami vieną iš šių
skaičių, galime iš karto apskaičiuoti ir antrą. Taip pat žinant,
kurios dovanos bus atiduotos Rusnei, vienareikšmiškai galima pasakyti,
kurios atiteks Emilijai. Taigi galima spręsti „pusę“ uždavinio:
ieškoti, kaip parinkti dovanas Rusnei, kad jų verčių suma būtų kuo
artimesnė 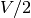 .
.
Šį kartą dinaminį programavimą taikysime netiesiogiai: iš pradžių dinaminiu programavimu išspręsime kitą uždavinį, vadinamą sumos dėstymu, o pasinaudoję jo sprendimu, nesunkiai padalysime dovanas mergaitėms teisingiausiu įmanomu būdu.
Tarkime, duota  sveikųjų skaičių
sveikųjų skaičių
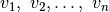 iš intervalo
iš intervalo ![[0, m]](_images/math/ece04a7cc093dab002503e5ba474809c2d3079e0.png) . Prašoma
nustatyti, ar (ir kaip) iš jų galima sudaryti tokį skaičių
rinkinį, kad jų suma būtų lygi
. Prašoma
nustatyti, ar (ir kaip) iš jų galima sudaryti tokį skaičių
rinkinį, kad jų suma būtų lygi 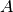 . Jei taip, tai sakysime,
kad iš skaičių
. Jei taip, tai sakysime,
kad iš skaičių 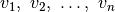 galime sudėti
skaičių
galime sudėti
skaičių 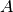 . Šis uždavinys vadinamas sumos dėstymu.
. Šis uždavinys vadinamas sumos dėstymu.
Nesunku pastebėti, kad išsprendę sumos dėstymo uždavinį, mokėsime
išspręsti ir Teisingų dalybų uždavinį: iš dovanų verčių
paeiliui bandysime sudėti skaičius, kuo artimesnius 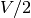 , ir
sustosime, kai tik pavyks.
, ir
sustosime, kai tik pavyks.
Galimų rinkinių yra labai daug – 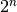 , jų visų išbandyti
negalima. Kita vertus, sumų, kurias gali sudaryti kuris nors duotųjų
skaičių rinkinys, yra palyginti nedaug – tai skaičiai nuo 0 iki
, jų visų išbandyti
negalima. Kita vertus, sumų, kurias gali sudaryti kuris nors duotųjų
skaičių rinkinys, yra palyginti nedaug – tai skaičiai nuo 0 iki
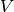 , kur
, kur 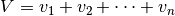 , taigi jų ne daugiau
negu
, taigi jų ne daugiau
negu 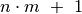 .
.
Pasinaudoję šia savybe, sudarysime dinaminiu programavimu pagrįstą algoritmą.
Tarkime, kad iš duotųjų  skaičių galima sudėti skaičių
skaičių galima sudėti skaičių
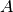 . Skaičius
. Skaičius 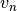 gali priklausyti šiam rinkiniui arba
nepriklausyti (kitų variantų nėra):
gali priklausyti šiam rinkiniui arba
nepriklausyti (kitų variantų nėra):
jei skaičius
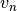 rinkiniui nepriklauso, tai skaičių
rinkiniui nepriklauso, tai skaičių
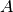 turi būti įmanoma sudėti iš pirmųjų
turi būti įmanoma sudėti iš pirmųjų 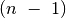 skaičių;
skaičių;jei
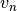 rinkiniui priklauso, tai iš pirmųjų
rinkiniui priklauso, tai iš pirmųjų
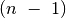 skaičių turi būti įmanoma sudėti likusią
skaičiaus dalį
skaičių turi būti įmanoma sudėti likusią
skaičiaus dalį 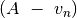 .
.
Taigi abiem atvejais uždavinį galima išreikšti per analogiškų,
tačiau su mažesniais parametrais, uždavinių sprendimus. Jei teiginį
„skaičių 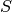 galima sudėti iš pirmųjų
galima sudėti iš pirmųjų  skaičių“ pažymėsime
skaičių“ pažymėsime 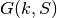 , tai būtų teisingos tokios
lygybės 3:
, tai būtų teisingos tokios
lygybės 3:
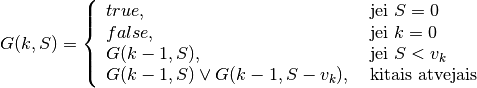
Remiantis šiomis lygybėmis nesunku sudaryti efektyvų Sumos dėstymo
uždavinio algoritmą – apskaičiuoti funkcijos 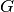 reikšmes
iš apačios į viršų, pildant
reikšmes
iš apačios į viršų, pildant 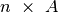 dydžio reikšmių
lentelę, pradedant nuo mažiausių
dydžio reikšmių
lentelę, pradedant nuo mažiausių  (taip, kaip darėme
spręsdami Kuprinės uždavinį).
(taip, kaip darėme
spręsdami Kuprinės uždavinį).
Pavyzdžiui, jei duotieji skaičiai yra 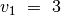 ,
,
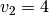 ,
, 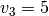 ,
, 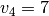 ir klausiama, ar iš
jų galima sudėti skaičių
ir klausiama, ar iš
jų galima sudėti skaičių 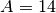 , tai reikšmių lentelė,
gauta iš rekurentinių lygybių, būtų tokia (pažymėtos tik
teigiamos funkcijos reikšmės):
, tai reikšmių lentelė,
gauta iš rekurentinių lygybių, būtų tokia (pažymėtos tik
teigiamos funkcijos reikšmės):
Pildant lentelės langelį ![[k, S]](_images/math/af061b00303fe8e4020314d7fd616df2e2619d90.png) , peržiūrimi langeliai
, peržiūrimi langeliai
![[k - 1, S]](_images/math/5b6f67995834aeb297807433928be724029a9657.png) ir
ir ![[k - 1, S - v_k]](_images/math/47da7da23876b7ce9c80a1b1fb59fcd24b621bef.png) : jei bent viename
iš jų įrašyta reikšmė
: jei bent viename
iš jų įrašyta reikšmė 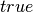 , tai į
, tai į ![[k, S]](_images/math/020972c4fc54647be62a16dae4e404f3fe144f4c.png) taip
pat įrašoma
taip
pat įrašoma 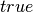 :
:
const MAXN = ...; { maksimalus dėmenų skaičius }
MAXM = ...; { maksimali dėmens vertė }
type masyvas = array [1..MAXN] of integer;
logmas2 = array [0..MAXN * MAXM,
0..MAXN] of boolean;
procedure dėstyk(var v : masyvas; n, A : integer;
var G : logmas2);
var k, S : integer;
begin
{ išvalomos masyvo reikšmės }
for k := 0 to n do
for S := 0 to A do
G[k, S] := false;
{ išdėstomos sumos }
G[0, 0] := true; { inicializuojama kraštiė reikšmė }
for k := 1 to n do
for S := 0 to A do
if G[k - 1, S] then
G[k, S] := true
else if (v[k] <= S) then
if (G[k - 1, S - v[k]]) then
G[k, S] := true;
end;
const int MAXN = ...; // maksimalus dėmenų skaičius
const int MAXM = ...; // maksimali dėmens vertė
int n;
int A;
int v[MAXN+1];
bool G[MAXN*MAXM+1][MAXN+1];
void destyk () {
// išvalomos masyvo reikšmės
for (int k = 0; k <= n; k++)
for (int S = 0; S <= A; S++)
g[k][s] = false;
// išdėstomos sumos
G[0][0] = true; // inicializuojama kraštinė reikšmė
for (int k = 1; k <= n; k++) {
for (int S = 0; S <= A; S++) {
if (G[k-1][S])
G[k][S] = true;
else if (v[k] <= S) {
if (G[k-1][S-v[k]])
G[k][S] = true;
}
}
}
}
Algoritmo sudėtingumas atminties ir laiko atžvilgiu yra vienodas –
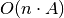 .
.
Dabar galime grįžti prie Teisingų dalybų uždavinio. Pasinaudoję
dinaminiu programavimu pagrįstu sumos dėstymo algoritmu, efektyviai
apskaičiuosime, kokių verčių dovanų rinkinius įmanoma sudaryti.
Iš šių rinkinių pakanka išrinkti tą, kurio vertė artimiausia
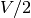 (visų verčių sumos pusei). Belieka pasinaudoti
apskaičiuotais duomenimis (masyvu
(visų verčių sumos pusei). Belieka pasinaudoti
apskaičiuotais duomenimis (masyvu 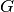 ) ir pasirinkti, kurias
dovanas reikia skirti Rusnei, o kurias – Emilijai. Sumos dėstymo
uždavinio terminais tai reikštų nustatyti, kuriuos iš
) ir pasirinkti, kurias
dovanas reikia skirti Rusnei, o kurias – Emilijai. Sumos dėstymo
uždavinio terminais tai reikštų nustatyti, kuriuos iš  dėmenų reikia sudėti, norint gauti skaičių A. Tad nagrinėjame
lentelės langelį
dėmenų reikia sudėti, norint gauti skaičių A. Tad nagrinėjame
lentelės langelį ![G[n, A]](_images/math/d7f4326eb67dd1812197f59ff662bbc1cd514515.png) :
:  -asis dėmuo
nereikalingas, jei
-asis dėmuo
nereikalingas, jei 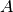 galima sudėti iš likusių
galima sudėti iš likusių 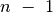 dėmenų, t. y.
dėmenų, t. y. ![G[n - 1, A] = true](_images/math/7739ffeaf08f1e0996d738fb214b934ddeb46a80.png) . Priešingu atveju,
. Priešingu atveju,
 -asis narys būtinas. Toliau analogiškai tikriname
-asis narys būtinas. Toliau analogiškai tikriname
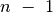 dėmens reikalingumą, nagrinėdami langelius
dėmens reikalingumą, nagrinėdami langelius
![G[n - 1, A]](_images/math/c45d25a700f1b97a86dd80a5283a0e893220e923.png) arba
arba ![G[n - 1, A - v_n]](_images/math/ea078c97d262967dce9c681cbfab5dbda636e6ca.png) .
.
type logmas = array [1..MAXN] of boolean;
procedure dalybos(var Rusnei : logmas;
var v : masyvas; n : integer);
{ rezultatas įrašomas į masyvą „Rusnei“: Rusnei[k] = true,
jei k-ąją dovaną reikia skirti jai }
var G : logmas2;
Vsum : longint;
i, S : integer;
begin
{ suskaičiuojama visų verčių suma }
Vsum := 0;
for i := 1 to n do
Vsum := Vsum + v[i];
dėstyk(v, n, Vsum div 2, G);
{ randama artimiausia V/2 reikšmė, kurią galima išdėstyti }
S := Vsum div 2;
while not G[n, S] do
S := S - 1;
{ nustatoma, kurias iš dovanų skirti Rusnei,
kad jų bendra vertė būtų lygi S }
for i := 1 to n do
Rusnei[i] := false;
i := n;
for i := n downto 1 do
{ tikrinama, ar S vertės rinkiniui priklauso i-oji dovana }
if not G[i - 1, S] then begin
Rusnei[i] := true;
S := S - v[i];
end;
end;
int n;
int A;
int v[MAXN+1];
int G[MAXN*MAXM+1][MAXN+1];
bool Rusnei[MAXN+1];
void dalybos () {
/*
rezultatas įrašomas į masyvą "Rusnei":
Rusnei[k] = true, jei k-ąją dovaną reikia skirti jai
*/
// suskaičiuojama visų verčių suma
long long Vsum = 0;
for (int i = 1; i <= n; i++)
Vsum += v[i];
A = Vsum/2;
destyk();
// randama artimiausia Vsum/2 reikšmė, kurią galima išdėstyti
int S = Vsum/2;
while (!G[n][S]) {
S--;
}
// nustatoma, kurias iš dovanų skirti Rusnei, kad jų bendra vertė būtų lygi S
for (int i = 1; i <= n; i++)
Rusnei[i] = false;
for (int i = n; i > 0; i--) {
// tikrinama, ar S vertės rinkiniui priklauso i-toji dovana
if (!G[i-1][S]) {
Rusnei[i] = true;
S -= v[i];
}
}
}
Šio sprendimo sudėtingumas sutampa su sumos dėstymo algoritmo
sudėtingumu, kur dėstoma suma 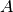 neviršija
neviršija 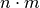 ,
taigi yra toks:
,
taigi yra toks: 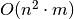 .
.
Uždavinys Bibliotekoje 4¶
bibliotekos darbuotojų buvo paskirta užduotis: peržiūrėti visas vienos lentynos knygas ieškant tam tikros informacijos. Šioje lentynoje iš viso yra
knygų. Darbą norima paskirstyti darbuotojams kuo lygesnėmis dalimis, tačiau knygos turėtų išlikti savo vietose, todėl buvo nuspręsta paprasčiausiai išskaidyti visą lentyną į
nesikertančių sričių, ir pavesti kiekvienam darbuotojui ieškoti informacijos tik vienoje srityje. Vis dėlto vienos knygos puslapių skaičiumi gerokai viršija kitas, todėl lentyną į
sričių norima išskaidyti optimaliai – taip, kad didžiausias vienam darbuotojui tenkantis puslapių skaičius būtų kuo mažesnis.
Užduotis. Duoti visų knygų puslapių skaičiai
. Reikia rasti, kaip visą darbą darbuotojams paskirstyti optimaliai.
Pradėkime analizuoti uždavinį nuo kelių paprastų pavyzdžių. Tegu visą darbą reikia padalyti trims darbuotojams, o lentynoje yra devynios knygos. Be abejo, jei visos knygos turėtų vienodą puslapių skaičių, tai lentyną galėtume skaidyti į tris lygias dalis:
100 100 100 | 100 100 100 | 100 100 100
Tačiau lentynos dalijimas lygiomis dalimis tikrai netikęs, jei puslapių skaičius knygose gerokai skiriasi:
100 200 300 | 400 500 600 | 700 800 900
Šiuo atveju pirmam darbuotojui tektų peržiūrėti
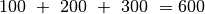 puslapių, o trečiajam –
puslapių, o trečiajam –
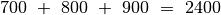 , taigi net keturis kartus daugiau.
Išbandę įvairius variantus, galime padaryti išvadą, kad geriausias
įmanomas paskirstymas būtų toks:
, taigi net keturis kartus daugiau.
Išbandę įvairius variantus, galime padaryti išvadą, kad geriausias
įmanomas paskirstymas būtų toks:
100 200 300 400 500 | 600 700 | 800 900
Tuomet darbuotojams tektų peržiūrėti atitinkamai 1500, 1300 ir 1700 puslapių.
Ar yra kokia nors strategija, kurios laikydamiesi lentynoje esančias
knygas visuomet padalytume optimaliai? Idealiu atveju visiems
darbuotojams darbas paskirstomas lygiomis dalimis, t. y. kiekvienam
darbuotojui tenkantis puslapių skaičius lygus visų knygų puslapių
skaičių sumai, padalytai iš darbuotojų skaičiaus:
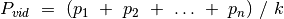 . Todėl būtų
natūralu apskaičiuoti šią reikšmę ir iš eilės parinkinėti
sritis, stengiantis jų dydžius gauti kuo artimesnius
. Todėl būtų
natūralu apskaičiuoti šią reikšmę ir iš eilės parinkinėti
sritis, stengiantis jų dydžius gauti kuo artimesnius 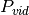 ,
t. y. taikyti godžiąją strategiją.
,
t. y. taikyti godžiąją strategiją.
Vadovaudamiesi šia strategija, gautume optimalų paskirstymą visuose kol kas nagrinėtuose pavyzdžiuose. Tačiau neskubėkime daryti išvadų. Bendru atveju galima gauti ir neoptimalų knygų paskirstymą: jei keliems darbuotojams skiriamas darbas yra šiek tiek mažesnis už vidurkį, tai paskutiniam gali susikaupti nemažai „papildomo“ darbo.
Tarkime, lentynoje iš eilės sudėtos 6 knygos po 80 puslapių, o
toliau trys knygos, kurių puslapių skaičiai lygūs 100, 30 ir 200, ir
jas reikia paskirstyti trims darbuotojams. Šiuo atveju
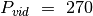 . Taigi vadovaudamiesi godžiąją strategija,
pirmam darbuotojui skirtume peržiūrėti pirmas tris knygas (240
puslapių yra artimesnė reikšmė
. Taigi vadovaudamiesi godžiąją strategija,
pirmam darbuotojui skirtume peržiūrėti pirmas tris knygas (240
puslapių yra artimesnė reikšmė 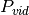 , negu 320), antram
– taip pat tris knygas, ir galų gale gautume tokį knygų
paskirstymą:
, negu 320), antram
– taip pat tris knygas, ir galų gale gautume tokį knygų
paskirstymą:
80 80 80 | 80 80 80 | 100 30 200
Daugiausiai darbo – 330 puslapių – tektų trečiajam darbuotojui. Tačiau optimaliu atveju didžiausias peržiūrimų puslapių skaičius būtų lygus 320:
80 80 80 80 | 80 80 100 | 30 200
Taigi optimalus paskirstymas gaunamas pirmajam darbuotojui skiriant keturias knygas. Godžioji strategija šito negalėjo numatyti, kadangi sprendimai priimami pagal labai paprastą kriterijų, nenumatant jų padarinių.
Sudarysime dinaminiu programavimu pagrįstą algoritmą šiam dalijimo uždaviniui spręsti. Jis visuomet ras optimalų paskirstymą, kadangi išanalizuos visus galimus variantus, tačiau tai atliks efektyviai.
Kad būtų paprasčiau, sutarsime knygų nuo 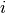 -osios iki
-osios iki
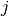 -osios puslapių skaičių sumą žymėti
-osios puslapių skaičių sumą žymėti 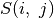 ,
t. y.
,
t. y. 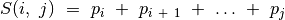 .
Didžiausią vienam darbuotojui peržiūrėti tenkantį puslapių
skaičių vadinsime paskirstymo įverčiu.
.
Didžiausią vienam darbuotojui peržiūrėti tenkantį puslapių
skaičių vadinsime paskirstymo įverčiu.
Taigi pradėkime nuo optimalios sprendinio struktūros nustatymo. Bet
kuriame paskirstyme  -ajam darbuotojui tenka kažkiek knygų iš
lentynos pabaigos, t. y. knygos nuo
-ajam darbuotojui tenka kažkiek knygų iš
lentynos pabaigos, t. y. knygos nuo 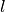 -iosios iki
-iosios iki
 -osios,
-osios, 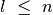 . Kad ir koks būtų paskirstymas,
daugiausiai darbo tenka arba
. Kad ir koks būtų paskirstymas,
daugiausiai darbo tenka arba  -ajam darbuotojui, arba kuriam
nors kitam. Pirmu atveju (jei daugiausia darbo tenka
-ajam darbuotojui, arba kuriam
nors kitam. Pirmu atveju (jei daugiausia darbo tenka  -ajam
darbuotojui), paskirstymo įvertis lygus
-ajam
darbuotojui), paskirstymo įvertis lygus 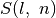 , o antruoju
atveju susiduriame su analogišku, tik mažesniu, uždaviniu –
optimaliu lentynos iki
, o antruoju
atveju susiduriame su analogišku, tik mažesniu, uždaviniu –
optimaliu lentynos iki 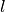 -osios knygos (jos neįtraukiant)
paskirstymu pirmiesiems
-osios knygos (jos neįtraukiant)
paskirstymu pirmiesiems 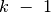 darbuotojų.
darbuotojų.
Pažymėkime optimalų  knygų paskirstymo
knygų paskirstymo  darbuotojų įvertį
darbuotojų įvertį 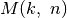 . Jei žinotume, kad optimalu
. Jei žinotume, kad optimalu
 -ajam darbuotojui skirti knygas nuo
-ajam darbuotojui skirti knygas nuo 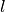 -osios iki
-osios iki
 -osios (t.y. žinotume, kam lygus
-osios (t.y. žinotume, kam lygus 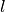 ), tai
), tai
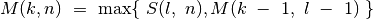
Tačiau mes iš anksto nežinome, kiek knygų optimalu skirti
paskutiniam darbuotojui. Todėl tenka išbandyti visus galimus variantus
ir pasirinkti tą, kurio atveju gaunamo paskirstymo įvertis yra
mažiausias. Taigi iš tiesų 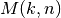 apibrėžiamas taip:
apibrėžiamas taip:
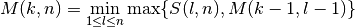
t. y. minimumas yra skaičiuojamas iš visų maksimumų, gaunamų, kai
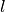 kinta nuo 1 iki
kinta nuo 1 iki  .
.
Kad funkcijos reikšmes galėtume skaičiuoti pagal rekursyvų
apibrėžimą, jį būtina papildyti kraštinėmis reikšmėmis:
paskirstymo įvertis visada lygus nuliui, jei lentyna tuščia; jei yra
tik vienas darbuotojas, tai jam atitenka visas darbas, kuris lygus
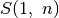 .
.
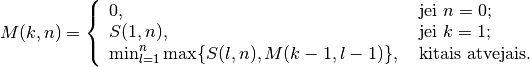
Rekursyviai apibrėžę optimalaus sprendinio vertę, jau galime
sudaryti ją efektyviai apskaičiuojantį algoritmą. Tačiau
nepamirškime, jog mus domina ne tik sprendinio vertė, bet ir pats
sprendinys, t. y. optimalus lentynos paskirstymas. Skirtingai nuo ligi
šiol nagrinėtų uždavinių, sprendinį sukonstruoti iš
apskaičiuotos funkcijos reikšmių lentelės būtų per sudėtinga.
Todėl skaičiuodami kaupsime papildomus duomenis: jei skaičiuodami
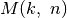 reikšmę nustatysime, kad
reikšmę nustatysime, kad  -ajam darbuotojui
optimalu paskirti knygas nuo
-ajam darbuotojui
optimalu paskirti knygas nuo 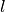 -osios iki
-osios iki  -osios, tai
dydį
-osios, tai
dydį 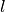 pasižymėsime atskirame masyve (
pasižymėsime atskirame masyve (D[k, n] := l).
Toliau pateikiamas procedūros, apskaičiuojančios, kaip optimaliai paskirstyti knygų peržiūrėjimo darbą darbuotojams, tekstas.
const MAXN = ...; { maksimalus knygų skaičius }
MAXK = ...; { maksimalus darbuotojų skaičius }
BEGALINIS = MAXINT;
type masyvas = array [0..MAXN + MAXK] of integer;
masyvas2 = array [1..MAXK, 0..MAXN] of integer;
procedure paskirstyk(k, n : integer;
p : masyvas; { psl. skaičius }
var įvertis : integer;
var nuo : masyvas);
{ apskaičiuoja knygų nuo i-osios iki j-osios puslapių skaičių sumą }
function S(i, j : integer) : integer;
var h : integer;
begin
S := 0;
for h := i to j do
S := S + p[h];
end;
var i, j, l, v : integer; { pagalbiniai kintamieji }
D, M : masyvas2;
begin
{ užpildomos kraštinės reikšmės }
for i := 1 to k do
M[i, 0] := 0;
for j := 1 to n do begin
M[1, j] := S(1, j);
D[1, j] := 1;
end;
{ apskaičiuojama likusi lentelės dalis }
for i := 2 to k do
for j := 1 to n do begin
M[i, j] := BEGALINIS;
{ renkamasis minimumas... }
for l := 1 to j do begin
{ ...iš maksimumų }
v := max(S(l, j), M[i - 1, l - 1]);
{ Funkcija max randa didesnįjį iš dviejų skaičių, jos
nepateiksime. }
if v < M[i, j] then begin
M[i, j] := v;
D[i, j] := l;
end;
end;
end;
{ sukonstruojamas optimalus sprendinys }
įvertis := M[k, n];
j := n;
for i := k downto 2 do begin
nuo[i] := D[i, j];
j := D[i, j] - 1;
{ jei i-ajam darbuotojui skiriamos knygos nuo D[i, j], tai
likusiems i – 1 darbuotojų reikia paskirstyti D[i, j] – 1 knygų}
end;
nuo[1] := 1;
end;
const int MAXN = ...; // maksimalus knygų skaičius
const int MAXK = ...; // maksimalus darbuotojų skaičius
const int BEGALINIS = ...; // kažkoks kuo didesnis skaičius, pavyzdžiui, 1e9
int k;
int n;
int p; // puslapių skaičius
int ivertis;
int nuo[MAXN+MAXK+1];
int S (int i, int j) {
// apskaičiuoja knygų nuo i-tosios iki j-tosios puslapių skaičių sumą
int suma = 0;
for (int h = i; h <= j; h++)
suma += p[h];
return suma;
}
void paskristyk () {
int D[MAXK+1][MAXN+1], M[MAXK+1][MAXN+1];
// užpildomos kraštinęs reikšmės
for (int i = 1; i <= k; i++)
M[i][0] = 0;
for (int j = 1; j <= n; j++) {
M[1][j] = S(1, j);
D[1][j] = 1;
}
// apskaičiuojama likusi lentelės dalis
for (int i = 2; i <= k; i++) {
for (int j = 1; j <= n; j++) {
M[i][j] = BEGALINIS;
// renkamas minimumas...
for (int l = 1; l <= j; l++) {
// ...iš maksimumų
v = max(S(l, j), M[i-1][l-1]);
if (v < M[i][j]) {
M[i][j] = v;
D[i][j] = l;
}
}
}
}
// sukonstruojamas optimalus sprendinys
ivertis = M[k][n];
int j = n;
for (int i = k; i > 1; i--) {
nuo[i] = D[i][j];
j = D[i][j]-1;
/*
jei i-tajam darbuotojui skiriamos knygos nuo D[i][j],
tai likusiems i-1 darbuotojų reikia paskirti
D[i][j]-1 knygų
*/
}
nuo[1] = 1;
}
Procedūra grąžina kelis rezultatus:
gautojo (optimalaus) paskirstymo įvertį, t. y. kiek daugiausiai darbo teks vienam iš darbuotojų;
lentynoje esančių knygų paskirstymą. Šis pateikiamas masyve
nuo. -ajam (bet kuriam, išskyrus paskutinį)
darbuotojui paskirtos knygos yra intervalas
-ajam (bet kuriam, išskyrus paskutinį)
darbuotojui paskirtos knygos yra intervalas
[nuo[j], nuo[j + 1]), o -ajam (paskutiniam) –
-ajam (paskutiniam) –
[nuo[k], n].
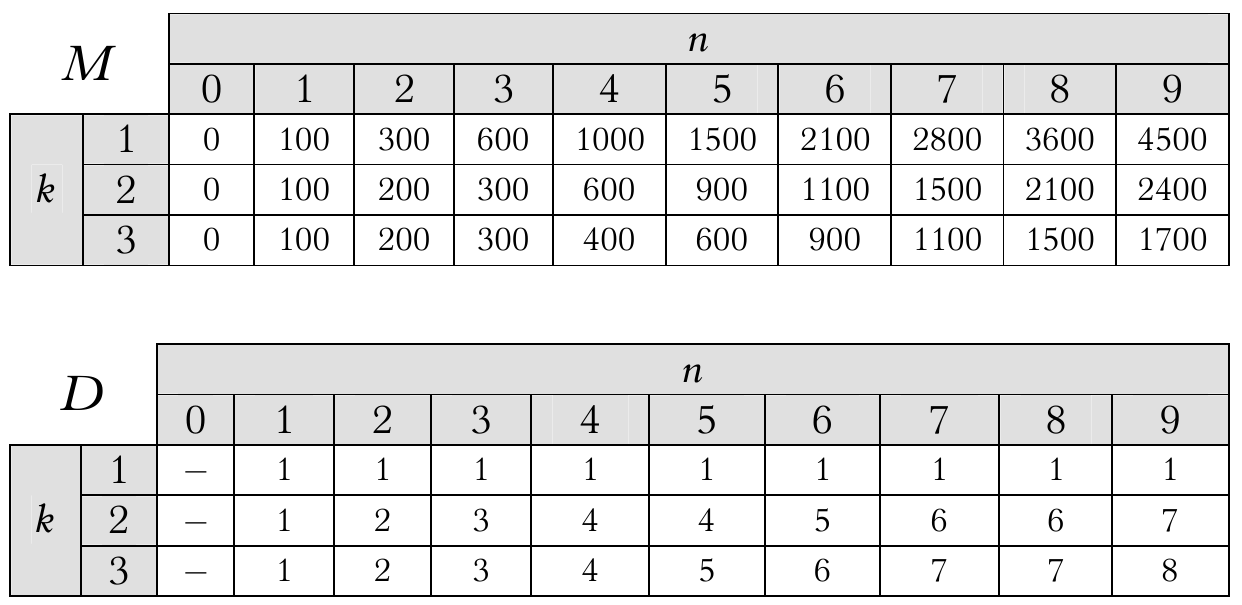
Toliau pateikiame lenteles M ir D, gaunamas jau mūsų nagrinėto pavyzdžio atveju, kai k = 3, n = 9, o puslapių skaičiai pateikti lentelėje:
|
|
|
|
|
|
|
|
|
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
Skaičiuojant langelio ![[k, n]](_images/math/31afbf1a4323bac6b352c91e69095b78e5af172a.png) reikšmę, išbandomos visos
reikšmę, išbandomos visos
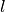 reikšmės nuo 1 iki
reikšmės nuo 1 iki  , masyve
, masyve M įsimenama
mažiausia reiškinio
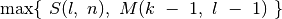 reikšmė ir
pasižymima masyve
reikšmė ir
pasižymima masyve D.
Aptarkime procedūros paskirstyk sudėtingumą. Algoritmas
apskaičiuoja kiekvieną 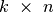 dydžio lentelės
langelį. Kiek gi laiko sugaištama vieno langelio reikšmei
apskaičiuoti? Vidutiniu atveju išbandomų
dydžio lentelės
langelį. Kiek gi laiko sugaištama vieno langelio reikšmei
apskaičiuoti? Vidutiniu atveju išbandomų 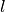 reikšmių
skaičius tiesiškai priklauso nuo
reikšmių
skaičius tiesiškai priklauso nuo  , o su kiekviena
, o su kiekviena 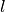 reikšme skaičiuojama funkcijos
reikšme skaičiuojama funkcijos 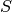 , sumuojančios puslapių
skaičių iš tam tikro intervalo, reikšmė. Pastarosios funkcijos
sudėtingumas taip pat tiesiškai priklauso nuo
, sumuojančios puslapių
skaičių iš tam tikro intervalo, reikšmė. Pastarosios funkcijos
sudėtingumas taip pat tiesiškai priklauso nuo  , t. y. yra
, t. y. yra
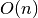 . Taigi:
. Taigi:
vienam langeliui sugaištama
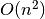 laiko;
laiko;bendras algoritmo sudėtingumas yra
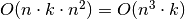 .
.
Nors tai palankus (polinominis) sudėtingumas šiam gana sudėtingam
uždaviniui, jį galima pagerinti efektyviau skaičiuojant funkcijos
S reikšmes. Paprasčiausia būtų apskaičiuoti visas galimas jos
reikšmes iš anksto ir įsiminti masyve, vėliau prireikus S(i, j)
reikšmės, tereiktų jos reikšmę paimti iš masyvo, taigi S
sudėtingumas būtų 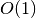 . Visoms reikšmėms apskaičiuoti
prireiktų
. Visoms reikšmėms apskaičiuoti
prireiktų 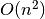 laiko ir tiek pat atminties. Bendro algoritmo
sudėtingumas laiko atžvilgiu būtų
laiko ir tiek pat atminties. Bendro algoritmo
sudėtingumas laiko atžvilgiu būtų
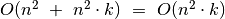 .
.
Tačiau dar efektyvesnis, ir kur kas elegantiškesnis sprendimas yra iš
anksto susiskaičiuoti knygų nuo 1-osios iki 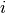 -osios puslapių
sumas visiems
-osios puslapių
sumas visiems 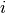 , t. y. tegu
, t. y. tegu
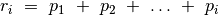 . Jas suskaičiuoti galima
per
. Jas suskaičiuoti galima
per  , pastebėjus, kad
, pastebėjus, kad 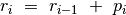 .
Tuomet, jei mus domina knygų nuo
.
Tuomet, jei mus domina knygų nuo 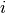 -osios iki
-osios iki 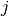 -osios
puslapių suma, ją galima apskaičiuoti per
-osios
puslapių suma, ją galima apskaičiuoti per 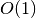 (konstantinį
laiką), atliekant vieną aritmetinę operaciją:
(konstantinį
laiką), atliekant vieną aritmetinę operaciją:
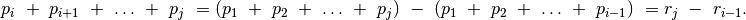
Žemiau pateiksime (pažymėdami specialiu komentaru pakeistas eilutes)
efektyviau realizuotą procedūrą paskirstyk, kurios sudėtingumas
yra 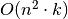 vietoje
vietoje 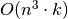 .
.
procedure paskirstyk(k, n : integer;
p : masyvas; { psl. skaičius }
var įvertis : integer;
var nuo : masyvas);
var i, j, l, v : integer; { pagalbiniai kintamieji }
D, M : masyvas2;
r : masyvas; { pagalbinis masyvas}
begin
{ užpildomas masyvas r } // **
r[0] := 0; // **
for j := 1 to n do // **
r[j] := r[j - 1] + p[j]; // **
{ užpildomos kraštinės reikšmės }
for i := 1 to k do
M[i, 0] := 0;
for j := 1 to n do begin
M[1, j] := r[j]; // **
D[1, j] := 1;
end;
{ apskaičiuojama likusi lentelės dalis }
for i := 2 to k do
for j := 1 to n do begin
M[i, j] := BEGALINIS;
{ renkamasis minimumas... }
for l := 1 to j do begin
{ ...iš maksimumų }
v := max(r[j] - r[l - 1], // **
M[i - 1, l - 1]); // **
if v < M[i, j] then begin
M[i, j] := v;
D[i, j] := l;
end;
end;
end;
{ sukonstruojamas optimalus sprendinys }
{ }
...
end;
const int MAXN = ...; // maksimalus knygų skaičius
const int MAXK = ...; // maksimalus darbuotojų skaičius
const int BEGALINIS = ...; // kažkoks kuo didesnis skaičius, pavyzdžiui, 1e9
int k;
int n;
int p; // puslapių skaičius
int ivertis;
int nuo[MAXN+MAXK+1];
void paskristyk () {
int D[MAXK+1][MAXN+1], M[MAXK+1][MAXN+1];
int r[MAXN+MAXK+1]; // pagalbinis masyvas
// užpildomas masyvas r //**
r[0] = 0; //**
for (int j = 1; j <= n; j++) //**
r[j] = r[j-1] + p[j]; //**
// užpildomos kraštinęs reikšmės
for (int i = 1; i <= k; i++)
M[i][0] = 0;
for (int j = 1; j <= n; j++) {
M[1][j] = r[j]; //**
D[1][j] = 1;
}
// apskaičiuojama likusi lentelės dalis
for (int i = 2; i <= k; i++) {
for (int j = 1; j <= n; j++) {
M[i][j] = BEGALINIS;
// renkamas minimumas...
for (int l = 1; l <= j; l++) {
// ...iš maksimumų
v = max(r[j] - r[i-1], M[i-1][l-1]); //**
if (v < M[i][j]) {
M[i][j] = v;
D[i][j] = l;
}
}
}
}
// sukonstruojamas optimalus sprendinys
ivertis = M[k][n];
int j = n;
for (int i = k; i > 1; i--) {
nuo[i] = D[i][j];
j = D[i][j]-1;
/*
jei i-tajam darbuotojui skiriamos knygos nuo D[i][j],
tai likusiems i-1 darbuotojų reikia paskirti
D[i][j]-1 knygų
*/
}
nuo[1] = 1;
}
Uždavinys Sodas 5¶
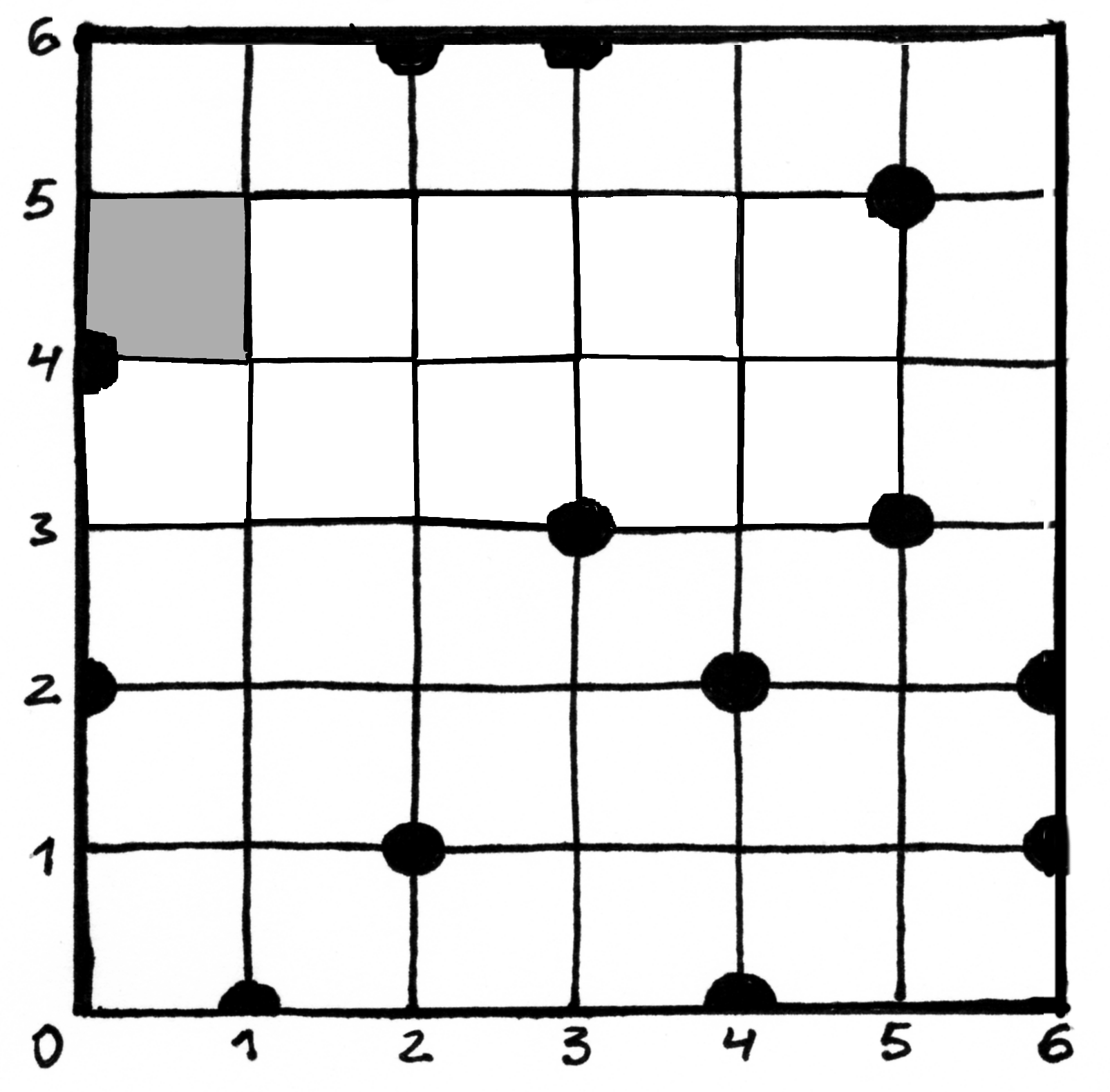
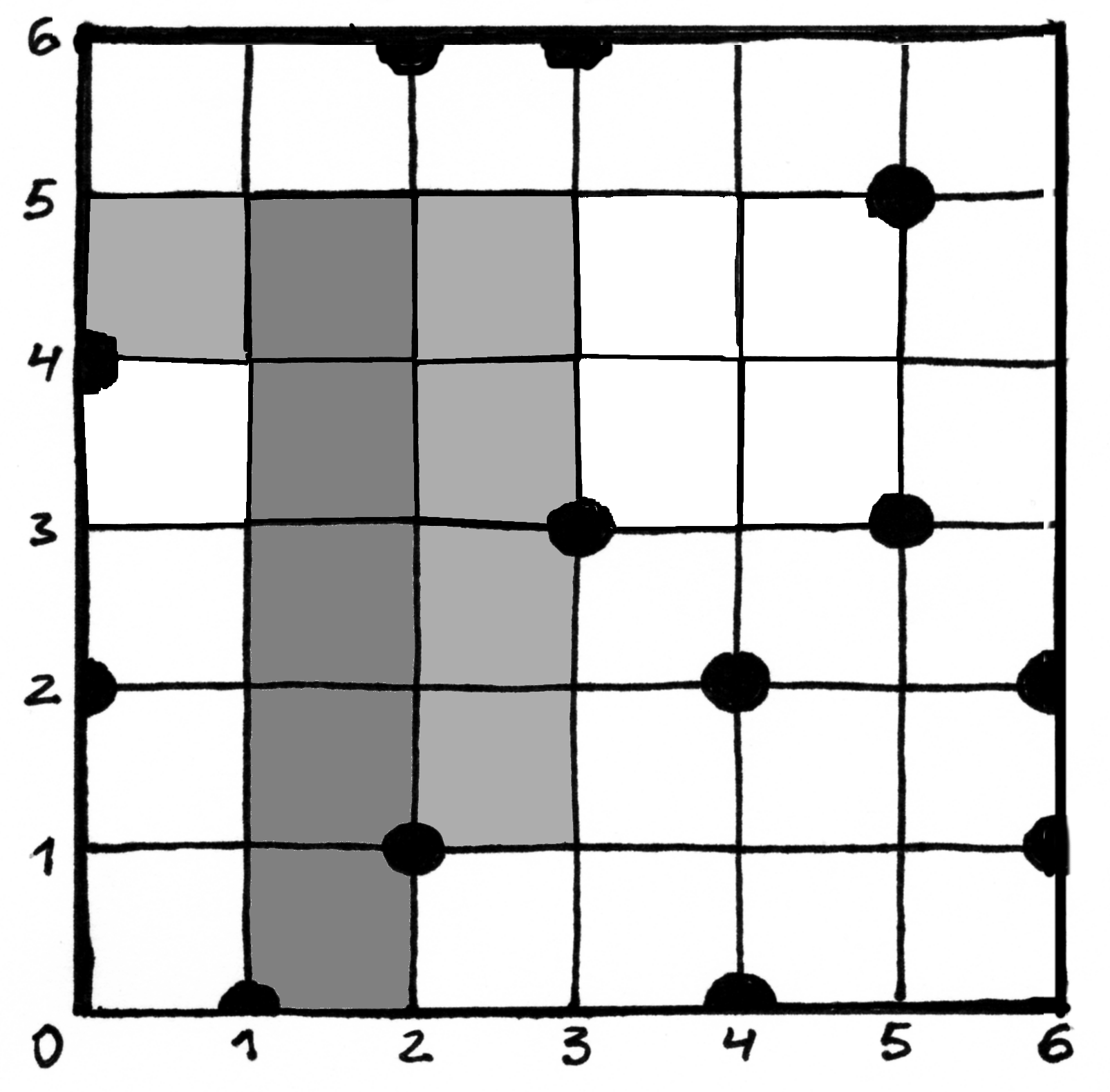
Kvadratiniame
dydžio sode auga
medžių. Laikoma, kad medis yra taškas, neturintis ilgio ir pločio. Koordinačių sistemos pradžia yra apatinis kairysis sodo kampas, o ašys yra lygiagrečios sodo tvoroms. Medžių vietą nusako jų koordinatės
, išreikštos sveikaisiais skaičiais.
Užduotis. Reikia rasti didžiausio stačiakampio, kuriame nebūtų medžių, plotą. Stačiakampio kraštinės turi būti lygiagrečios atitinkamoms sodo tvoroms (kraštinėms).
Ieškomo stačiakampio kraštinėse gali augti medžiai, taip pat stačiakampio kraštinė gali sutapti su sodo tvora.

Fig. 73 Sodo pavyzdys; sode auga trylika medžių¶
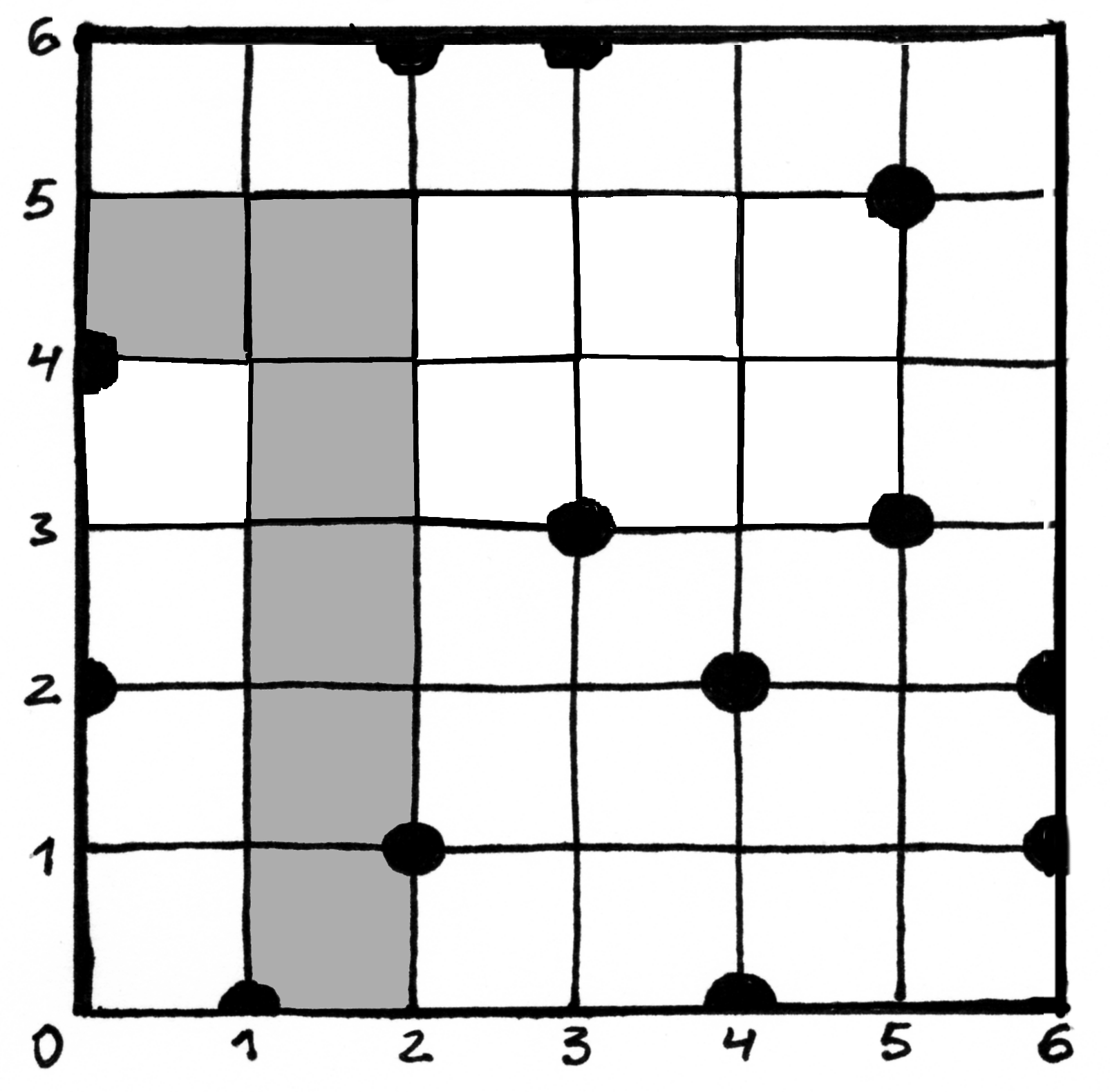
Įveskime keletą sąvokų. 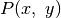 pažymėsime tokį
didžiausią vienetinio pločio stačiakampį, kurio viršutinio
dešiniojo kampo koordinatės yra
pažymėsime tokį
didžiausią vienetinio pločio stačiakampį, kurio viršutinio
dešiniojo kampo koordinatės yra 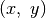 , o kairiosios
kraštinės vidiniuose taškuose nėra medžių. Šio stačiakampio
aukštį žymėsime
, o kairiosios
kraštinės vidiniuose taškuose nėra medžių. Šio stačiakampio
aukštį žymėsime 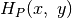 . Nesunku matyti, kaip efektyviai
apskaičiuoti
. Nesunku matyti, kaip efektyviai
apskaičiuoti  reikšmes:
reikšmes:
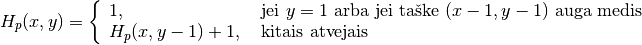
Pažymėkime 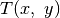 didžiausią medžių neturintį
stačiakampį, kuriam priklauso
didžiausią medžių neturintį
stačiakampį, kuriam priklauso 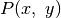 ir kurio aukštis
sutampa su
ir kurio aukštis
sutampa su 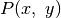 aukščiu.
aukščiu.
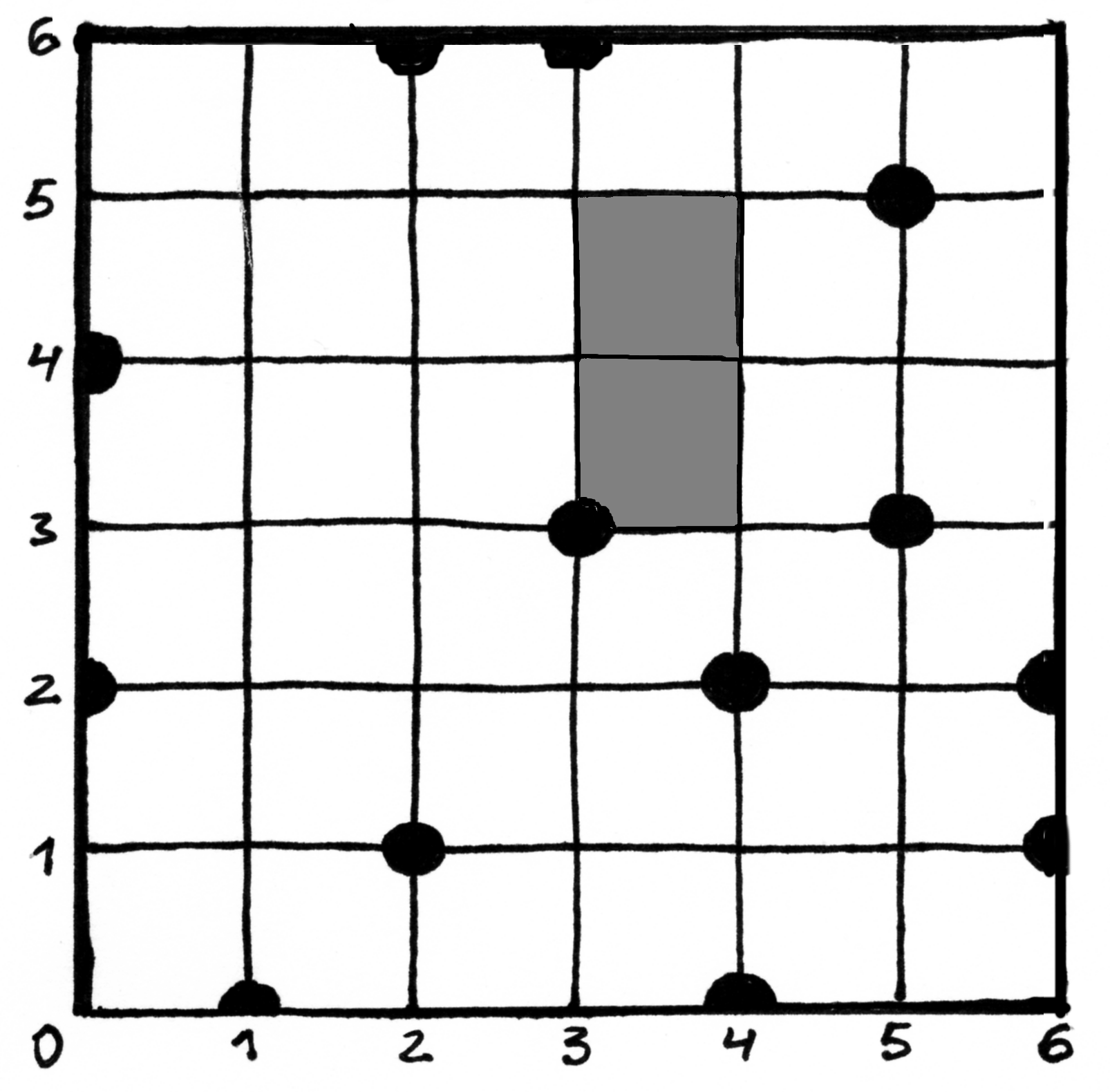
Fig. 74 Stačiakampis 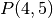 pažymėtas pilkai; jo aukštis
pažymėtas pilkai; jo aukštis
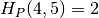 ¶
¶
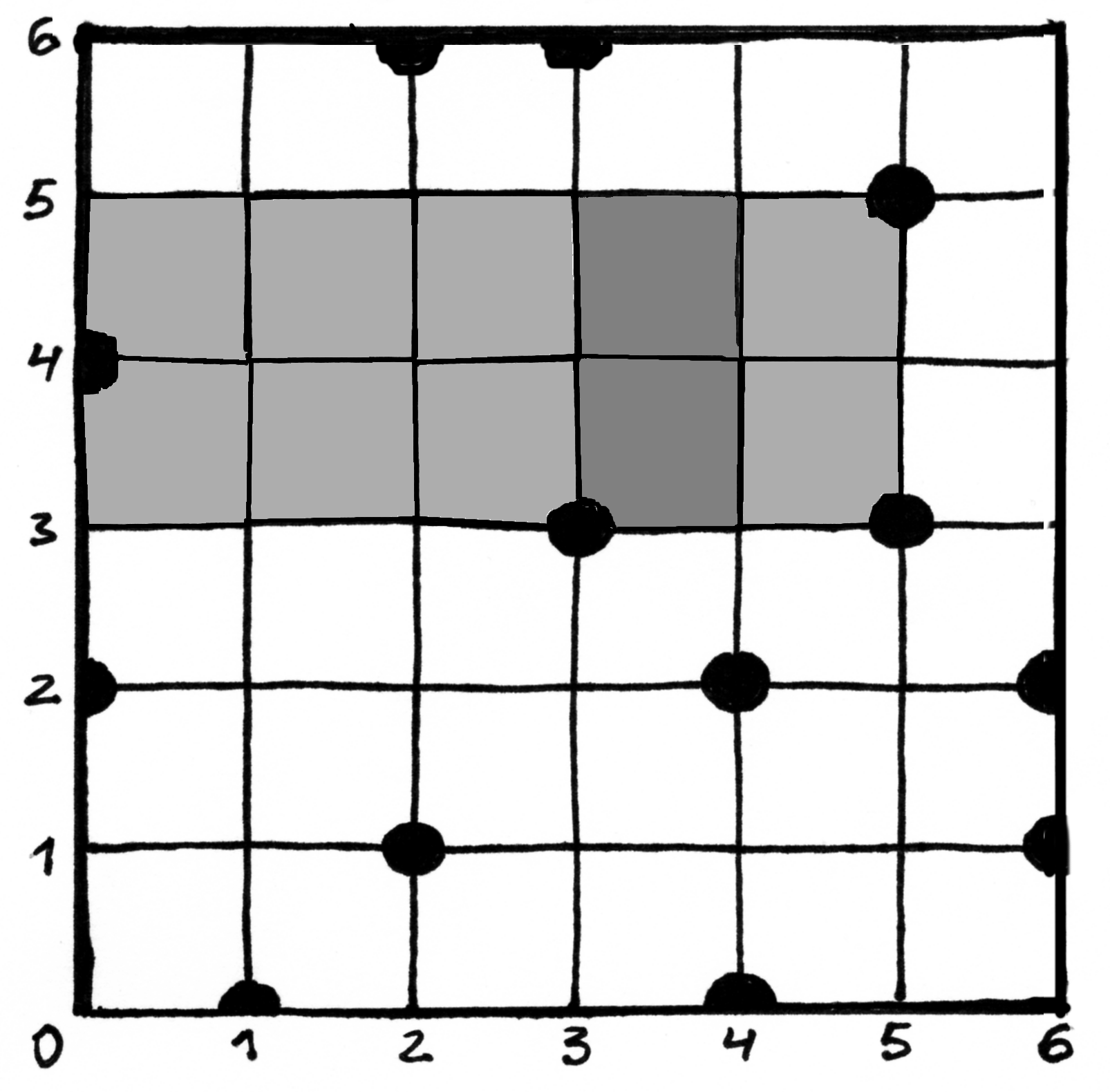
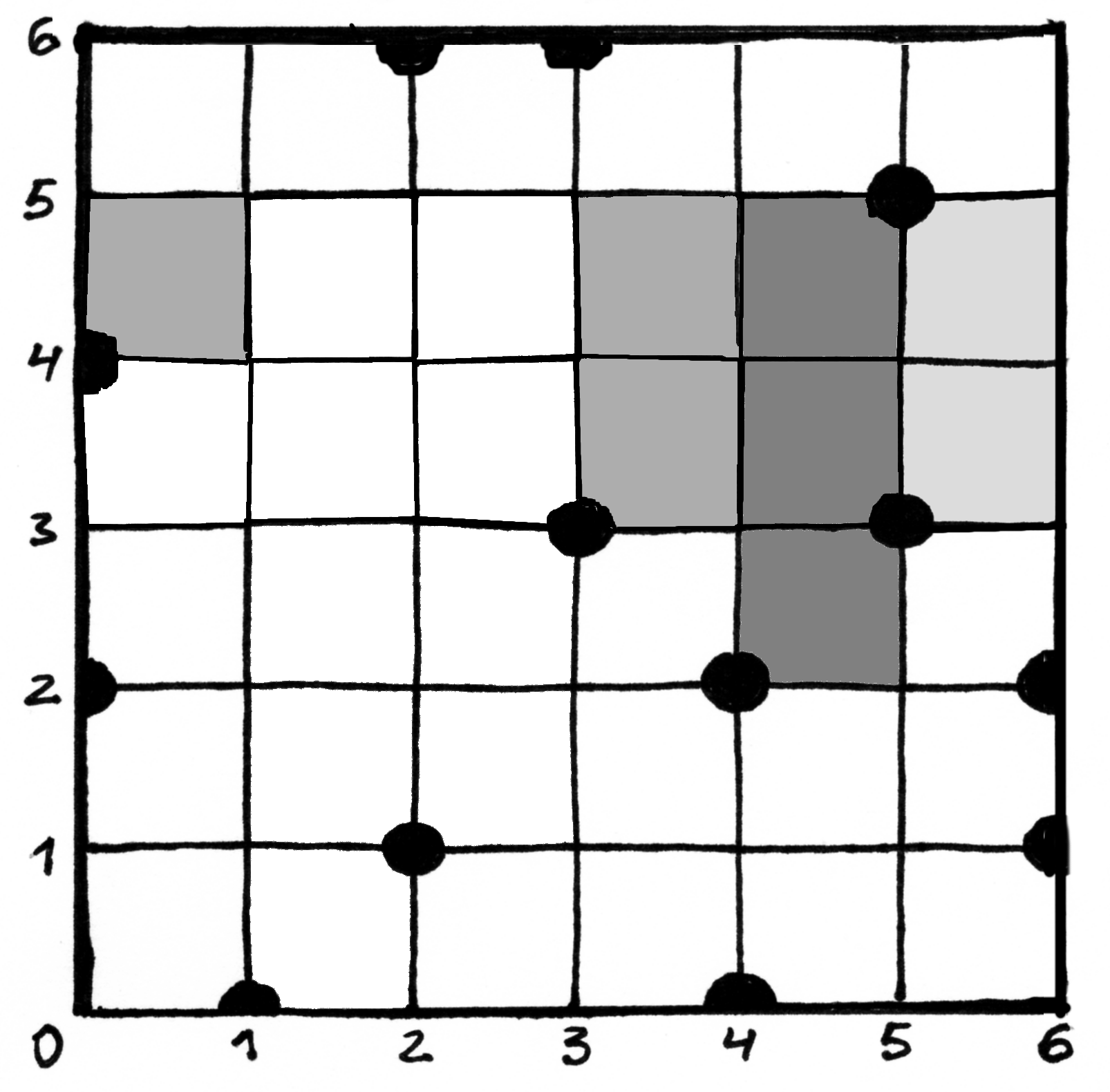
Fig. 75 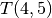 – maksimalaus ploto stačiakampis, kuriam
priklauso
– maksimalaus ploto stačiakampis, kuriam
priklauso 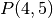 ¶
¶
Stačiakampio 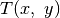 kairiojo viršutiniojo kampo koordinatę
kairiojo viršutiniojo kampo koordinatę
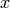 pažymėkime
pažymėkime 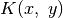 , o dešiniojo viršutinio –
, o dešiniojo viršutinio –
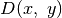 . Žinodami tai, iš karto galėsime apskaičiuoti
. Žinodami tai, iš karto galėsime apskaičiuoti
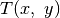 plotą:
plotą:
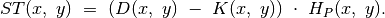
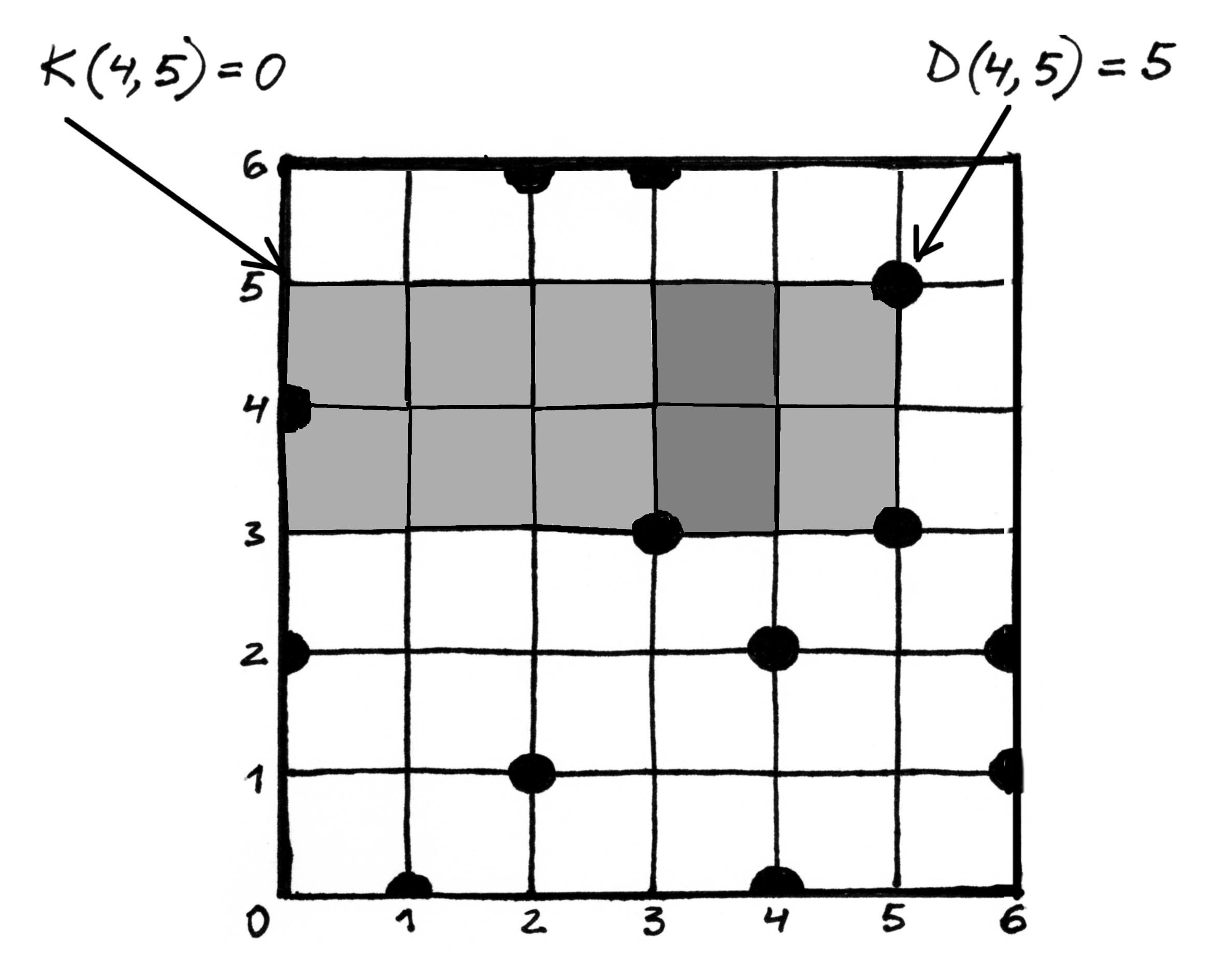
Fig. 76 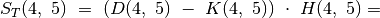
 ¶
¶
Tarkime, kad žinome, kaip efektyviai apskaičiuoti funkcijų 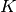 ir
ir 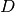 reikšmes. Tuomet užtenka peržiūrėti visus galimus
stačiakampius
reikšmes. Tuomet užtenka peržiūrėti visus galimus
stačiakampius 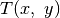 (t. y. išbandyti visas galimas
(t. y. išbandyti visas galimas
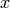 ir
ir 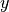 poras, kurių bus
poras, kurių bus 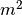 ) ir išrinkti
didžiausią – jis ir bus ieškomasis sprendinys.
) ir išrinkti
didžiausią – jis ir bus ieškomasis sprendinys.
Toliau pateikta procedūra naudoja dvimatį loginį masyvą medis,
kurio kiekvienas elementas medis[x, y] rodo, ar taške
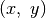 auga medis.
auga medis.
const MAXM = ...; { maksimalus sodo dydis }
type lgmasyvas = array [0..MAXM, 0..MAXM] of boolean;
kvmasyvas = array [1..MAXM, 1..MAXM] of integer;
function max_sodas(m : integer; { sodo dydis }
{ medis[x, y] = true, jei (x, y) auga medis }
var medis : lgmasyvas) : integer;
var x, y, plotas : integer;
Hp, K, D : kvmasyvas;
begin
{ apskaičiuojame Hp reikšmes }
for y := 1 to m do
for x := 1 to m do
if y = 1 then
Hp[x, y] := 1
else if medis[x - 1, y - 1] then
Hp[x, y] := 1
else
Hp[x, y] := Hp[x, y - 1] + 1;
{ apskaičiuojame K ir D reikšmes kiekvienam stačiakampiui T
(šių procedūrų tekstas bus pateiktas vėliau) }
skaičiuok_K(m, Hp, K);
skaičiuok_D(m, Hp, D);
{ belieka peržiūrėti visus stačiakampius ir išrinkti didžiausią }
max_sodas := 0;
for y := 1 to m do
for x := 1 to m do begin
plotas := Hp[x, y] * (D[x, y] - K[x, y]);
if plotas > max_sodas then
max_sodas := plotas;
end;
end;
const int MAXM = ...; // maksimalus sodo dydis
int m; // sodo dydis
bool medis[MAXM+1][MAXM+1]; // medis[x][y] = true, jei (x, y) auga medis
int Hp[MAXM+1][MAXM+1];
int K[MAXM+1][MAXM+1];
int D[MAXM+1][MAXM+1];
int maxSodas () {
// apskaičiuojame Hp reikšmes
for (int y = 1; y <= m; y++) {
for (int x = 1; x <= m; x++) {
if (y == 1)
Hp[x][y] = 1;
else if (medis[x-1][y-1])
Hp[x][y] = 1;
else
Hp[x][y] = Hp[x][y-1] + 1;
}
}
// apskaičiuojame K ir D reikšmes kiekvienam stačiakampiui T
// šių procedūrų tekstas bus pateiktas vėliau
skaiciuokK();
skaiciuokD();
// belieka peržiūrėti visus stačiakampius ir išrinkti didžiausią
int maxPlotas = 0;
for (int y = 1; y <= m; y++) {
for (int x = 1; x <= m; x++) {
int plotas = Hp[x][y] * (D[x][y] - K[x][y]);
if (plotas > maxPlotas)
maxPlotas = plotas;
}
}
return maxPlotas;
}
Pagalvokime, kaip efektyviai apskaičiuoti masyvų K ir D
reikšmes. K ir D reikšmės kiekvienai eilutei (t. y.
kiekvienai koordinatei 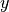 ) bus skaičiuojamos atskirai, tad
panagrinėsime, kaip apskaičiuoti
) bus skaičiuojamos atskirai, tad
panagrinėsime, kaip apskaičiuoti K ir D reikšmes, kai
koordinatė 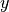 fiksuota.
fiksuota.
Pradėkime nuo masyvo D. Efektyviai reikšmėms apskaičiuoti bus
naudojama dėklo 6 duomenų struktūra. Dėkle saugomos
tos 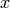 koordinatės, kurioms
koordinatės, kurioms 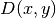 dar neapskaičiuotas.
Koordinatės
dar neapskaičiuotas.
Koordinatės 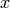 peržiūrimos iš kairės į dešinę (t. y. nuo
1 iki
peržiūrimos iš kairės į dešinę (t. y. nuo
1 iki 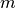 ) ir paeiliui dedamos į dėklą. Tačiau prieš tai
patikrinama, galbūt
) ir paeiliui dedamos į dėklą. Tačiau prieš tai
patikrinama, galbūt 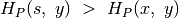 ,
kur
,
kur  – paskutinis dėkle esantis elementas. Jei
– paskutinis dėkle esantis elementas. Jei
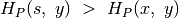 , tai stačiakampio, kuriam priklauso
, tai stačiakampio, kuriam priklauso
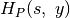 , daugiau į dešinę pratęsti negalima, taigi rastas
dešinysis stačiakampio
, daugiau į dešinę pratęsti negalima, taigi rastas
dešinysis stačiakampio 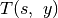 kraštas:
kraštas:
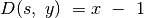 . Tokiu atveju iš dėklo pašalinama
koordinatė
. Tokiu atveju iš dėklo pašalinama
koordinatė  , nes
, nes 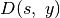 jau apskaičiuota. Jei iš
dėklo pašalinta koordinatė, vėl tikrinama, ar
jau apskaičiuota. Jei iš
dėklo pašalinta koordinatė, vėl tikrinama, ar
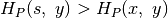 , kur
, kur  – jau atnaujintas
paskutinis dėklo elementas. Galbūt ir šiam elementui bus rastas
– jau atnaujintas
paskutinis dėklo elementas. Galbūt ir šiam elementui bus rastas
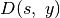 , o pats elementas – pašalintas iš dėklo.
Koordinatė
, o pats elementas – pašalintas iš dėklo.
Koordinatė  į dėklą įtraukiama tik tada, kai
į dėklą įtraukiama tik tada, kai
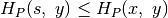 arba kai dėklas jau tuščias.
arba kai dėklas jau tuščias.
Peržiūrėjus visas 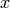 koordinates, dėkle liks tik tos
koordinates, dėkle liks tik tos
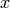 koordinatės, kurių stačiakampio
koordinatės, kurių stačiakampio 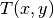 dešinysis
kraštas sutampa su kvadrato kraštu.
dešinysis
kraštas sutampa su kvadrato kraštu.
Pateiktame pavyzdyje parodysime, kaip skaičiuojamos funkcijos 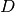 reikšmės, konkrečiu atveju – kai
reikšmės, konkrečiu atveju – kai 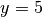 .
.
|
|
|
|
radome
|
|
|
|
radome
|
|
|
|
|
|
radome
|
|
|
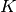 reikšmės skaičiuojamos analogiškai, tik koordinatės
peržiūrimos iš dešinės į kairę.
reikšmės skaičiuojamos analogiškai, tik koordinatės
peržiūrimos iš dešinės į kairę.
type masyvas = array [1..MAXM] of integer;
procedure skaičiuok_D(m : integer;
var Hp : kvmasyvas;
var D : kvmasyvas);
var dėklas : masyvas;
sk, x, y, s : integer;
begin
sk := 0; { Elementų skaičius dėkle }
for y := 1 to m do begin
for x := 1 to m do begin
if sk > 0 then begin
s := dėklas[sk];
while (sk > 0) and
(Hp[x, y] < Hp[s, y]) do
begin
{ rastas dešinysis T(s, y) kraštas (x - 1) }
D[s, y] := x - 1;
sk := sk - 1;
if sk > 0 then s := dėklas[sk];
end;
end;
{ koordinatė x dedama į dėklą }
sk := sk + 1;
dėklas[sk] := x;
end;
{ jei dėkle likus koordinatė x, tai T(x, y) tęsiasi
iki pat dešiniojo sodo krašto }
while sk > 0 do begin
s := dėklas[sk];
D[s, y] := m;
sk := sk - 1;
end;
end;
end;
procedure skaičiuok_K(m : integer;
var Hp : kvmasyvas;
var K : kvmasyvas);
var dėklas : masyvas;
sk, x, y, s : integer;
begin
sk := 0; { Elementų skaičius dėkle }
for y := 1 to m do begin
for x := m downto 1 do begin
if sk > 0 then begin
s := dėklas[sk];
while (sk > 0) and
(Hp[x, y] < Hp[s, y]) do
begin
{ rastas kairysis T(s, y) kraštas (x) }
K[s, y] := x - 1;
sk := sk - 1;
if sk > 0 then s := dėklas[sk];
end;
end;
{ koordinatė x dedama į dėklą }
sk := sk + 1;
dėklas[sk] := x;
end;
{ jei dėkle likus koordinatė x, tai T(x, y) tęsiasi
iki pat kairiojo sodo krašto }
while sk > 0 do begin
s := dėklas[sk];
K[s, y] := 0;
sk := sk - 1;
end;
end;
end;
void skaiciuokD () {
int deklas[MAXM+1];
int sk = 0; // elementų skaičius dėkle
for (int y = 1; y <= m; y++) {
for (int x = 1; x <= m; x++) {
if (sk > 0) {
int s = deklas[sk];
while (sk > 0 && Hp[x][y] < Hp[s][y]) {
// rastas dešinysis T(s, y) kraštas (x-1)
D[s][y] = x-1;
sk--;
if (sk > 0) s = deklas[sk];
}
}
// koordinatė x dedama į dėklą
sk++;
deklas[sk] = x;
}
// jei dėkle likus koordinatė x, tai T(x, y) tęsiasi iki pat dešiniojo sodo krašto
while (sk > 0) {
s = deklas[sk];
D[s][y] = m;
sk--;
}
}
}
void skaiciuokK () {
int deklas[MAXM+1];
int sk = 0; // elementų skaičius dėkle
for (int y = 1; y <= m; y++) {
for (int x = m; x > 0; x--) {
if (sk > 0) {
int s = deklas[sk];
while (sk > 0 && Hp[x][y] < Hp[s][y]) {
// rastas kairysis T(s, y) kraštas (x-1)
K[s][y] = x-1;
sk--;
if (sk > 0) s = deklas[sk];
}
}
// koordinatė x dedama į dėklą
sk++;
deklas[sk] = x;
}
// jei dėkle likus koordinatė x, tai T(x, y) tęsiasi iki pat kairiojo sodo krašto
while (sk > 0) {
s = deklas[sk];
K[s][y] = 0;
sk--;
}
}
}
Šio sprendimo sudėtingumas pagal laiką ir atmintį –
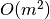 . Nesunkiai galime modifikuoti sprendimą taip, kad
sudėtingumas pagal atmintį sumažėtų iki
. Nesunkiai galime modifikuoti sprendimą taip, kad
sudėtingumas pagal atmintį sumažėtų iki 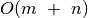 .
Medžių koordinates galima saugoti vienmačiame
.
Medžių koordinates galima saugoti vienmačiame 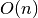 įrašų
masyve, o kvadratą nagrinėti po vieną eilutę: apskaičiuoti
įrašų
masyve, o kvadratą nagrinėti po vieną eilutę: apskaičiuoti
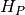 ,
, 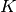 , ir
, ir 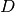 einamajai
einamajai 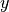 koordinatei,
išrinkti didžiausią iki šiol rastą stačiakampį ir toliau
nagrinėti kitą
koordinatei,
išrinkti didžiausią iki šiol rastą stačiakampį ir toliau
nagrinėti kitą 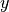 koordinatę. Skaičiuojant
koordinatę. Skaičiuojant 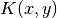 ir
ir
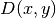 reikšmes,
reikšmes, 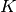 ir
ir 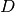 reikšmių su kitomis
reikšmių su kitomis
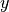 koordinatėmis neprireikia, o skaičiuojant
koordinatėmis neprireikia, o skaičiuojant 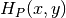 reikšmę naudojamos tik
reikšmę naudojamos tik 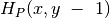 reikšmės.
reikšmės.
Kada taikyti dinaminį programavimą¶
Išsprendėme kelis uždavinius pritaikę dinaminį programavimą. Bendru atveju sunku įvertinti, ar uždavinį galima spręsti taikant dinaminį programavimą. Tačiau dažnai tokie uždaviniai pasižymi bendromis savybėmis. Šiame skyrelyje jas ir apžvelgsime. Prieš taikant dinaminį programavimą reikėtų užduoti šiuos klausimus:
Ar tai optimizavimo uždavinys? Ar šiam uždaviniui galima rasti daug sprendinių, iš kurių mus domina tik vienas (ilgiausias, trumpiausias ar panašiai)? Dauguma dinaminiu programavimų sprendžiamų uždavinių yra būtent optimizavimo uždaviniai.
Ar uždavinyje aprašyto objekto elementai yra surikiuoti? Daugelio objektų elementai yra surikiuoti iš kairės į dešinę (t. y. tarp dviejų objektų įvestas santykis kairiau), arba apibrėžta kokia nors kitokia tvarka. Pavyzdžiui, muziejaus eksponatai (Kuprinės uždavinyje), dovanos (Teisingų dalybų uždavinyje), medžiai 7 (Sodo uždavinyje), simbolių eilutės simboliai, iškiliojo daugiakampio viršūnės, lapai paieškos medyje ir pan. Tikėtina, kad optimizavimo uždavinį, kuriame objektų elementai yra surikiuoti, galima efektyviai išspręsti dinaminio programavimo metodu.
Jei objekto elementai nėra surikiuoti, tikriausiai teks atsisakyti dinaminio programavimo. Mat tokiu atveju uždavinį sprendžiant dinaminio programavimo metodu, laiko bei atminties sąnaudos būtų eksponentinės eilės (tai reiškia, kad sprendimas būtų visiškai neefektyvus).
Ar galima suskaidyti uždavinį į smulkesnius uždavinius, o tuos
į dar smulkesnius, kol pasiekiamos elementarios ribinės situacijos?
Sakykime, uždavinyje aprašytas objektas turi  elementų. Ar,
paėmę mažiau nei
elementų. Ar,
paėmę mažiau nei  elementų, gausime tą patį uždavinį,
tik su mažesniais parametrais? Jei ne – pritaikyti dinaminio
programavimo nepavyks.
elementų, gausime tą patį uždavinį,
tik su mažesniais parametrais? Jei ne – pritaikyti dinaminio
programavimo nepavyks.
Ar smulkesnių uždavinių sprendiniai turi įtakos didesnių
uždavinių sprendimui? Kokia informacija apie sprendinius mažesniems
nei  elementų objektams yra būtina, norint rasti sprendinį
objektui su
elementų objektams yra būtina, norint rasti sprendinį
objektui su  elementų? Ar turėdami sprendinius visiems
mažesniems nei
elementų? Ar turėdami sprendinius visiems
mažesniems nei  elementų objektams bei
elementų objektams bei  -ąjį
elementą galime, gauti sprendinį objektui iš
-ąjį
elementą galime, gauti sprendinį objektui iš  elementų? Jei
ne – dinaminio programavimo pritaikyti taip pat nepavyks.
elementų? Jei
ne – dinaminio programavimo pritaikyti taip pat nepavyks.
Ar skaidant į smulkesnius uždavinius, tie smulkesni uždaviniai ima kartotis? Jei ne – dinaminio programavimo taikyti neverta. Nes dinaminio programavimo efektyvumas laiko atžvilgiu bus toks pat, kaip ir pilno perrinkimo atveju, tačiau pareikalaus kur kas daugiau atminties. Dinaminio programavimo esmę sudaro dalinių uždavinių sprendinių įsiminimas, kai dėl to nebereikia iš naujo nespręsti tų pačių uždavinių. Tačiau jei daliniai uždaviniai 8 nesikartoja, tai nieko nelaimėsime taikydami dinaminį programavimą.
Ar sprendimui pakaks atminties? Taikant dinaminį programavimą dažnai reikia atsižvelgti į atminties sąnaudas. Jos būna kur kas didesnės nei sprendžiant uždavinį, pavyzdžiui, grįžimo metodu. Reikalingas atminties kiekis kartais gali nulemti, ar tam uždaviniui pavyks pritaikyti dinaminį programavimą.
Reikėtų atkreipti dėmesį į spręstų uždavinių sudėtingumą
pagal atmintį. Pavyzdžiui, Kuprinės uždavinio sprendimo
sudėtingumas atminties atžvilgiu yra 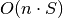 . Jei
eksponatų svoriai būtų dideli, dinaminio programavimo pritaikyti
nepavyktų. Tad pradinių duomenų ribojimai yra labai svarbūs
įvertinant, ar uždavinio sprendimui galima taikyti dinaminį
programavimą.
. Jei
eksponatų svoriai būtų dideli, dinaminio programavimo pritaikyti
nepavyktų. Tad pradinių duomenų ribojimai yra labai svarbūs
įvertinant, ar uždavinio sprendimui galima taikyti dinaminį
programavimą.
Beje, jei ieškoma tik sprendinio vertė, o ne pats sprendinys, dažnai
galima sutaupyti atminties. Pavyzdžiui, Kuprinės uždavinyje užtektų
saugoti ne visą lentelę, o tik dvi einamąsias lentelės eilutes,
kadangi skaičiuojant  -osios lentelės eilutės reikšmes
naudojamos tik reikšmės iš
-osios lentelės eilutės reikšmes
naudojamos tik reikšmės iš 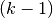 -osios eilutės.
-osios eilutės.
Išnašos
- 1
Jei reikalinga tik optimalaus sprendinio vertė, tai galima sudaryti efektyvesnį atminties atžvilgiu algoritmą. Pavyzdžiui, skaičiuojant Fibonačio skaičius iš apačios į viršų, nereikia saugoti atmintyje viso masyvo – pakanka įsiminti du paskutinius suskaičiuotus narius.
- 2
Panašus uždavinys buvo pateiktas Vidurio Europos informatikos olimpiadoje, kuri vyko Vengrijoje 1995 m.
- 3
Simbolis „
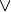 “ reiškia loginę operaciją „arba“;
Paskalio kalboje tai atitiktų loginę operaciją
“ reiškia loginę operaciją „arba“;
Paskalio kalboje tai atitiktų loginę operaciją or.- 4
Analogiškas uždavinys pateiktas S. Skienos knygoje The Algorithm Design Manual [S98].
- 5
Panašus uždavinys buvo pateiktas Vidurio Europos informatikos olimpiadoje 1995 metais
- 6
Dėklo duomenų struktūra aprašyta skyrelyje Rekursyvios funkcijos.
- 7
Sodo uždavinyje medis
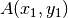 yra kairiau nei medis
yra kairiau nei medis
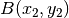 , jei
, jei 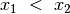 arba
arba 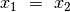 ir
ir 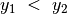 .
.- 8
Yra tokia uždavinio sprendimo strategija Skaldyk ir valdyk, kai uždavinys padalijamas į mažesnius uždavinius, visi mažesni uždaviniai išsprendžiami taikant rekursiją ir sujungus gautus sprendinius gaunamas pradinio uždavinio sprendinys; tik šiuo atveju mažesni uždaviniai nesikartoja ir tarpusavyje neturi nieko bendra; Greitojo rikiavimo algoritmas yra tokios strategijos pavyzdys: rikiuojama seka dalijama į dvi dalis ir kiekviena dalis rikiuojama atskirai, tačiau vienos sekos dalies rikiavimas neturi įtakos kitos dalies rikiavimui.
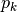
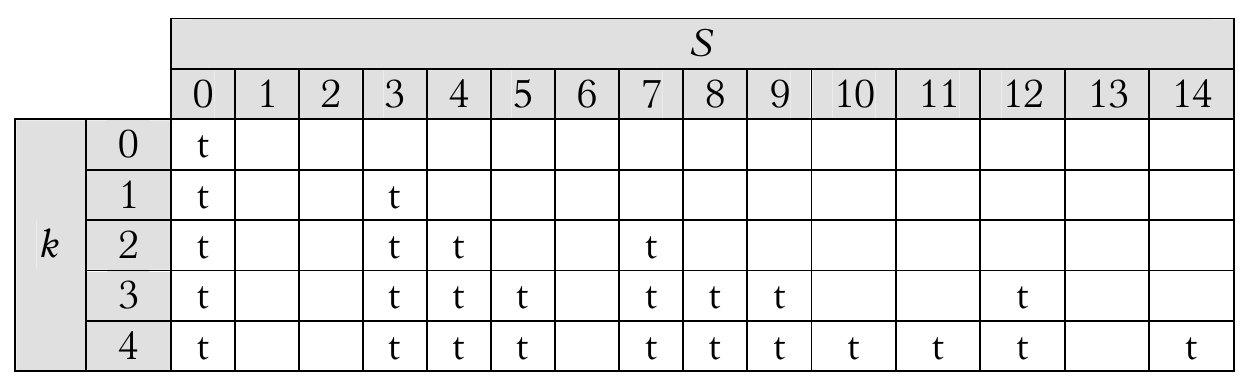
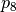
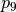
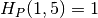 ;
;
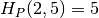 ;
;
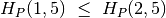 ;
;
 ;
;
 ;
; ;
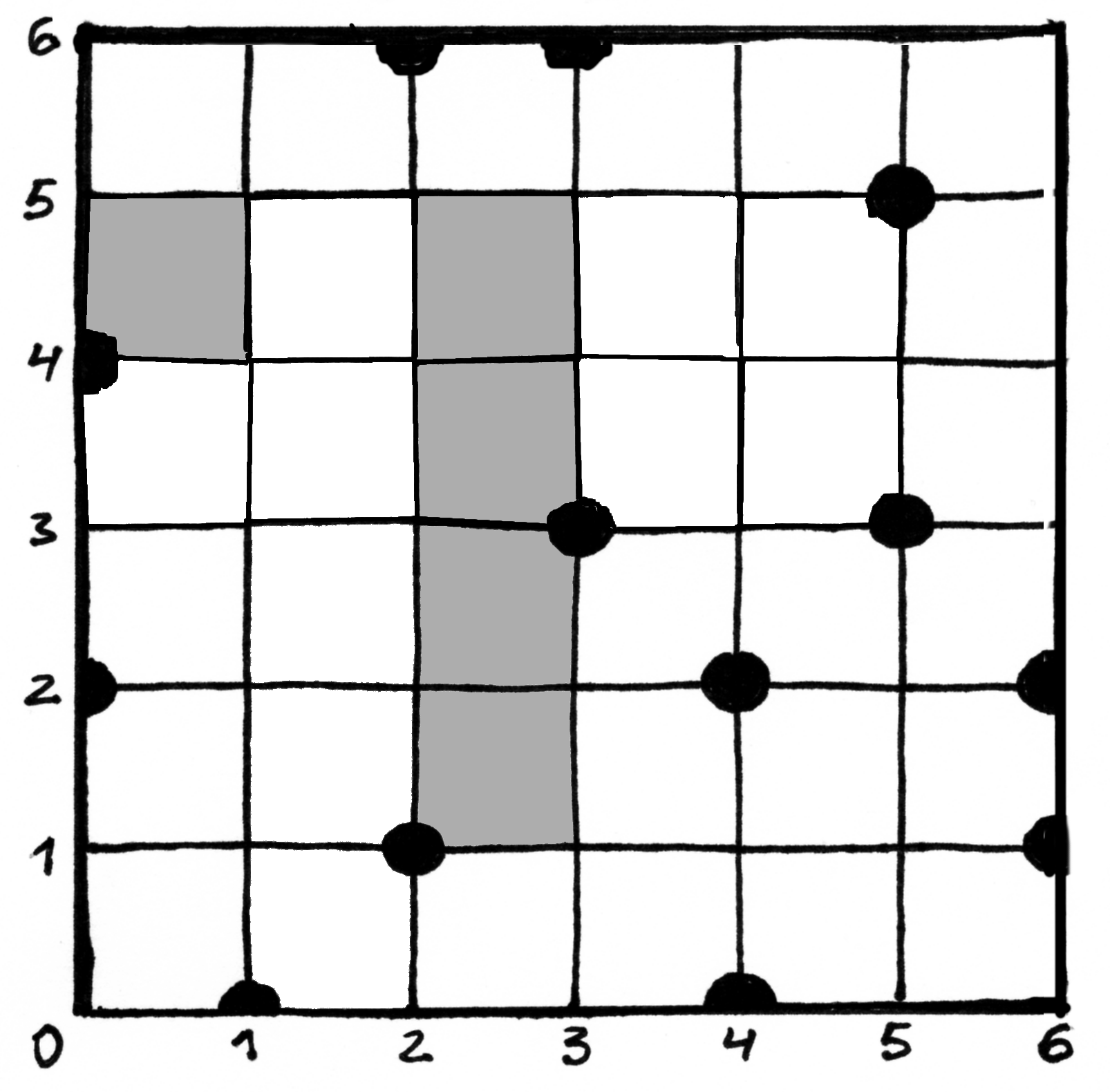
;
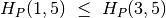 ;
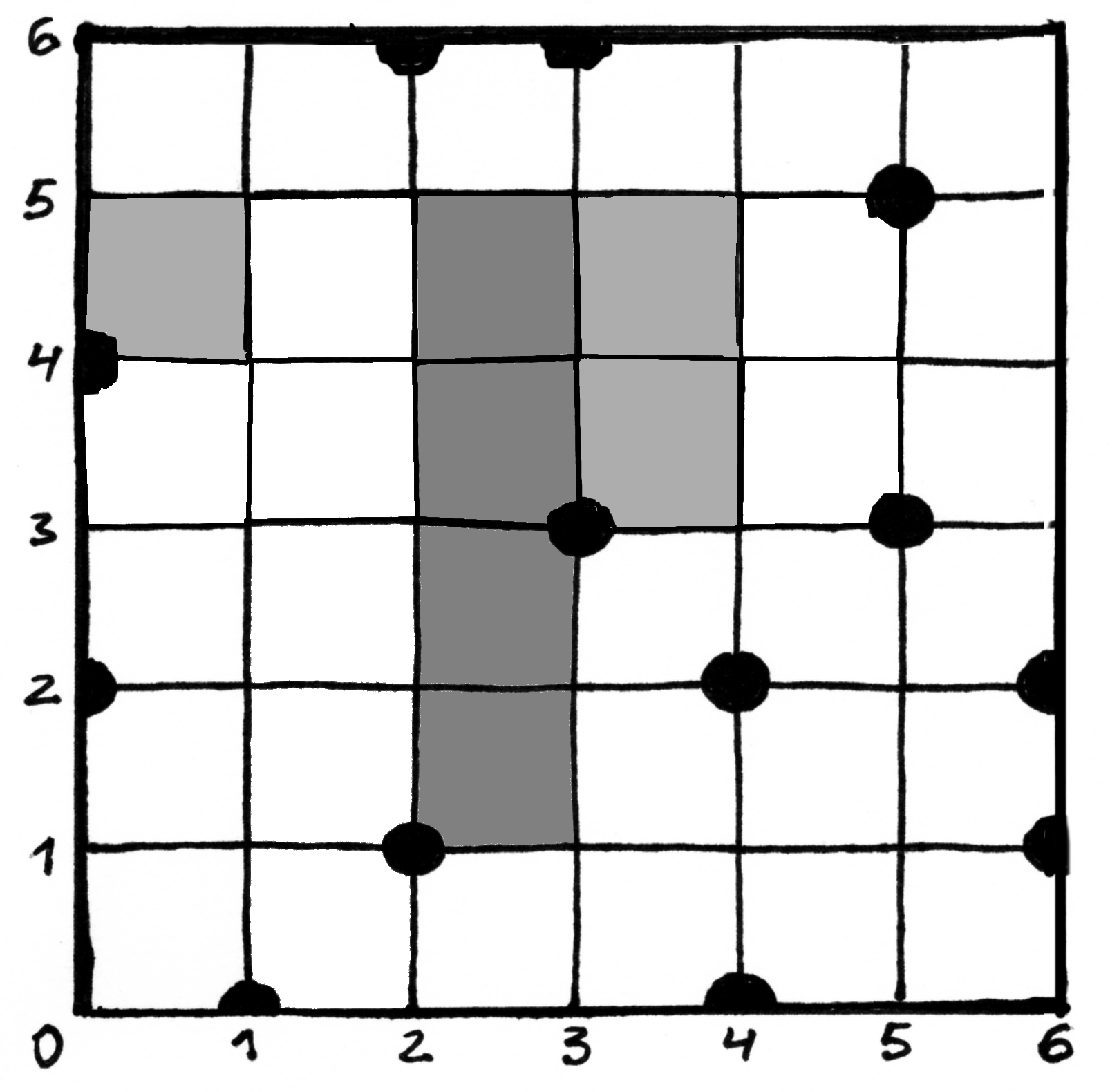
;
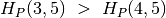 ;
;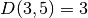 ;
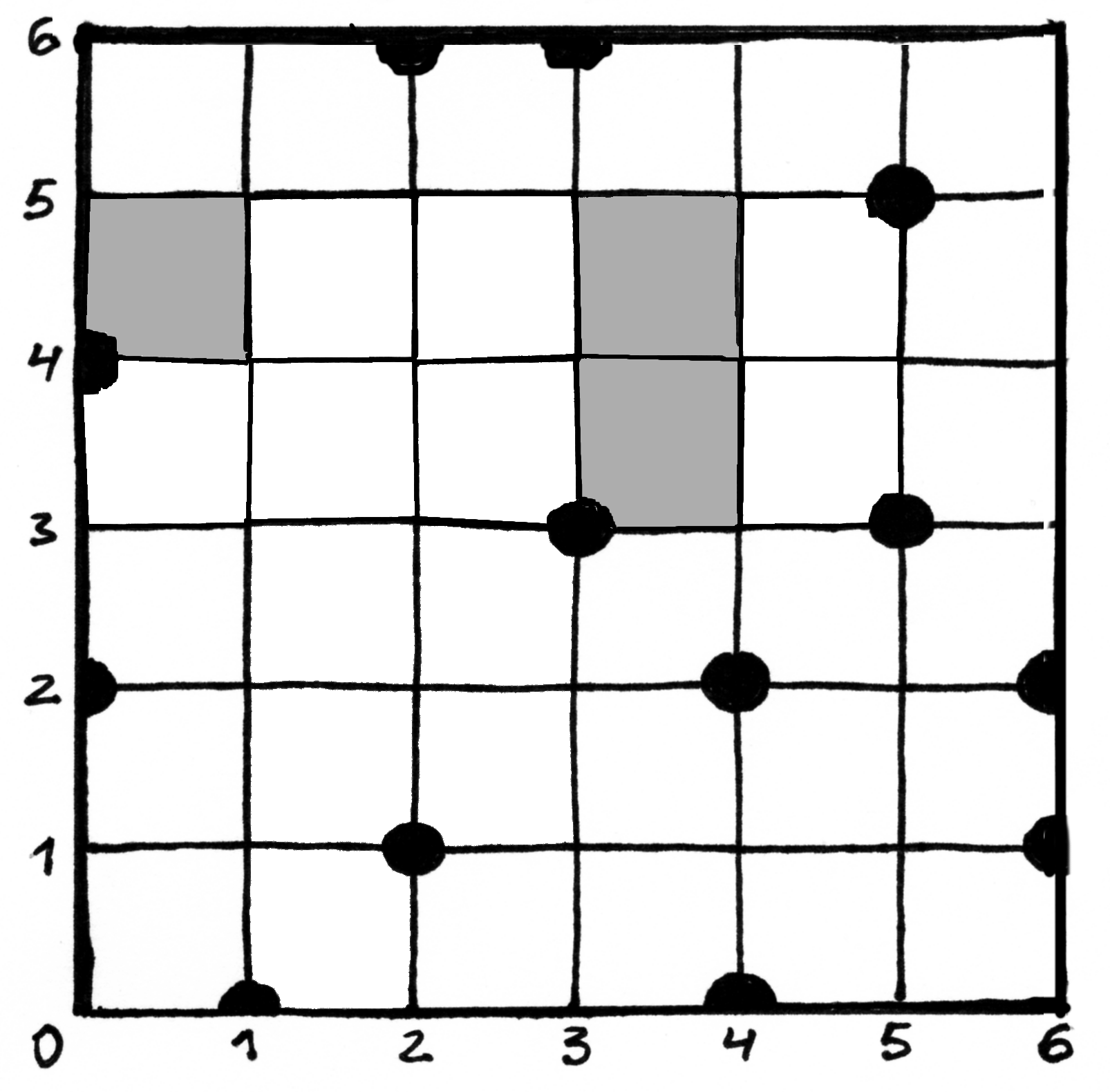
;
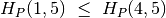 ;
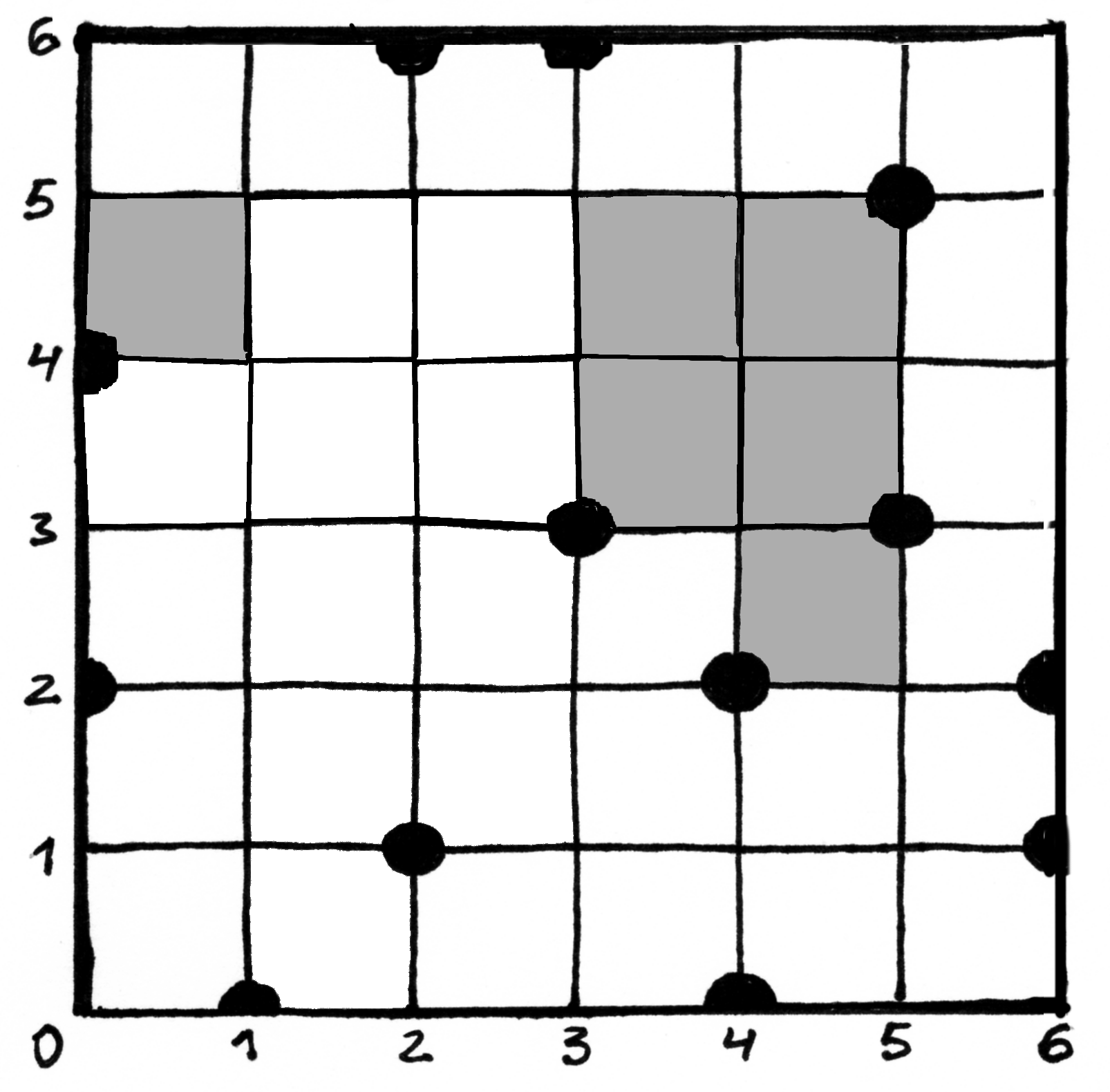
;
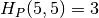 ;
;
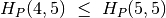 ;
;
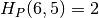 ;
;
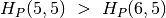 ;
;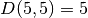 ;
;