Rekursija¶
In order to understand recursion, one must first understand recursion.Norint suprasti rekursiją, pirma reikia suprasti rekursiją.Populiarus humoristinis posakis
Šis humoristinis posakis gana gerai nusako rekursijos esmę: algoritmas yra rekursyvus, jei bent vienas iš jo žingsnių yra to paties algoritmo atlikimas su kitais (dažniausiai mažesniais) duomenimis.
Pažintį su rekursija pradėkime nuo geometrinės figūros, vadinamos Mengerio kempine 1 (ji yra fraktalinis 2 kūnas), konstravimo algoritmo:
žingsnis Paimamas kubas.
žingsnis Kubas suskaidomas į 27 vienodo dydžio kubelius.
žingsnis Pašalinamas kubo viduryje esantis kubelis, taip pat dar 6 kiekvienos sienos viduryje esantys kubeliai.
žingsnis Toliau su kiekvienu likusiu kubeliu veiksmai kartojami nuo antro žingsnio.
Pateiktas konstravimo algoritmas yra rekursyvus, nes ketvirtame žingsnyje nurodoma tą patį algoritmą taikyti kitiems duomenims.
.jpg)
Fig. 8 Mengerio kempinė¶
Rekursyvios funkcijos¶

Fig. 9 Lėkščių krovimas į stirtą primena dėklą — paskutinė padėta lėkštė bus paimta pirmoji¶
Aukšto lygio programavimo kalbos suteikia galimybę aprašyti rekursyvias funkcijas, t. y. funkcijas, kurios iškviečia pačios save. Kiekvieną kartą kreipiantis į funkciją, įsimenamas grįžimo adresas, padaromos parametrų kopijos ir sukuriami nauji lokalūs funkcijos kintamieji.
Tai organizuojama dėklo (angl. stack) duomenų struktūra. Ši struktūra veikia LIFO (angl. Last in First out) principu: nauji duomenys dedami į dėklo „viršų“ ir imami nuo „viršaus“, t. y. imant duomenis visada paimamas paskutinis padėtas duomuo. Taigi kiekvieną rekursyvų algoritmą galima realizuoti nenaudojant rekursijos, o suprogramuojant ir panaudojant savo dėklo duomenų struktūrą.
Rekursyvi funkcija su ją iškvietusia funkcija (savo pačios „kopija“) gali bendrauti tik parametrais bei globaliais kintamaisiais.
Panagrinėkime keletą paprastų rekursyvių funkcijų. Vieną, beje, jau matėme – Euklido algoritmas DBD rasti gali būti užrašomas rekursyviai.
Kitas pavyzdys – skaičiaus faktorialas:
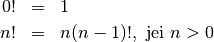
Galime parašyti skaičiaus faktorialą skaičiuojančią funkciją:
function fakt(n : integer) : longint;
begin
if n = 0 then
fakt := 1
else
fakt := n * fakt(n - 1);
end;
long long fakt(int n) {
if(n == 0) return 1;
return n*fakt(n-1);
}
Kreipinio fakt(4) vykdymą iliustruoja žemiau pateiktas paveikslas:

Atlikus kreipinį fakt(n), iš viso bus įvykdyta 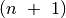 funkcijų kvietimų, taigi šios funkcijos sudėtingumas yra
funkcijų kvietimų, taigi šios funkcijos sudėtingumas yra
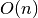 . Šis būdas yra lėtesnis už faktorialo skaičiavimą
ciklu, kadangi funkcijos iškvietimas yra kur kas sudėtingesnis
procesas už ciklo iteraciją.
. Šis būdas yra lėtesnis už faktorialo skaičiavimą
ciklu, kadangi funkcijos iškvietimas yra kur kas sudėtingesnis
procesas už ciklo iteraciją.
Kitas rekursyvios funkcijos pavyzdys – Fibonačio skaičiai. 1202
metais italų matematikas Leonardo Pisano, vadinamas Fibonačiu
(Fibonacci), sugalvojo uždavinį: triušių pora kas mėnesį
atsiveda po du triušiukus (patinėlį ir patelę), o iš atvestųjų
triušiukų po dviejų mėnesių jau gaunamas naujas prieauglis. Kiek
triušių bus po metų, jei metų pradžioje buvo viena jauniklių pora?
Triušių skaičių kiekvieną mėnesį nusakys seka
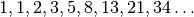 , o šie skaičiai yra vadinami
Fibonačio skaičiais. Juos taip pat galima skaičiuoti rekursyviai:
, o šie skaičiai yra vadinami
Fibonačio skaičiais. Juos taip pat galima skaičiuoti rekursyviai:
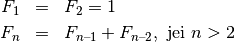
function F(n : integer) : longint;
begin
if n <= 2 then
F := 1
else
F := F(n - 1) + F(n - 2);
end;
long long F(int n) {
if(n <= 2) return 1;
return F(n-1) + F(n-2);
}
Nors ši funkcija atrodo tokia pat paprasta, kaip ir faktorialo, jos
sudėtingumas yra eksponentinis 3. Taip yra todėl, kad kiekviena
funkcija iškviečia net dvi kitas, antrines funkcijas, o joms
perduodami argumentai sumažinami tik pastoviu dydžiu. Iškvietus
F(45), atsakymo tektų palaukti.
Pastebėkime, kad visi minėti uždaviniai pasižymi viena bendra
savybe: spręsdami uždavinį, turime išspręsti analogiškus, bet
mažesnius uždavinius. Pavyzdžiui, jei norime suskaičiuoti
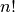 , turime išspręsti mažesnį uždavinį – suskaičiuoti
, turime išspręsti mažesnį uždavinį – suskaičiuoti
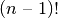 , o jei norime rasti
, o jei norime rasti DBD(25, 15) (pagal Euklido
algoritmą), turime rasti DBD(15, 10).
Hanojaus bokštų uždavinys¶
Išspręsime klasikinį Hanojaus bokštų uždavinį, kurį 1883 metais suformulavo prancūzų matematikas Eduardas Lukas (Edouard Lucas).
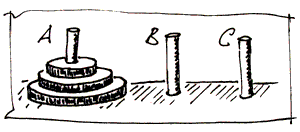
Fig. 10 Pavyzdys su trimis diskais¶
Duoti trys stiebai ir aštuoni skirtingo dydžio diskai. Iš pradžių visi šie diskai sumauti ant pirmojo stiebo: apačioje pats didžiausias diskas, ant jo – mažesnis ir t. t. Viršuje užmautas pats mažiausias iš diskų.
Užduotis. reikia perkelti visus diskus nuo pirmojo stiebo ant paskutinio laikantis šių taisyklių:
Vienu ėjimu galima kelti tik vieną diską.
Diską galima užmauti tik ant tuščio stiebo arba uždėti ant didesnio už jį disko.
Atliekamų perkėlimų skaičius turi būti minimalus.
Praplėsime standartinę uždavinio formuluotę: vietoj aštuonių
diskų reikia perkelti  diskų. Stiebai pavadinti raidėmis A,
B ir C. Parašykite programą, kuri atspausdintų, kaip perkelti visus
diskus, laikantis minėtų taisyklių.
diskų. Stiebai pavadinti raidėmis A,
B ir C. Parašykite programą, kuri atspausdintų, kaip perkelti visus
diskus, laikantis minėtų taisyklių.
Panagrinėkime paprasčiausius atvejus 4. Kai 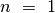 ,
diską perkeliame (ir uždavinį išsprendžiame) vienu žingsniu.
Nesunku jį išspręsti, kai
,
diską perkeliame (ir uždavinį išsprendžiame) vienu žingsniu.
Nesunku jį išspręsti, kai 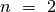 , tam reikia trijų
perkėlimų. Šiek tiek pagalvoję suvokiame, kad pakanka 7 perkėlimų
uždaviniui išspręsti, kai
, tam reikia trijų
perkėlimų. Šiek tiek pagalvoję suvokiame, kad pakanka 7 perkėlimų
uždaviniui išspręsti, kai 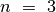 .
.
Atkreipkite dėmesį, kad niekas nepasikeistų, jei uždavinyje būtų reikalaujama diskus perkelti ne ant dešiniojo, o ant vidurinio disko: atliktume tuos pačius ėjimus, tik diskus keltume ne ant dešiniojo, o ant vidurinio ir atvirkščiai.
Ko gi reikia, kad galėtume pagal taisykles perkelti  -ąjį
(patį didžiausią) diską? Visų pirma, ant jo neturi būti jokių
kitų diskų. Be to, dešinysis stiebas taip pat turi būti tuščias.
Vadinasi, visi likę diskai turi būti jau perkelti ant vidurinio
stiebo! Tik tuomet galėsime perkelti
-ąjį
(patį didžiausią) diską? Visų pirma, ant jo neturi būti jokių
kitų diskų. Be to, dešinysis stiebas taip pat turi būti tuščias.
Vadinasi, visi likę diskai turi būti jau perkelti ant vidurinio
stiebo! Tik tuomet galėsime perkelti  -ąjį (didžiausią)
diską.
-ąjį (didžiausią)
diską.
Bandydami 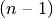 mažesnių diskų perkelti ant vidurinio
stiebo, galime visiškai nekreipti dėmesio į
mažesnių diskų perkelti ant vidurinio
stiebo, galime visiškai nekreipti dėmesio į  -ąjį diską:
jis nesutrukdys, kadangi yra didesnis už visus likusius diskus. Taigi
-ąjį diską:
jis nesutrukdys, kadangi yra didesnis už visus likusius diskus. Taigi
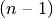 diskų perkėlimas yra visiškai tas pats, tik
sumažintas, uždavinys. Taip pradedame įžvelgti rekursyvų uždavinio
sprendimą, kurio bendra schema tokia:
diskų perkėlimas yra visiškai tas pats, tik
sumažintas, uždavinys. Taip pradedame įžvelgti rekursyvų uždavinio
sprendimą, kurio bendra schema tokia:
Jei norime perkelti n > 0 diskų:
Visus mažesnius diskus perkeliame ant tarpinio stiebo.
Perkeliame
-ąjį diską.
Visus mažesnius diskus perkeliame ant galinio stiebo.
Tegul kelk yra diskų perkėlinėjimo funkcija. Ji turi priklausyti nuo
diskų, kuriuos reikia perkelti, skaičiaus. Be to, ji turi žinoti, nuo
kurio ir ant kurio stiebo norima perkelti diskus. Tai nebus visada tie
patys stiebai A ir C. Pavyzdžiui, jei norėsime  diskų
perkelti nuo stiebo A ant stiebo C, turime
diskų
perkelti nuo stiebo A ant stiebo C, turime 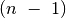 diską
perkelti nuo stiebo A ant stiebo B (ta pati užduotis, tik kitas diskų
skaičius ir stiebų vardai), o vėliau – nuo B ant C. Kintamuosius
žymėsime
diską
perkelti nuo stiebo A ant stiebo B (ta pati užduotis, tik kitas diskų
skaičius ir stiebų vardai), o vėliau – nuo B ant C. Kintamuosius
žymėsime nuo, ant ir tarp (tarpiniam stiebui). Jei
 , diskus perkeliame remdamiesi aukščiau aprašyta
taisykle, o jei
, diskus perkeliame remdamiesi aukščiau aprašyta
taisykle, o jei 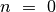 , nereikia atlikti nieko – rekursija
baigiama.
, nereikia atlikti nieko – rekursija
baigiama.
procedure kelk(n : integer; nuo, tarp, ant : char);
begin
if n > 0 then begin
kelk(n - 1, nuo, ant, tarp); { nuo → tarp }
{ perkeliamas n-tasis diskas }
writeln(nuo, ' –> ', ant);
kelk(n - 1, tarp, nuo, ant) { tarp → ant }
end
end;
void kelk(int n, char nuo, char tarp, char ant) {
if(n == 0) return;
kelk(n-1, nuo, ant, tarp); //nuo -> tarp
cout << nuo << " -> " << ant << endl;
kelk(n-1, tarp, nuo, ant); // tarp -> ant
}
Jei norime perkelti  diskų nuo stiebo A ant stiebo C,
iškviečiame
diskų nuo stiebo A ant stiebo C,
iškviečiame kelk(n, 'A', 'B', 'C'). Žemiau iliustruojamas
procedūros veikimas, iškvietus kelk(3, 'A', 'B', 'C'):
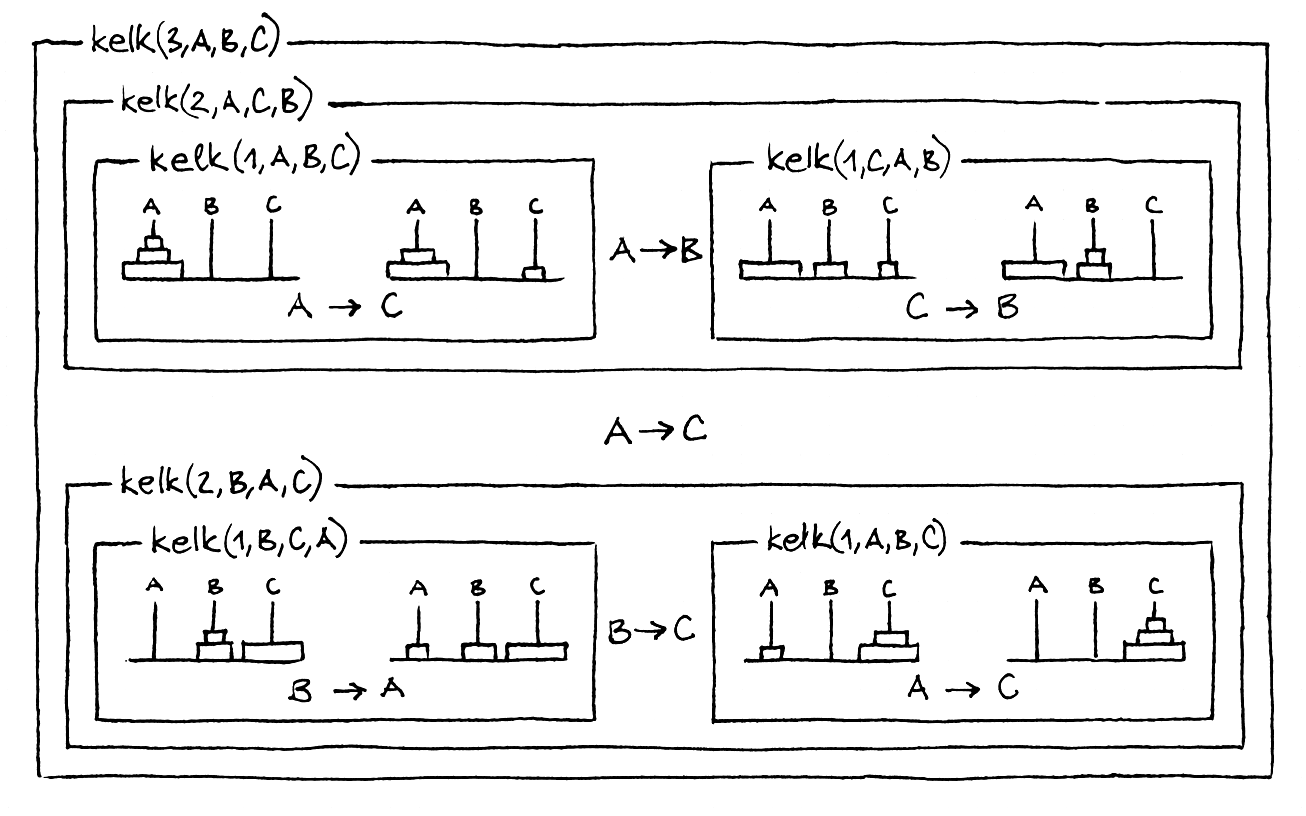
Taigi procedūra atspausdins:
A –> CA –> BC –> BA –> CB –> AB –> CA –> C
Nuostabu, kad šiam, iš pirmo žvilgsnio sudėtingam, uždaviniui egzistuoja toks elegantiškas sprendimas.
Parodysime, jog aprašytuoju būdu kilnojant diskus perkėlimų
skaičius yra mažiausias. Pažymėkime 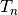 mažiausią
perkėlimų skaičių, reikalingą perkelti
mažiausią
perkėlimų skaičių, reikalingą perkelti  diskų nuo vieno
stiebo ant kito. Žinome, kad
diskų nuo vieno
stiebo ant kito. Žinome, kad 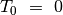 ,
, 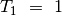 ,
,
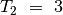 ir
ir 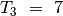 .
.
Be to, iš ankstesnių samprotavimų seka, kad  diskų galima
perkelti
diskų galima
perkelti 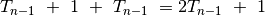 perkėlimais, t. y.:
perkėlimais, t. y.:
(1)¶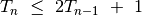
Kita vertus, ar galime ką nors atlikti geriau? Anksčiau ar vėliau
būtinai teks perkelti  -tąjį (didžiausią) diską. Prieš
tai likusieji
-tąjį (didžiausią) diską. Prieš
tai likusieji 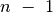 diskų privalės atsidurti ant vidurinio
stiebo, o tam reikės bent
diskų privalės atsidurti ant vidurinio
stiebo, o tam reikės bent 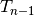 (minimalaus skaičiaus)
perkėlimų. Vieno perkėlimo reikės
(minimalaus skaičiaus)
perkėlimų. Vieno perkėlimo reikės  -ajam diskui, ir pagaliau
dar bent
-ajam diskui, ir pagaliau
dar bent 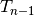 perkėlimų mažesniems diskams perkelti ant
viršaus. Todėl:
perkėlimų mažesniems diskams perkelti ant
viršaus. Todėl:
(2)¶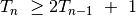
Iš (1) ir (2) nelygybių
gauname, kad 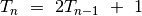 .
.
Taigi 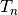 galime apskaičiuoti pagal rekurentinį sąryšį:
galime apskaičiuoti pagal rekurentinį sąryšį:
(3)¶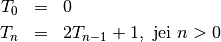
Pavyzdžiui, 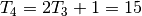 .
.
Tačiau rekurentinis sąryšis neatsako į klausimą, koks procedūros kelk sudėtingumas. Matyti, kad, diskų skaičių padidinus vienetu, ėjimų skaičius maždaug padvigubėja. Norėdami būti tikri, išspręsime rekurentinį sąryšį.
Pažymėkime 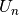 skaičių, vienetu didesnį už
skaičių, vienetu didesnį už 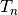 :
t. y.
:
t. y. 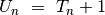 .
.
Pridėję prie (3) lygybių po vienetą, gauname:
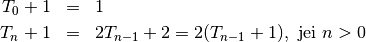
Taigi:
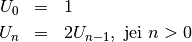
Iš čia matyti, kad
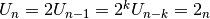 , vadinasi,
, vadinasi,
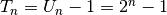 .
.
Procedūros kelk, perkeliančios  diskų, atliekamų
žingsnių skaičius proporcingas
diskų, atliekamų
žingsnių skaičius proporcingas 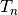 , taigi šios procedūros
sudėtingumas yra
, taigi šios procedūros
sudėtingumas yra 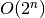 . Palyginkime procedūrą
. Palyginkime procedūrą kelk su
Fibonačio skaičių skaičiavimo funkcija 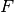 – kiekviena jų
atlieka du rekursyvius kreipinius, argumentą sumažindamos tik pastoviu
dydžiu. Tai lemia eksponentinį sudėtingumą.
– kiekviena jų
atlieka du rekursyvius kreipinius, argumentą sumažindamos tik pastoviu
dydžiu. Tai lemia eksponentinį sudėtingumą.
Rekursijos užbaigimas¶
Yra jūroj paskandinta dėžė, toj dėžėj yra zuikis,tam zuiky – karvelis, tam karvely – kiaušinis,tam kiaušiny – adata, ją perlaužus raganius mirs.Lietuvių liaudies pasaka
Kiekvienoje rekursinėje procedūroje turi būti numatyti visi ribiniai atvejai, kuriuos pasiekus rekursija nutraukiama. Ribinis atvejis – randama ir sulaužoma adata – numatytas netgi pasakoje, tuo labiau jo nereiktų pamiršti programuojant.
Panagrinėkime analizuotų pavyzdžių ribinius atvejus. Skaičiuojant
skaičiaus  faktorialą, ribinis atvejis yra
faktorialą, ribinis atvejis yra
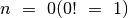 , ieškant
, ieškant  -ojo Fibonačio skaičiaus
–
-ojo Fibonačio skaičiaus
– 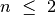 (
(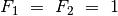 ). Ieškant
didžiausiojo bendro skaičių
). Ieškant
didžiausiojo bendro skaičių  ir
ir 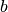 daliklio –
rekursija baigiama, kai
daliklio –
rekursija baigiama, kai 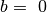 , keliant diskus Hanojaus bokštų
uždavinyje – kai reikia perkelti 0 (t. y. nebereikia kelti nė
vieno) diskų.
, keliant diskus Hanojaus bokštų
uždavinyje – kai reikia perkelti 0 (t. y. nebereikia kelti nė
vieno) diskų.
Viena vertus, būtina užtikrinti, kad rekursiniame procese būtinai bus pasiekiamas kuris nors ribinis atvejis, kita vertus – reikia nepamiršti numatyti visų ribinių atvejų. Jei karalaitis kiaušinyje rastų ne adatą, o obuolį, jis atsidurtų keblioje padėtyje…
Išnašos
- 1
Mengerio kempinės iliustracija paimta iš http://en.wikipedia.org/wiki/Menger_sponge.
- 2
Terminą „fraktalas“ (išvertus iš lotynų kalbos tai reiškia sudužęs, suskilęs) pasiūlė B. Mandelbrotas. Jis norėjo viena sąvoka aprašyti tokius gamtoje pasitaikančius darinius kaip debesys, kalnai, žaibai arba tam tikrus geometrinius objektus. Pasirodo, visi šie objektai yra fraktalai ir turi tam tikrų bendrų savybių. Fraktalų geometrijos atradimas yra vienas didžiausių XX amžiaus matematikos pasiekimų, ši geometrija plačiai taikoma įvairiose srityse, pavyzdžiui, kuriant fantastinius gamtą imituojančius peizažus filmuose.
- 3
Fibonačio skaičius galima skaičiuoti efektyviai (per tiesinį laiką), masyve įsimenant jau apskaičiuotas reikšmes; apie tai skaitykite Dinaminio programavimo principai skyrelyje.
- 4
Kelių paprastų uždavinio atvejų sprendimas ranka įtraukia mus į užduotį, suteikia intuicijos ir dažnai privilioja geras idėjas! Taigi tai naudinga daryti olimpiadose.