Perrinkimas ir grįžimo metodas¶
Modern computers are so fast that brute force can be an effective andhonourable way to solve problems.Šiuolaikiniai kompiuteriai yra tokie spartūs, kad perrinkimas gali būtiefektyvus ir garbingas būdas uždaviniams spręsti.Steven S. Skienna, Miguel A. Revilla, „Programming Challenges“
1852 metais matematikas F. Gatris (Francis Guthrie) paskelbė hipotezę, teigiančią, jog kiekvienam žemėlapiui nuspalvinti taip, kad jokios dvi gretimos valstybės nebūtų nuspalvintos ta pačia spalva, pakanka keturių spalvų. Daugelis matematikų siūlė šios hipotezės įrodymus, tačiau vis išaiškėdavo, kad jie neteisingi 1. Hipotezė pagaliau tapo teorema (buvo įrodyta) 1976 metais, o dalis įrodymo rėmėsi kompiuteriu išnagrinėtomis 1476 situacijomis. Kompiuterio programa veikė šimtus valandų, o žmonėms nepakako ir šimto metų. Taigi nors perrinkimo metodai dažnai būna neefektyvūs, spartėjant kompiuteriams šis sprendimo būdas (visų galimų sprendinių išbandymas) tam tikrais atvejais gali būti priimtinas, ypač jei perrinkimą pavyksta optimizuoti.
Formaliai perrinkimą galima apibrėžti kaip uždavinių sprendimo metodą, kai išbandomi visi galimi sprendiniai.
Šiame skyrelyje susipažinsime su patogiu metodu perrinkimui realizuoti
– grįžimo metodu. Grįžimo metodas (angl. Backtracking) –
tai sistemingas būdas spręsti uždaviniams, kurių sprendinys yra
kintamųjų 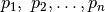 reikšmių rinkinys,
tenkinantis kokius nors reikalavimus. Prisiminkime, pavyzdžiui,
Keliaujančio pirklio uždavinį 2: šiuo atveju kintamųjų
reikšmių rinkinys,
tenkinantis kokius nors reikalavimus. Prisiminkime, pavyzdžiui,
Keliaujančio pirklio uždavinį 2: šiuo atveju kintamųjų
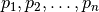 reikšmėms reikia priskirti skirtingus
miestų numerius taip, kad ši miestų aplankymo tvarka ir būtų
pageidaujamas maršrutas.
reikšmėms reikia priskirti skirtingus
miestų numerius taip, kad ši miestų aplankymo tvarka ir būtų
pageidaujamas maršrutas.
Pagrindinė grįžimo metodo idėja tokia: paeiliui renkamos visų galimų kintamųjų reikšmės ir tikrinama, ar tenkinami reikalavimai, o radus sprendinį arba situaciją, kai reikalavimai netenkinami, grįžtama per vieną žingsnį atgal ir parenkama nauja atitinkamo kintamojo reikšmė.
Programuojant grįžimo metodą dažnai naudojama rekursija. Panagrinėsime abstrakčių kombinatorinių uždavinių sprendimų schemas bei porą konkrečių uždavinių.
Kėlinių generavimas¶
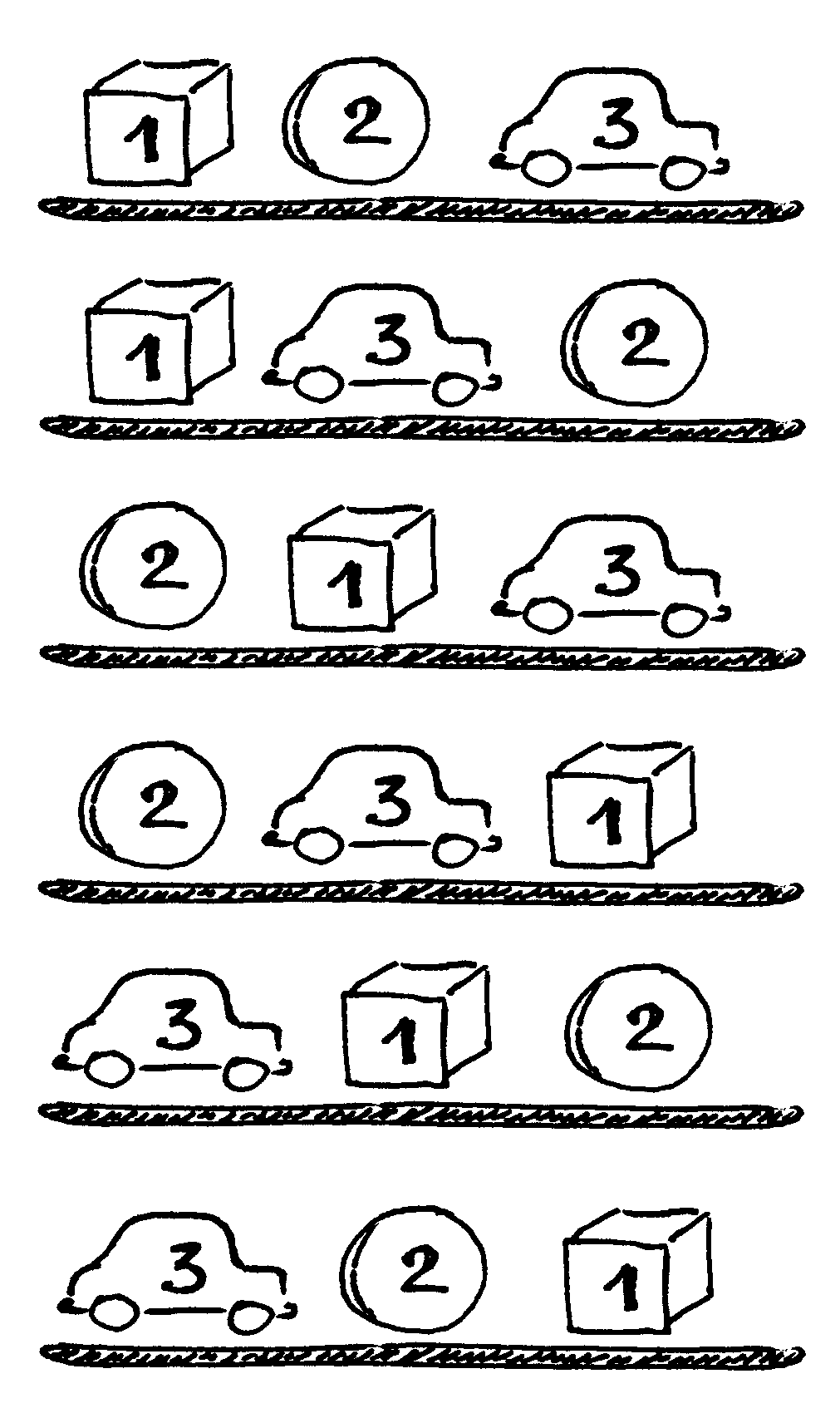
Fig. 11 Visi galimi trijų prekių išdėstymo lentynoje būdai¶
Sakykime, parduotuvės lentynoje vienoje eilėje reikia išdėlioti
 skirtingų prekių. Raskime visus skirtingus būdus, kaip tai
padaryti. Uždavinys yra ekvivalentus visų
skirtingų prekių. Raskime visus skirtingus būdus, kaip tai
padaryti. Uždavinys yra ekvivalentus visų  ilgio kėlinių be
pasikartojimų generavimo uždaviniui.
ilgio kėlinių be
pasikartojimų generavimo uždaviniui.
Kas gi tas kėlinys be pasikartojimų? Tarkime, turime aibę iš
 elementų. Kiekviena visų (skirtingų)
elementų. Kiekviena visų (skirtingų)  elementų
seka vadinama kėliniu be pasikartojimų. Taigi kėliniai vienas nuo
kito skiriasi tik elementų išsidėstymu vienas kito atžvilgiu.
elementų
seka vadinama kėliniu be pasikartojimų. Taigi kėliniai vienas nuo
kito skiriasi tik elementų išsidėstymu vienas kito atžvilgiu.
Parašykime algoritmą, kuris išspausdintų visus prekių išdėstymo
būdus. Prekes laikysime sunumeruotomis nuo 1 iki  .
.
Atkreipkite dėmesį – šis uždavinys priskiriamas įžangoje
minėtai uždavinių klasei: 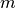 -ojoje vietoje padėtą prekę
(prekės numerį) pažymėjus
-ojoje vietoje padėtą prekę
(prekės numerį) pažymėjus 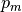 , reikia rasti kintamųjų
, reikia rasti kintamųjų
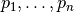 reikšmių (kintančių nuo 1 iki
reikšmių (kintančių nuo 1 iki  )
rinkinius, tenkinančius vieną reikalavimą – visos reikšmės turi
būti skirtingos; tuos rinkinius atspausdinti.
)
rinkinius, tenkinančius vieną reikalavimą – visos reikšmės turi
būti skirtingos; tuos rinkinius atspausdinti.
Uždavinį galima išreikšti rekursyviai, t. y. suskaidyti į tokius pat,
tik mažesnius, uždavinius. Tegu procedūra generuok(m, n) priskirs
reikšmes kintamiesiems nuo 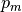 -ojo iki
-ojo iki 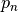 -ojo. Tuomet
jos veikimas galėtų būti toks:
-ojo. Tuomet
jos veikimas galėtų būti toks:
Jei
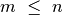 , imti po vieną visas dar lentynoje nepadėtas
prekes ir su kiekviena atlikti tokius veiksmus:
, imti po vieną visas dar lentynoje nepadėtas
prekes ir su kiekviena atlikti tokius veiksmus:Prekę padėti į
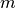 -ąją poziciją lentynoje (
-ąją poziciją lentynoje (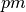 := prekės numeris).
:= prekės numeris).Sudėti į lentyną likusias prekes (priskirti reikšmes kintamiesiems nuo
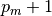 iki
iki 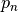 ) – toks pat
uždavinys, taigi iškviesti
) – toks pat
uždavinys, taigi iškviesti generuok(m + 1).Prekę, esančią
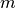 -ojoje pozicijoje, paimti nuo
lentynos.
-ojoje pozicijoje, paimti nuo
lentynos.
Jei
 , tai ši procedūra iškviesta jau išdėliojus
visas prekes lentynoje, todėl atspausdiname kintamųjų
, tai ši procedūra iškviesta jau išdėliojus
visas prekes lentynoje, todėl atspausdiname kintamųjų
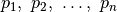 reikšmes.
reikšmes.
Norint patikrinti, kurios prekės jau sudėtos į lentyną, galima
peržiūrėti jau priskirtas reikšmes. Tačiau paprasčiau ir
efektyviau paskirti globalų loginį masyvą panaudotas, ir,
padėjus į lentyną prekę su numeriu i, pažymėti, jog šis
numeris jau panaudotas (panaudotas[i] := true), o paėmus prekę
nuo lentynos – atstatyti buvusią reikšmę
(panaudotas[i] := false).
const MAXN = 20; { didžiausia n reikšmė }
var p : array [1..MAXN] of integer;
panaudotas : array [1..MAXN] of boolean;
procedure spausdink(m: integer);
var i : integer;
begin
for i := 1 to m do
write(p[i], ' ');
writeln;
end;
procedure generuok(m, { parenkamas elementas m-ajai pozicijai }
n : integer);
var i : integer;
begin
{ jei m > n, tai ši procedūra iškviesta jau sugeneravus visą kėlinį }
if m > n then
spausdink(n)
else
for i := 1 to n do
if not panaudotas[i] then begin
panaudotas[i] := true;
p[m] := i;
generuok(m + 1, n);
panaudotas[i] := false;
end;
end;
const int MAXN = 20;
int p[MAXN];
bool panaudotas[MAXN+1];
// atspausdina sugeneruotą kėlinį
void spausdink(int n) {
for(int i = 0; i < n; i++) {
cout << p[i] << " ";
}
cout << endl;
}
// n – elementų kiekis
// k – dabar nagrinėjamo elemento indeksas
void gen(int n, int k) {
if(k >= n) {
spausdink(n);
return;
}
for(int i = 1; i <= n; i++) {
if(!panaudotas[i]) {
panaudotas[i] = true;
p[k] = i;
gen(n, k+1);
p[k] = 0;
panaudotas[i] = false;
}
}
}
Kad galėtume išspausdinti visas trijų prekių išdėliojimo lentynoje tvarkas, įvykdome:
n := 3;
for i := 1 to n do
panaudotas[i] := false;
generuok(1, n);
int n = 3;
for(int i = 1; i <= n; i++)
panaudotas[i] = false;
gen(n, 0);

Fig. 12 Procedūros generuok vykdymą vaizduojantis medis (n = 3)¶
Parašytą procedūrą nesunku pritaikyti kitiems uždaviniams – vietoj spausdinimo galima atlikti kokius nors kitus veiksmus. Spausdinimą iškėlėme į atskirą procedūrą norėdami paryškinti sprendimo struktūrą.
Koks gi parašytos programos sudėtingumas, t. y. kaip atliekamų
veiksmų skaičius priklauso nuo n? Algoritmas generuoja visus įmanomus
skaičių nuo 1 iki  išdėstymo į eilę būdus. Kiek jų yra?
Pirmąjį skaičių galima parinkti
išdėstymo į eilę būdus. Kiek jų yra?
Pirmąjį skaičių galima parinkti  būdų, antrąjį
skaičių –
būdų, antrąjį
skaičių – 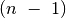 būdu (kadangi vienas skaičius jau
pasirinktas), trečiąjį skaičių –
būdu (kadangi vienas skaičius jau
pasirinktas), trečiąjį skaičių – 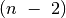 būdais (du
skaičiai jau parinkti) ir t. t. Gauname, kad yra
būdais (du
skaičiai jau parinkti) ir t. t. Gauname, kad yra
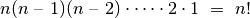 skirtingų būdų išdėstyti
skirtingų būdų išdėstyti  skaičių į eilę. Taigi
procedūros
skaičių į eilę. Taigi
procedūros generuok sudėtingumas yra 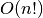 . Pavyzdžiui,
kai
. Pavyzdžiui,
kai 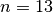 , tai vieną atspausdintą eilutę sudaro apie 30 simbolių, o
eilučių yra
, tai vieną atspausdintą eilutę sudaro apie 30 simbolių, o
eilučių yra 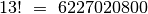 ir programa spausdintų daugiau
nei 150 gigabaitų teksto… (jei, žinoma, sulauktume veikimo
pabaigos).
ir programa spausdintų daugiau
nei 150 gigabaitų teksto… (jei, žinoma, sulauktume veikimo
pabaigos).
Aštuonių valdovių uždavinys¶
Išspręsime klasikinį aštuonių valdovių uždavinį.
Užduotis.
dydžio šachmatų lentoje reikia išdėlioti 8 valdoves taip, kad jokiu būdu neatsidurtų dvi vienoje eilutėje, stulpelyje arba įstrižainėje (t. y. nė viena negalėtų nukirsti kitos tolesniu ėjimu). Uždavinio formuluotę išplėsime ir ieškosime, kaip
valdovių surikiuoti
dydžio lentoje.
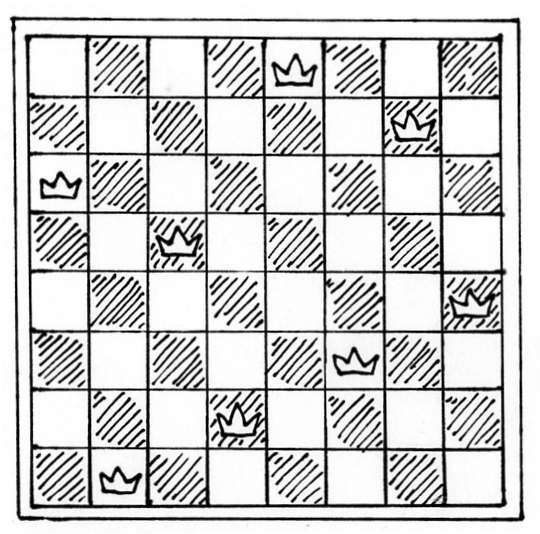
Fig. 13 Aštuonių valdovių išdėstymo pavyzdys¶
Šį uždavinį taip pat spręsime grįžimo metodu. Pavyzdžiui, lentos
langelius sunumeravę nuo 1 iki 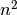 , kiekvienai valdovei galime
skirti po vieną langelį (numerį) taip, kad būtų tenkinama
uždavinio sąlyga. Tačiau spręsdami uždavinį šiuo būdu, turėtume
išnagrinėti labai didelį variantų skaičių. Variantų skaičius,
kuriuo aštuonioms valdovėms galima paskirstyti langelių numerius nuo
1 iki 64 yra
, kiekvienai valdovei galime
skirti po vieną langelį (numerį) taip, kad būtų tenkinama
uždavinio sąlyga. Tačiau spręsdami uždavinį šiuo būdu, turėtume
išnagrinėti labai didelį variantų skaičių. Variantų skaičius,
kuriuo aštuonioms valdovėms galima paskirstyti langelių numerius nuo
1 iki 64 yra
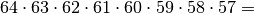
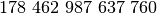 būdų.
būdų.
Be abejo, didžioji dalis šių variantų visiškai neįdomūs, nes labai tikėtina, kad kurios nors dvi valdovės atsidurs toje pačioje eilutėje, stulpelyje arba įstrižainėje. Atkreipkime dėmesį – kiekviename stulpelyje turės atsidurti lygiai viena valdovė; stulpelių yra tiek, kiek ir valdovių, o viename stulpelyje dvi valdovės stovėti negali.
Taigi galima šiek tiek kitaip vykdyti perrinkimą. Tegu 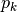 yra
valdovės, stovinčios
yra
valdovės, stovinčios  -ajame stulpelyje, eilutės numeris.
Kintamiesiems
-ajame stulpelyje, eilutės numeris.
Kintamiesiems 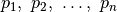 reikia priskirti reikšmes
nuo 1 iki
reikia priskirti reikšmes
nuo 1 iki  taip, kad jokios dvi valdovės neatsidurtų vienoje
eilutėje arba įstrižainėje.
taip, kad jokios dvi valdovės neatsidurtų vienoje
eilutėje arba įstrižainėje.
Šitaip atliekant perrinkimą, net nepaisant įstrižainių apribojimo,
nagrinėjamų variantų bus tik 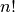 . Palyginkite – aštuonių
valdovių atveju teks išnagrinėti
. Palyginkite – aštuonių
valdovių atveju teks išnagrinėti 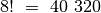 variantų
vietoj
variantų
vietoj 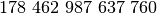 .
.
Perrenkant valdovių rikiavimo būdus, visai nesudėtinga sekti, kuriose eilutėse valdovės jau pastatytos – tam galima skirti loginį masyvą.
Tačiau kaip elgtis su įstrižainėmis? Patikrinti, ar dvi valdovės nestovi vienoje įstrižainėje, galima sustačius visas valdoves. Tačiau išsisuksime paprasčiau (ir efektyviau) pastebėję, kad įstrižaines taip pat nesunku sunumeruoti: vienoje įstrižainėje esančių langelių eilutės ir stulpelio numerių suma arba skirtumas yra pastovus.
Taigi žinodami langelio koordinates (stulpelio ir eilutės numerius),
galime pasakyti, kuriai įstrižainei priklauso šis langelis.
Įstrižainėms skiriame du loginius masyvus su indeksais atitinkamai
[2..2n] ir [-n + 1..n - 1], kuriuose žymėsime, ar
įstrižainės jau užimtos.
1 |
2 |
3 |
4 |
5 |
1 |
2 |
3 |
4 |
5 |
||||
1 |
2 |
3 |
4 |
5 |
6 |
1 |
0 |
-1 |
-2 |
-3 |
-4 |
||
2 |
3 |
4 |
5 |
6 |
7 |
2 |
1 |
0 |
-1 |
-2 |
-3 |
||
3 |
4 |
5 |
6 |
7 |
8 |
3 |
2 |
1 |
0 |
-1 |
-2 |
||
4 |
5 |
6 |
7 |
8 |
9 |
4 |
3 |
2 |
1 |
0 |
-1 |
||
5 |
6 |
7 |
8 |
9 |
10 |
5 |
4 |
3 |
2 |
1 |
0 |
Parašysime procedūrą statyk(k, n), perrenkančią sprendinius
grįžimo metodu, kuri visais įmanomais būdais sudėlios lentoje
valdoves nuo  -osios iki
-osios iki  -osios.
-osios.  -oji valdovė
bus statoma
-oji valdovė
bus statoma  -ajame stulpelyje. Taigi procedūra turi bandyti
pastatyti
-ajame stulpelyje. Taigi procedūra turi bandyti
pastatyti  -ąją valdovę nepažeisdama apribojimų, o
pastačius – pažymėti užimtas eilutę ir įstrižaines, ir
iškviesti
-ąją valdovę nepažeisdama apribojimų, o
pastačius – pažymėti užimtas eilutę ir įstrižaines, ir
iškviesti statyk(k + 1, n).
Jei iškvietus procedūrą parametro  reikšmė viršija
reikšmė viršija
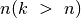 , tai reiškia, kad ši procedūra buvo iškviesta
sudėliojus visas
, tai reiškia, kad ši procedūra buvo iškviesta
sudėliojus visas  valdovių, taigi radus sprendinį. Viena
vertus, sudėliojus visas
valdovių, taigi radus sprendinį. Viena
vertus, sudėliojus visas  valdovių, procedūros statyk būtų
galima nebekviesti, tačiau dėl šio papildomo iškvietimo programa
tampa paprastesnė ir aiškesnė. Tai dažnai naudojama rekursyviose
procedūrose.
valdovių, procedūros statyk būtų
galima nebekviesti, tačiau dėl šio papildomo iškvietimo programa
tampa paprastesnė ir aiškesnė. Tai dažnai naudojama rekursyviose
procedūrose.
Procedūroje skaičiuosime, kiek yra sprendinių, t. y. būdų išdėlioti valdoves lentoje. Tačiau nesunku modifikuoti procedūrą taip, kad ši rastus sprendinius išspausdintų – tuomet dar reikėtų saugoti, kur lentoje statomos valdovės.
const MAXN = 12;
var eilutė : array [1..MAXN] of boolean;
įstr1 : array [2..2 * MAXN] of boolean;
įstr2 : array [-MAXN + 1..MAXN - 1] of boolean;
sprendinių_sk : longint;
procedure statyk(k, { valdovė statoma k-ajame stulpelyje }
n : integer { reikia pastatyti n valdovių });
var i : integer;
begin
if k > n then { rastas sprendinys }
sprendinių_sk := sprendinių_sk + 1
else
for i := 1 to n do
if not (eilutė[i] or
įstr1[i + k] or
įstr2[i - k])
then begin
eilutė[i] := true;
įstr1[i + k] := true;
įstr2[i - k] := true;
{ bandoma pastatyti likusias valdoves }
statyk(k + 1, n);
eilutė[i] := false;
įstr1[i + k] := false;
įstr2[i - k] := false;
end;
end;
const int MAXN = 12;
bool eil[MAXN];
bool istr1[2*MAXN];
bool istr2[2*MAXN];
long long sprendiniųSk;
// padeda karalienę langelyje (r, c)
// r - eilutės numeris
// c - stulpelio numeris
// reikšmė – true, jei padedame karalienę; false, jei nuimame
void padėti(int n, int r, int c, bool reikšmė) {
eil[r] = reikšmė;
istr1[r+c] = reikšmė;
istr2[r-c+n-1] = reikšmė; // pridedam n-1, kad numeracija pasidarytu nuo 0, o ne nuo neigiamų skaičių
}
// ar langelis (r, c) nėra kertamas jokios karalienės?
// r - eilutės numeris
// c - stulpelio numeris
bool arLaisvas(int n, int r, int c) {
return !eil[r] && !istr1[r+c] && !istr2[r-c+n-1];
}
// n - kiek iš viso valdovių
// c - kuriame stulpelyje dabar statome valdovę
void statyk(int n, int c) {
if(c >= n) {
sprendiniųSk++;
return;
}
for(int r = 0; r < n; r++) {
if(arLaisvas(n, r, c)) {
padėti(n, r, c, true);
statyk(n, c+1);
padėti(n, r, c, false);
}
}
}
// funkcijos kvietimas main funkcijoje:
statyk(n, 0);

Fig. 14 Valdovių uždavinio rekursijos medis, kai n=4¶
Gretiniai, deriniai ir poaibiai¶
Fig. 15 Azartiniai žaidimai buvo dingstis atsirasti kombinatorikai¶
Ankstesniame skyrelyje (Kėlinių generavimas) nagrinėjome, kiek ir kokių kombinacijų galima sudaryti iš įvairių objektų, kad būtų tenkinamos vienokios ar kitokios sąlygos. Šitai nagrinėja matematikos šaka, vadinama kombinatorika, kuri atsirado XVI amžiuje išpopuliarėjus azartiniams žaidimams. Pirmieji kombinatorikos uždaviniai ir buvo susiję su šiais žaidimais, pavyzdžiui, buvo tiriama, keliais būdais galima išmesti kokį nors taškų skaičių, žaidžiant dviem arba trimis kauliukais.
Kombinatorikos žinių prireikia sprendžiant įvairius olimpiadinius uždavinius. Šiame skyrelyje glaustai išdėstysime, kaip generuoti kitus junginius rekursiniais algoritmais 3.

Fig. 16 Keletas gretinių iš penkių prekių po tris¶
Gretiniai. Grįžkime prie pavyzdžio su parduotuve. Sakykime,
turime  skirtingų prekių, kurias reikia išdėlioti
lentynoje; deja, lentynoje telpa tik
skirtingų prekių, kurias reikia išdėlioti
lentynoje; deja, lentynoje telpa tik  prekių ir visų prekių
iš karto parodyti pirkėjams nepavyks. Reikia rasti visus būdus,
kuriais galima išdėlioti prekes lentynoje. Tuščių vietų likti
lentynoje negali.
prekių ir visų prekių
iš karto parodyti pirkėjams nepavyks. Reikia rasti visus būdus,
kuriais galima išdėlioti prekes lentynoje. Tuščių vietų likti
lentynoje negali.
Kitaip sakant, reikia rasti visus gretinius be pasikartojimų iš
 elementų po
elementų po  . Uždavinys labai panašus į jau
nagrinėtą kėlinių be pasikartojimų generavimo uždavinį, tiesiog
iš
. Uždavinys labai panašus į jau
nagrinėtą kėlinių be pasikartojimų generavimo uždavinį, tiesiog
iš  elementų renkame tik
elementų renkame tik 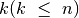 .
.
const MAX = 20; { didžiausia n ir k reikšmė }
var p : array [1..MAX] of integer;
panaudotas : array [1..MAX] of boolean;
procedure generuok(m, { parenkamas elementas m-ajai pozicijai }
n, k : integer);
var i : integer;
begin
{ jei m > k,
tai ši procedūra iškviesta jau sugeneravus visą gretinį }
if m > k then
spausdink(k) { procedūros spausdink tekstą rasite 5.1 skyrelyje }
else
for i := 1 to n do
if not panaudotas[i] then begin
panaudotas[i] := true;
p[m] := i;
generuok(m + 1, n, k);
panaudotas[i] := false;
end;
end;
const int MAXN = 20;
int p[MAXN];
bool panaudotas[MAXN+1];
void gen(int m, int n, int k) {
if(m >= k) {
spausdink(k);
return;
}
for(int i = 1; i <= n; i++) {
if(!panaudotas[i]) {
panaudotas[i] = true;
p[m] = i;
gen(m+1, n, k);
p[m] = 0;
panaudotas[i] = false;
}
}
}
Norėdami gauti visus gretinius iš 5 po 3, į procedūrą kreipiamės:
n := 5;
k := 3;
for i := 1 to n do
panaudotas[i] := false;
generuok(1, n, k);
int n = 5;
int k = 3;
for(int i = 1; i <= n; i++)
panaudotas[i] = false;
gen(1, n, k);
Suskaičiuosime, kiek gali būti skirtingų gretinių be pasikartojimų,
tuo pačiu įvertinsime ir algoritmo sudėtingumą. Pirmąją prekę
galime rinktis iš visų  prekių, antrąją prekę – iš
prekių, antrąją prekę – iš
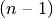 prekės ir t. t.
prekės ir t. t.  -ąją prekę galime
rinktis iš
-ąją prekę galime
rinktis iš 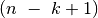 prekių.
prekių.
Gretinių be pasikartojimų iš  elementų po
elementų po  skaičius žymimas
skaičius žymimas 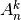 ir lygus
ir lygus
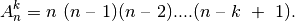
Deriniai. Generuodami gretinius atsižvelgėme į prekių išdėstymą
lentynose. Pamėginkime rasti visus būdus, kuriais galima išdėstyti
 skirtingų prekių lentynoje, kurioje telpa tik
skirtingų prekių lentynoje, kurioje telpa tik  prekių (lentynoje neturi likti tuščių vietų) nekreipiant dėmesio
į prekių išdėstymą, t. y. kai rūpi tik tai, kokios prekės yra
lentynoje, tačiau nesvarbu, kokia tvarka jos ten išdėliotos. Kitaip
sakant, reikia sugeneruoti visus derinius be pasikartojimų iš
prekių (lentynoje neturi likti tuščių vietų) nekreipiant dėmesio
į prekių išdėstymą, t. y. kai rūpi tik tai, kokios prekės yra
lentynoje, tačiau nesvarbu, kokia tvarka jos ten išdėliotos. Kitaip
sakant, reikia sugeneruoti visus derinius be pasikartojimų iš
 elementų po
elementų po  .
.
Derinius galima generuoti kaip gretinius, laikantis vienos papildomos
taisyklės: prekės dėliojamos taip, kad jų numeriai sudarytų didėjančią
seką, t. y. 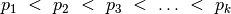 . Derinius
generuojančiai rekursinei procedūrai prireiks vieno papildomo
parametro, kuris rodytų, nuo kurio elemento galime rinkti tolesnius
elementus.
. Derinius
generuojančiai rekursinei procedūrai prireiks vieno papildomo
parametro, kuris rodytų, nuo kurio elemento galime rinkti tolesnius
elementus.
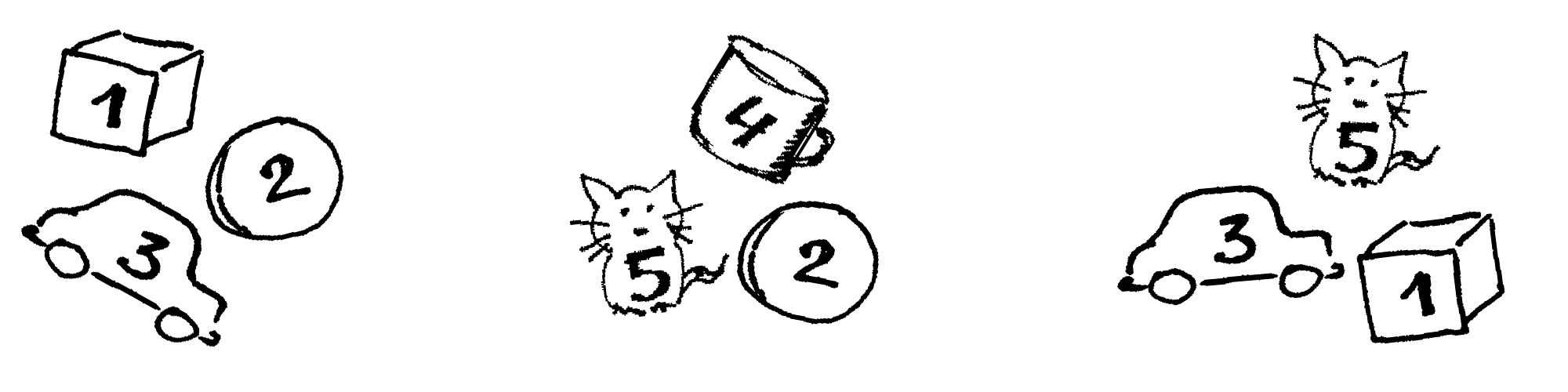
Fig. 17 Keletas derinių iš penkių prekių po tris (tvarka deriniuose nesvarbi)¶
const MAX = 20; { didžiausia n ir k reikšmė }
var p : array [1..MAX] of integer;
panaudotas : array [1..MAX] of boolean;
procedure generuok(nuo, { bus renkamasi tik iš elementų,
didesnių arba lygių „nuo“ }
m, { parenkamas elementas m-ajai pozicijai }
n, k: integer);
var i : integer;
begin
{ jei m > k, tai ši procedūra iškviesta jau sugeneravus visą derinį }
if m > k then spausdink(k) { procedūros spausdink tekstą rasite 5.1 skyrelyje }
else
for i := nuo to n do
if not panaudotas[i] then begin
panaudotas[i] := true;
p[m] := i;
generuok(i + 1, m + 1, n, k);
panaudotas[i] := false;
end;
end;
const int MAXN = 20;
int p[MAXN];
int panaudotas[MAXN+1];
void gen(int nuo, int m, int n, int k) {
if(m >= k) {
spausdink(k);
return;
}
for(int i = nuo; i <= n; i++) {
if(!panaudotas[i]) {
panaudotas[i] = true;
p[m] = i;
gen(i+1, m+1, n, k);
p[m] = 0;
panaudotas[i] = false;
}
}
}
Norėdami gauti visus skirtingus derinius iš 5 elementų po 3, į procedūrą kreipiamės:
n := 5;
k := 3;
for i := 1 to n do
panaudotas[i] := false;
generuok(1, 1, n, k);
int n = 5;
int k = 3;
for(int i = 1; i <= n; i++)
panaudotas[i] = false;
gen(1, n, k);
Beliko apskaičiuoti, kiek gali būti skirtingų derinių be
pasikartojimų iš  po
po  . Šį skaičių pažymėkime
. Šį skaičių pažymėkime
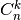 .
.
Sakykime, turime konkretų derinį. Jei paimtume visus jo perstatymus,
gautume visus kėlinius be pasikartojimų iš tų  derinį
sudarančių elementų. Tokių kėlinių gali būti
derinį
sudarančių elementų. Tokių kėlinių gali būti 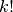
O jei kartu paimtume visus kiekvieno galimo derinio perstatymus, gautume
visus gretinius be pasikartojimų iš  elementų po
elementų po  .
Žinome, kad jų gali būti
.
Žinome, kad jų gali būti
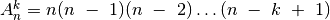 . Gauname:
. Gauname:
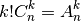
arba:
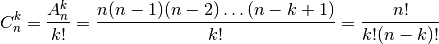
Pavyzdžiui, jei turime 10 prekių, o lentynoje telpa 7 prekės, tai
nepaisydami prekių išdėstymo tvarkos šias prekes galime išdėlioti
lentynoje
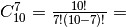
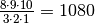 būdų.
būdų.
Poaibiai. Visus galimus  elementų aibės poaibius galime
gauti generuodami iš eilės
elementų aibės poaibius galime
gauti generuodami iš eilės 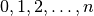 ilgio derinius be
pasikartojimų. Galimas ir dar paprastesnis būdas: pakanka sugeneruoti
visus įmanomus žodžius, kurių ilgis
ilgio derinius be
pasikartojimų. Galimas ir dar paprastesnis būdas: pakanka sugeneruoti
visus įmanomus žodžius, kurių ilgis  iš abėcėlės
iš abėcėlės
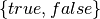 .
.
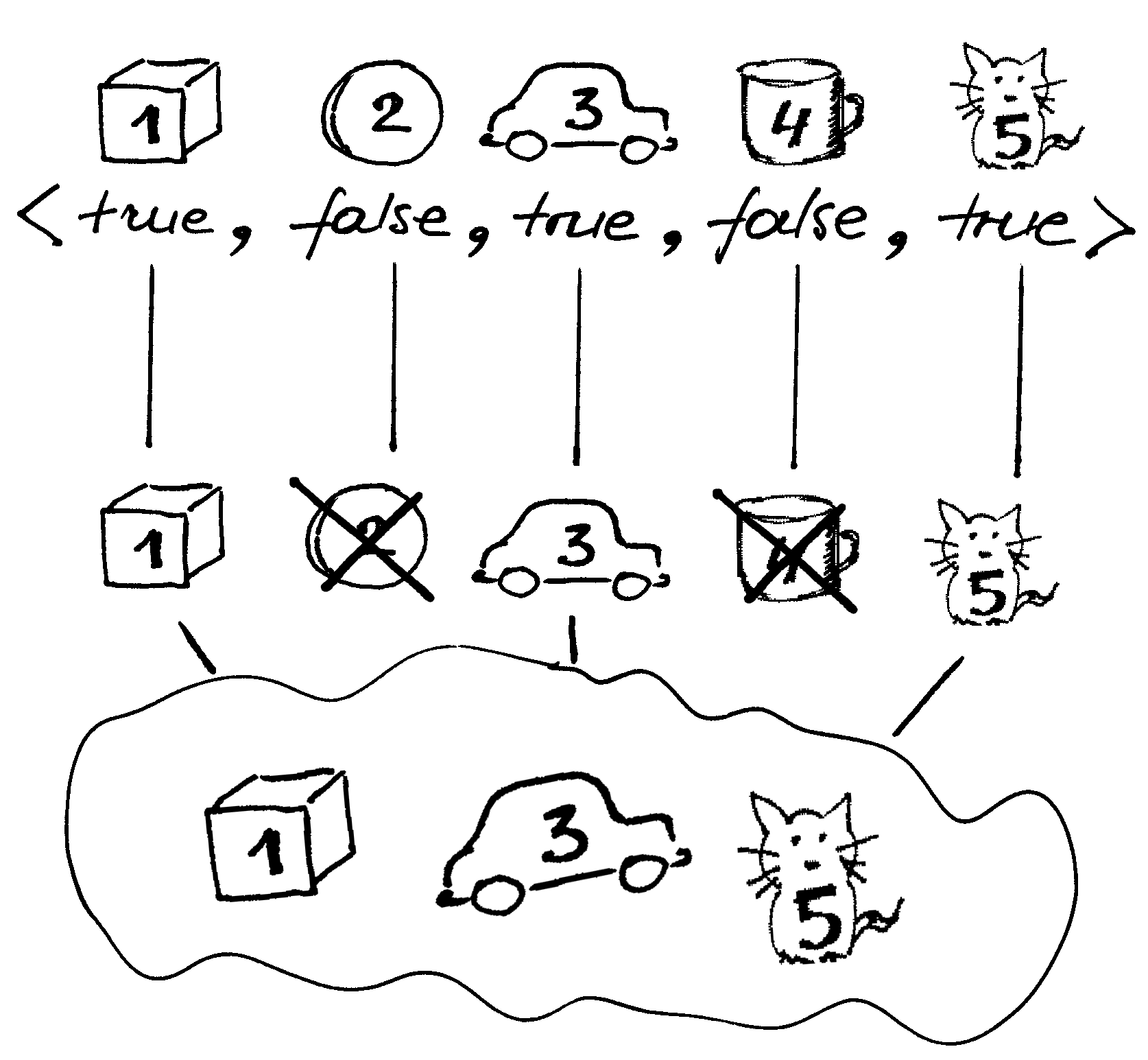
Fig. 18 Abėcėlės {true, false} žodžių transformavimo į poaibius pavyzdys¶
const MAXN = 20; { didžiausia n reikšmė }
var parinktas : array [1..MAXN] of boolean;
procedure spausdink (m: integer);
var i : integer;
begin
write('{ ');
for i := 1 to m do
if parinktas[i] then
write(i, ' ');
writeln('}');
end;
procedure generuok(k, n : integer);
{ nagrinėjamas k-asis n elementų aibės narys }
var log : boolean;
begin
{ jei k > n, tai ši procedūra iškviesta jau sugeneravus visą poaibį }
if k > n then
spausdink (k)
else
for log := false to true do begin
parinktas[k] := log;
generuok(k + 1, n);
end;
end;
const int MAXN = 20;
bool parinktas[MAXN];
void spausdink(int m) {
cout << "{";
for(int i = 0; i < m; i++) {
if(parinktas[i]) {
cout << i << " ";
}
}
cout << "}" << endl;
}
void gen(int k, int n) {
if(k >= n) {
spausdink(n);
return;
}
for(int log = 0; log <= 1; log++) {
parinktas[k] = log;
gen(k+1, n);
}
}
Norėdami gauti visus poaibius iš 4 elementų, į procedūrą
generuok kreipiamės:
n := 4;
generuok(1, n);
int n = 4;
gen(0, n);
Suskaičiuosime, kiek skirtingų poaibių turės aibė iš  elementų, o tuo pačiu ir algoritmo sudėtingumą. Poaibių skaičius
lygus visų įmanomų
elementų, o tuo pačiu ir algoritmo sudėtingumą. Poaibių skaičius
lygus visų įmanomų  ilgio žodžių iš abėcėlės
ilgio žodžių iš abėcėlės
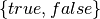 skaičiui. Kadangi kiekvieną tokio žodžio
raidę galime parinkti dviem būdais (atitinkamas elementas arba
įtraukiamas į poaibį, arba ne), tai tokių žodžių (ir galimų
poaibių) skaičius lygus
skaičiui. Kadangi kiekvieną tokio žodžio
raidę galime parinkti dviem būdais (atitinkamas elementas arba
įtraukiamas į poaibį, arba ne), tai tokių žodžių (ir galimų
poaibių) skaičius lygus 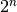 .
.
Uždavinys Pakyla 4¶
Panagrinėsime vieną uždavinį, kurio sprendimui reikia taikyti kombinatorikos žinias ir perrinkti visus įmanomus variantus.
Tarp dviejų taškų
ir
norime pastatyti pakylą, kurios aukštis
metrų. Į pakylos viršų tiek iš taško
, tiek iš taško
turi vesti kylantys laiptai. Laiptų pakopos aukštis yra 1 metras. Nesunku apskaičiuoti, kad pakylą turi sudaryti
pakopų – po
iš kiekvienos pusės bei viršutinė. Pirmoji laiptų, kylančių iš taško
(taško
), pakopa turi prasidėti taške
(atitinkamai taške
).
Atstumas tarp taškų
ir
lygus
metrų. O kiekvienos pakopos plotis turi būti lygus sveikajam metrų skaičiui. Aukščiausioje dalyje esančios pakopos plotis turi būti lygus
metrų.
Užduotis. Reikia rasti visus galimus skirtingus būdus pakylai įrengti. Dvi pakylos laikomos skirtingomis, jei jų aukštis skiriasi bent vienoje pozicijoje tarp taškų
ir
.
Galioja ribojimai: pradiniai duomenys tokie, kad galimų variantų skaičius pakylai įrengti neviršija
.
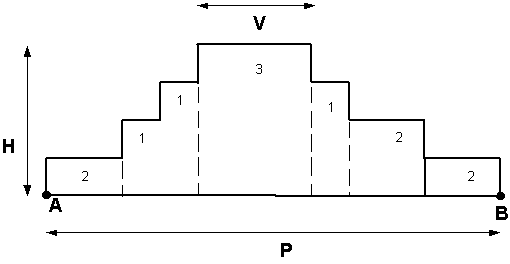
Fig. 19 Pakylos pavyzdys. 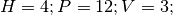 Ši pakyla apibūdinama seka:
Ši pakyla apibūdinama seka: 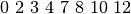 ¶
¶
Prieš sprendžiant uždavinį, svarbu tiksliai apibrėžti, ko iš
tiesų ieškome. Kiekvieną galimą pakylą atitinka didėjanti
skaičių nuo  iki
iki 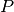 seka
seka 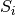 , kurią sudaro
lygiai
, kurią sudaro
lygiai 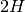 skaičių ir kuri tenkina papildomus ribojimus:
skaičių ir kuri tenkina papildomus ribojimus:
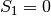 ;
;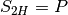 ;
;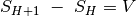 .
.
Kiekvienas šios sekos elementas rodo vietą (koordinatę 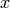 ),
kurioje keičiasi pakopos aukštis. Pavyzdžiui, paveiksle pavaizduotą
pakylą atitinka skaičių seka
),
kurioje keičiasi pakopos aukštis. Pavyzdžiui, paveiksle pavaizduotą
pakylą atitinka skaičių seka
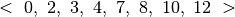 .
.
Taigi pirmojo ir paskutinio nario reikšmės yra fiksuotos, o
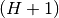 -ojo nario reikšmė priklauso nuo
-ojo nario reikšmė priklauso nuo 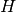 -ojo nario:
-ojo nario:
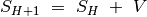 . Nesunku apriboti
. Nesunku apriboti  -ojo nario
reikšmę:
-ojo nario
reikšmę:
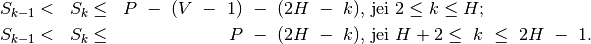
Apatinis ribojimas išplaukia iš to, kad seka yra didėjanti, o viršutinis – kad nepritrūktų skaičių sekai užbaigti.
Gavome derinių generavimo uždavinį, tik tam tikrais ribojimais maksimalioms pozicijų reikšmėms.
Pasinaudosime jau žinomu derinių generavimo algoritmu, kurį pritaikysime šio uždavinio sprendimui. Beje, sutarsime, kad sprendinys egzistuoja.
const MAXH = 100; { maksimalus pakylos aukštis }
var s : array [1..2*MAXH] of integer;
P, H, V : integer;
procedure generuok(k : integer);
{ generuoja sekos narį, kurio numeris k }
var i, max : integer;
begin
if k = 2*H then
{ sugeneruoti visi nariai (paskutinis žinomas iš anksto) }
spausdink(2*H) { Procedūra spausdink analogiška spausdinimo
procedūrai 5.1 skyrelyje. }
else if k = H+1 then begin
{ (H+1)-osios pakopos viršūnės plotis fiksuotas }
s[k] := s[k-1]+V;
generuok(k+1);
end
else begin
{ nagrinėjamos visos galimos k-ojo nario reikšmės }
if k <= H then
max := P-(2*H-k)-(V-1)
else
max := P-(2*H-k);
for i := s[k-1]+1 to max do begin
s[k] := i;
generuok(k+1);
end;
end;
end;
const int MAXH = 100;
int s[2*MAXH+1];
int P, H, V;
// generuoja sekos narį, kurio numeris k
void gen(int k) {
if (k == 2*H) {
spausdink(2*H);
} else if (k == H+1) {
// (H+1)-osios pakopos viršūnės plotis fiksuotas
s[k] = s[k-1] + V;
gen(k + 1);
} else {
// nagrinėjamos visos galimos k-ojo nario reikšmės
int mx;
if (k <= H)
mx = P-(2*H-k)-(V-1);
else
mx = P-(2*H-k);
for (int i = s[k-1]+1; i <= mx; i++) {
s[k] = i;
gen(k+1);
}
}
}
Į procedūrą generuok turi būti kreipiamasi tokiu būdu:
S[1] := 0;
S[2*H] := P;
generuok(2);
// Funkcija gen() turi būti iškviečiama tokiu būdu:
s[1] = 0
s[2*H] = P;
gen(2);
Perrinkimo optimizavimas¶
Panagrinėkime dar vieną pavyzdį. Sakykime, saugos kodą, kurį reikia
surinkti įeinant į laiptinę, sudaro 3 skaitmenys. Norint jį
atspėti, reikia išbandyti 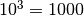 variantų. Jei vieną
kodą galima surinkti ir pabandyti atidaryti duris per 3 sekundes, tai
visus variantus pavyks išbandyti per 50 minučių. Tačiau jei saugos
kodą sudarytų 4 skaitmenys, tai visiems
variantų. Jei vieną
kodą galima surinkti ir pabandyti atidaryti duris per 3 sekundes, tai
visus variantus pavyks išbandyti per 50 minučių. Tačiau jei saugos
kodą sudarytų 4 skaitmenys, tai visiems 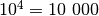 variantams išbandyti prireiktų daugiau nei 8 valandų. Matome, kad
pradiniams duomenims (t. y. skaitmenų skaičiui) padidėjus 33%,
galimų sprendinių skaičius padidėja 900%. Toks staigus sprendinių
skaičiaus augimas vadinamas kombinatoriniu sprogimu.
variantams išbandyti prireiktų daugiau nei 8 valandų. Matome, kad
pradiniams duomenims (t. y. skaitmenų skaičiui) padidėjus 33%,
galimų sprendinių skaičius padidėja 900%. Toks staigus sprendinių
skaičiaus augimas vadinamas kombinatoriniu sprogimu.
Vienas didžiausių perrinkimo trūkumų yra tai, kad susiduriama su kombinatoriniu sprogimu. Generuojant kombinatorinius objektus kitaip ir negali būti: reikia rasti visus objektus, o jų yra daug, taigi ir algoritmų sudėtingumas turi būti didelis. Tačiau dažniau tenka ieškoti tam tikros kombinacijos, t. y. sprendinio, tenkinančio konkrečias sąlygas.
Todėl daugelyje tokių uždavinių stengiamasi optimizuoti
paiešką. Vienas galimų optimizavimo būdų – paanalizuoti
sprendinio struktūrą ir sumažinti galimų sprendinių paieškos
erdvę. Taip darėme Aštuonių valdovių uždavinyje. Pradinė
sprendinių erdvė buvo gana didelė: buvo sutarta, kad kiekviena
valdovė gali stovėti bet kuriame lentos langelyje (po vieną valdovę
langelyje), ir galimų variantų skaičius viršijo
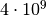 . Tačiau jei perrenkant variantus, kiekviena
valdovė statoma tik į tuščią eilutę – tai išnagrinėjamų
variantų skaičius iš karto sumažėja iki
. Tačiau jei perrenkant variantus, kiekviena
valdovė statoma tik į tuščią eilutę – tai išnagrinėjamų
variantų skaičius iš karto sumažėja iki 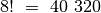 .
.
Gali pavykti sumažinti ir skyrelio pradžioje pateikto uždavinio
paieškos erdvę. Jei žinoma, kad visi skaičiai turi būti paspausti
vienu metu, tai saugos kode nebus pasikartojančių skaitmenų. Be to,
šitaip parenkant kodą nenustatoma skaitmenų tvarka, todėl galime dar
sumažinti sprendinių erdvę: pakanka išbandyti visus derinius.
Pavyzdžiui, bandant atspėti keturių skaitmenų saugos kodą, mus
domina visi deriniai iš 10 po 4. Jų skaičius yra
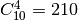 (palyginkite su
(palyginkite su 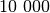 ).
).
Jei reikalingas tik vienas sprendinys, paiešką verta optimizuoti parenkant sprendinių nagrinėjimo tvarką taip, kad tikėtini sprendiniai būtų nagrinėjami pirmiausia, jei tik tai įmanoma padaryti.
Yra įvairiausių kitų metodų paieškai pagreitinti, dažnai priimtinų tik konkrečiam uždaviniui. Pavyzdžiui, ieškant geriausio ėjimo stalo žaidimuose, naudojama Minimax paieška su Alfa-Beta atkirtimu; šis metodas leidžia anksčiau atkirsti daug neperspektyvių paieškos medžio šakų.
- 1
Keletas įrodymų buvo paneigta praėjus tik 11 metų po jų paskelbimo.
- 2
Žr. skyrelį NP sudėtingumas.
- 3
Yra efektyvesnių (nerekursinių) kombinatorinius objektus generuojančių algoritmų, tačiau rekursiniai algoritmai yra intuityvesni ir lengviau realizuojami.
- 4
Šis uždavinys buvo pateiktas Lietuvos moksleivių informatikos olimpiadoje III etape 2004 metais.