Oilerio ir Hamiltono ciklai¶
The whole branch of mathematics was born out of the game.Iš žaidimų kilo net atskira matematikos šaka.Nežinomas autorius apie grafų teorijos atsiradimą
Pažintį su grafais pradėjome nuo istorijos apie septynių Karaliaučiaus tiltų uždavinį. Šiame skyrelyje papasakosime, kaip tą uždavinį išsprendė Oileris, taip pat išspręsime jau ne kartą sutiktą Hamiltono ciklų uždavinį.
Tam prireiks keleto naujų grafų teorijos sąvokų, tad nuo jų ir pradėkime.
Kelios grafų teorijos sąvokos¶
Briaunų, jungiančių viršūnę  su kokia nors kita
viršūne, skaičius vadinamas viršūnės
su kokia nors kita
viršūne, skaičius vadinamas viršūnės  laipsniu.
Paprastuose grafuose viršūnės laipsnis yra jai gretimų viršūnių
skaičius, tačiau multigrafuose (grafuose, kuriuose dvi viršūnes gali
jungti daugiau nei viena briauna), šie du skaičiai gali skirtis.
laipsniu.
Paprastuose grafuose viršūnės laipsnis yra jai gretimų viršūnių
skaičius, tačiau multigrafuose (grafuose, kuriuose dvi viršūnes gali
jungti daugiau nei viena briauna), šie du skaičiai gali skirtis.

Fig. 45 Grafo viršūnių laipsniai užrašyti šalia viršūnių;
grafas turi vienintelį tiltą – briauną 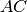 ¶
¶
Briauna, kurią pašalinus iš grafo padidėtų jungumo komponentų
skaičius, vadinama tiltu. Kitaip tariant, jei norėtume iš kurios
nors viršūnės pasiekti kitą, ir tam būtinai turėtume eiti
briauna 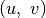 , ši briauna ir būtų tiltas.
, ši briauna ir būtų tiltas.
Oilerio keliai ir ciklai¶

Fig. 46 Šveicarų matematikas Leonardas Oileris (Leonhard Euler), 1707–1783¶
Jau minėjome, kad Oileris neigiamai atsakė į Karaliaučiaus gyventojus dominantį klausimą: nėra maršruto, kuris prasidėtų viename iš krantų, pereitų kiekvienu iš septynių tiltų lygiai vieną kartą ir baigtųsi tame pačiame krante. Išnagrinėjęs tokių maršrutų galimybę, Oileris padėjo grafų teorijos pagrindus.
Jam pavyko išspręsti šį uždavinį: Oileris nustatė, kokios sąlygos yra būtinos ir pakankamos, kad grafe egzistuotų toks maršrutas, be to, pateikė algoritmą jam rasti. Maršrutai, prasidedantys ir užsibaigiantys toje pačioje viršūnėje bei apeinantys visas grafo briaunas po vieną kartą, nuo tada vadinami Oilerio ciklais arba (jei baigiasi kitoje viršūnėje negu prasideda) Oilerio keliais.
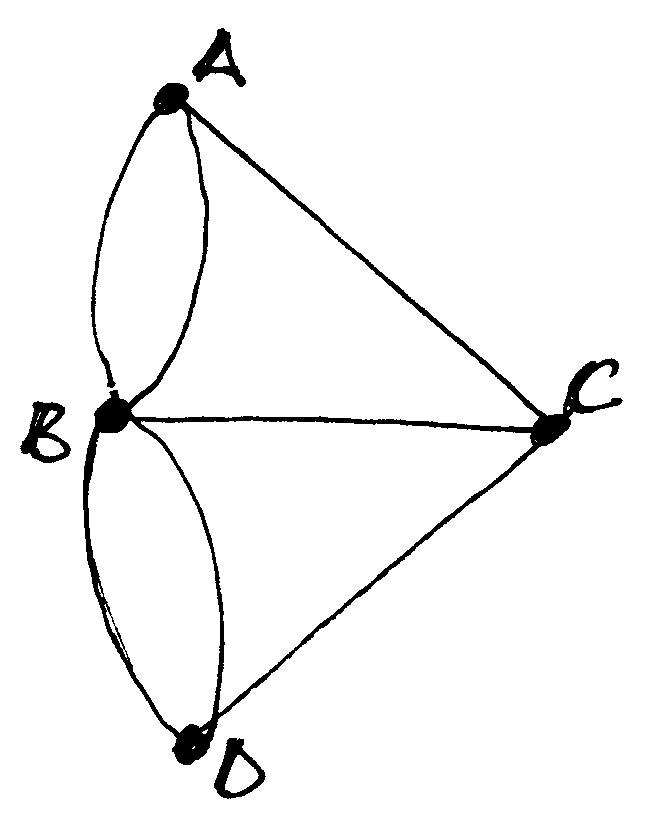
Fig. 47 Karaliaučiaus tiltų uždavinį atitinkantis grafas¶
Nėra sudėtinga Karaliaučiaus tiltų atveju įrodyti, kad neegzistuoja Oilerio ciklas. Prisiminkime, kaip atrodė grafas, kurio viršūnės – Karaliaučiaus salos ir krantai, o briaunos – juos jungiantys tiltai (Fig. 47 pav.).
Ieškome maršruto, kuris kiekviena briauna pereitų vieną kartą. Panagrinėjus kurią nors vieną viršūnę, nesunku pastebėti, jog ieškomas maršrutas neįmanomas, jei viršūnės laipsnis nelyginis: juk išeiti iš šios viršūnės turėsime lygiai tiek kartų, kiek ir atėjome, ir kiekvienąkart vis kita briauna, taigi visas briaunų skaičius turi būti dviejų kartotinis, lyginis. Tačiau šiame grafe visų viršūnių laipsniai nelyginiai (3, 3, 3 ir 5), taigi ir toks maršrutas tikrai neįmanomas.
Įrodėme, kad toks maršrutas negalimas, jei bent vienos viršūnės laipsnis nelyginis. Oileris įrodė griežtesnį teiginį: Oilerio ciklas egzistuoja tada ir tik tada, kai visų viršūnių laipsniai yra lyginiai.
O kaip su Oilerio keliais? Jei maršrutas turi baigtis ne toje pačioje viršūnėje kur prasidėjo, tai minėta taisyklė turi galioti visoms viršūnėms, išskyrus pradinę ir galinę. Oilerio kelias egzistuoja tada ir tik tada, kai lygiai dviejų viršūnių laipsniai yra nelyginiai.
Be abejo, grafai, turintys Oilerio ciklą arba kelią, turi pasižymėti dar viena natūralia savybe – jie turi būti jungūs 1
Flerio algoritmas¶
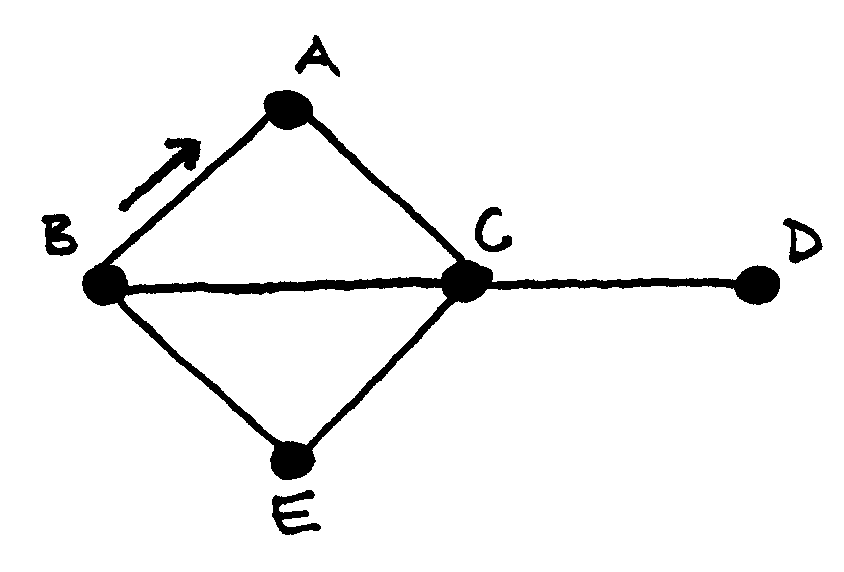
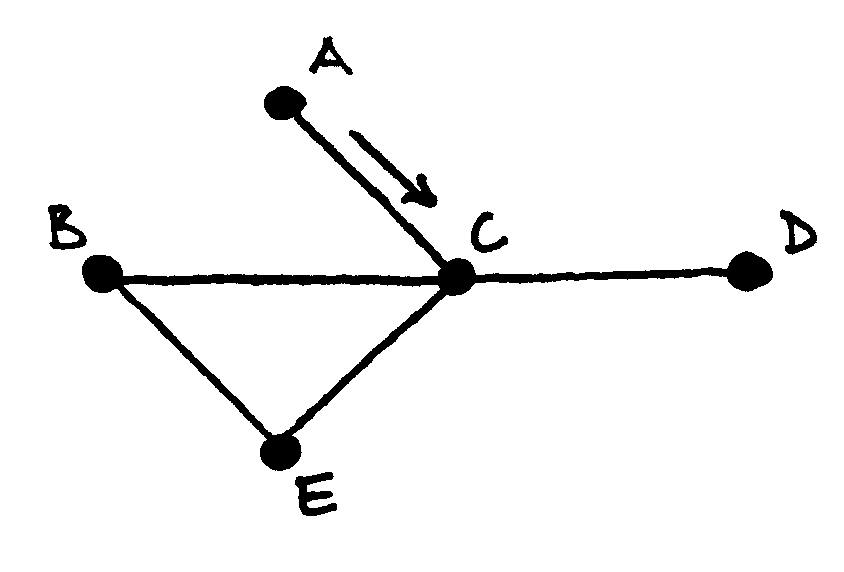
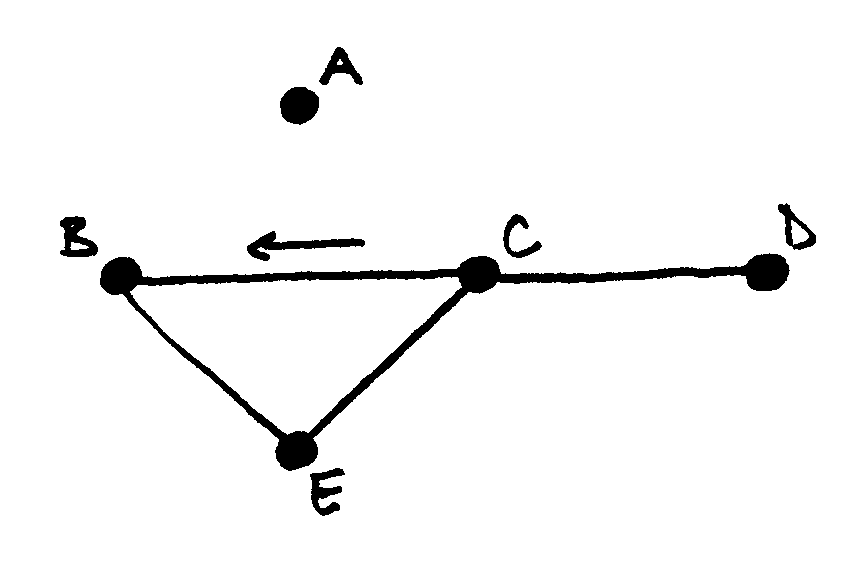
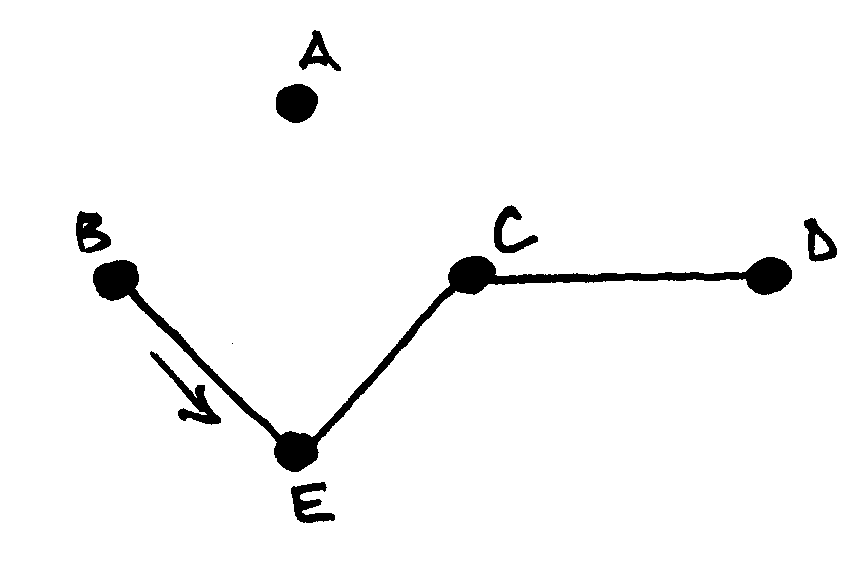
Žinome, kas yra Oilerio kelias ir ciklas, ir netgi mokame duotame grafe nustatyti, ar toks egzistuoja. Tačiau kaip ieškoti Oilerio kelio? Pasirodo, tai labai paprasta. Flerio algoritmas, skirtas Oilerio ciklų ir kelių paieškai, gali būti nusakytas trimis žodžiais: venk eiti tiltu.
Flerio algoritmą, ieškantį Oilerio ciklo, galime išskaidyti į tokius žingsnius:
pradedame bet kurioje viršūnėje;
jei įmanoma, einame briauna, kuri nėra tiltas (jei tokios briaunos nėra, tai einame tiltu);
briauną, kuria jau ėjome, pašaliname iš grafo;
kartojame nuo antro žingsnio, o jei nėra kur eiti, baigiame.
Oilerio kelio paieška skiriasi tik pradinės viršūnės pasirinkimu: pradedame viršūnėje su nelyginiu laipsniu.
Flerio algoritmą Oilerio ciklo arba kelio paieškai multigrafe (t. y. grafe, kuriame dvi viršūnes gali jungti daugiau negu viena briauna) užrašysime programavimo kalba. Multigrafą vaizduosime kaimynystės matrica – kiekvienai porai viršūnių įsiminsime, kelios briaunos jas jungia:
type grafas = record
n : integer;
briaunų_sk : array [1..MAXN,
1..MAXN] of integer;
laipsnis : array [1..MAXN] of integer;
end;
const int MAXN = ...; // maksimalus galimas viršūnių skaičius
// dažniausiai galima nustatyti pagal sąlygoje pateiktus ribojimus
int n; // viršūnių skaičius
int briaunuSk[MAXN][MAXN];
int laipsnis[MAXN];
// Pastaba: pascal kalbos kode grafas pateikiamas kaip struktūra,
// tačiau čia kaimynystės matricą ir laipsnių masyvą apsirašome globaliai.
Tarsime, kad masyvas laipsnis užpildomas sudarant grafą.
Prieš pradedant ieškoti svarbu įsitikinti, ar tenkinamos būtinos ir pakankamos sąlygos. Paprastumo dėlei tarsime, kad grafas jungus, arba jį sudaro tik vienas nevienetinio dydžio jungumo komponentas. Šias sąlygas nesunku patikrinti pasinaudojus paieška gilyn, kaip tai darėme Paieška gilyn skyrelyje.
Viršūnių laipsnių ribojimą patikrinti dar paprasčiau: tereikia suskaičiuoti, kiek viršūnių grafe turi nelyginius laipsnius. Jei tokios bus dvi, tai ieškosime Oilerio kelio ir turėsime pradėti vienoje iš nelyginio laipsnio viršūnių, priešingu atveju galėsime pradėti bet kurioje viršūnėje.
Patikrinus, ar tenkinamos abi sąlygos, galima pradėti vykdyti Flerio algoritmą: įsiminti pradinę viršūnę, pasirinkti tolesnę ir briauną, kuria jau ėjome, išbraukti iš grafo. Tolesnę lankomą viršūnę renkamės pagal minėtą sąlygą – stengiamės neiti tiltu, jei tik įmanoma.
const MAXB = ...; { maksimalus briaunų skaičius }
type masyvas = array [1..MAXB+1] of integer;
procedure Flerio(var g : grafas;
var kelio_ilgis : integer;
var kelias : masyvas);
{ jei Oilerio ciklas/kelias grafe neegzistuoja, tai „kelio_ilgis“
reikšmė lygi nuliui, kitu atveju Oilerio ciklas/kelias įrašomas
į masyvą „kelias“ }
var k, p, v, u, nelyg : integer;
begin
nelyg := 0;
{ suskaičiuojama, kiek yra nelyginio laipsnio
viršūnių, ir parenkama pradinė (v) }
v := 1;
for k := 1 to g.n do
if odd(g.laipsnis[k]) then begin
nelyg := nelyg + 1;
{ jei randama bent viena nelyginio laipsnio viršūnė,
tai v priskiriamas jos numeris }
v := k;
end;
kelio_ilgis := 0;
if ((nelyg = 0) or (nelyg = 2))
{ jei tenkinamos būtinos Oilerio ciklo/kelio egzistavimo sąlygos }
then begin { vykdomas Flerio algoritmas }
while v > 0 do begin
inc(kelio_ilgis);
kelias[kelio_ilgis] := v;
p := v; { paskutinė pereita viršūnė }
v := 0;
{ pagal Flerio algoritmą pasirenkama sekanti viršūnė }
for u := 1 to g.n do
if (g.briaunų_sk[p, u] > 0) and
((v = 0) or not tiltas(g, p, u))
then
v := u;
if v > 0 then begin { ištrinama briauna }
dec(g.briaunų_sk[p, v]);
dec(g.briaunų_sk[v, p]);
end;
end;
end;
end;
const int MAXB = ...; // maksimalus briaunų skaičius
int kelioIlgis;
int kelias[MAXB];
void flerio () {
/*
jei Oilerio ciklas/kelias grafe neegzistuoja, tai "kelioIlgis"
reikšmė bus lygi nuliui, kitu atveju Oilerio ciklas/kelias
įrašomas į masyvą "kelias"
*/
int nelyg = 0;
// suskaičiuojama, kiek yra nelyginio laipsnio viršūnių, ir pradinė viršūnė (v)
int v = 0;
for (int k = 0; k < n; k++) {
if (laipsnis[k] % 2 == 1) {
nelyg++;
v = k;
}
}
kelioIlgis = 0;
if (nelyg == 0 || nelyg == 2) {
/*
jei tenkinamos būtinos Oilerio ciklo/kelio sąlygos,
vykdomas Flerio algoritmas
*/
while (v > -1) {
kelioIlgis++;
kelias[kelioIlgis] = v;
int p = v; // paskutinė pereita viršūnė
v = -1;
// pagal Flerio algoritmą pasirenkama kita viršūnė
for (int u = 0; u < n; u++)
if (briaunuSk[p][u] > 0 && (v == -1 || !tiltas(p, u)))
v = u;
if (v > -1) {
// ištrinama briauna
briaunuSk[p][v]--;
briaunuSk[v][p]--;
}
}
}
}
Liko nerealizuota funkcija tiltas. Ji turėtų grąžinti true
reikšmę, jei grafe 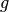 briauna
briauna 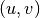 yra tiltas. Tai
patikrinti nesunku: jei
yra tiltas. Tai
patikrinti nesunku: jei 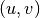 yra tiltas, tai pašalinus šią
briauną viršūnės
yra tiltas, tai pašalinus šią
briauną viršūnės 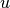 ir
ir  atsidurs skirtinguose
jungumo komponentuose. Taigi pašalinkime šią briauną, paieška gilyn
patikrinkime, ar
atsidurs skirtinguose
jungumo komponentuose. Taigi pašalinkime šią briauną, paieška gilyn
patikrinkime, ar  pasiekiama iš
pasiekiama iš 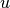 , ir sugrąžinę
pašalintą briauną pateikime rezultatą.
, ir sugrąžinę
pašalintą briauną pateikime rezultatą.
function tiltas(var g : grafas;
u, v : integer) : boolean;
var k : integer;
begin
if g.briaunų_sk[u, v] > 1 then
tiltas := false
else begin
for k := 1 to g.n do
spalva[k] := balta;
g.briaunų_sk[u, v] := 0; { pašalinama briauna }
g.briaunų_sk[v, u] := 0;
ieškok_gilyn (g, u);
{ Ši procedūra pateikta 7.3 skyrelyje, tačiau kitaip
pavaizduotam grafui, taigi prieš taikant ją būtina
modifikuoti. }
g.briaunų_sk[u, v] := 1; { atstatoma briauna }
g.briaunų_sk[v, u] := 1;
tiltas := spalva[v] = balta;
end;
end;
bool tiltas (int v, int u) {
if (briaunuSk[v][u] > 1)
return false;
for (int k = 0; k < n; k++)
spalva[k] = 0;
briaunuSk[v][u]--;
briaunuSk[u][v]--;
dfs(u);
briaunuSk[v][u]++;
briaunuSk[u][v]++;
return spalva[v] == 0;
}
Uždavinys Domino kauliukai 2¶
Yra krūvelė domino kauliukų. Kiekvienas domino kauliukas perskirtas pusiau, kiekvienoje pusėje užrašytas skaičius iš intervalo
. Du kauliukus galima sujungti, jei sutampa skaičiai, užrašyti ant sujungiamų kauliukų pusių.
Užduotis. Reikia nustatyti, ar krūvelėje esančius kauliukus galima sudėlioti į nenutrūkstamą liniją.
Uždavinį modeliuosime grafais. Grafas turės septynias viršūnes, sunumeruotas nuo 0 iki 6 (mat nuo 0 iki 6 taškų gali būti ant domino kauliuko puselės). Kauliukus atitiks grafo briaunos.
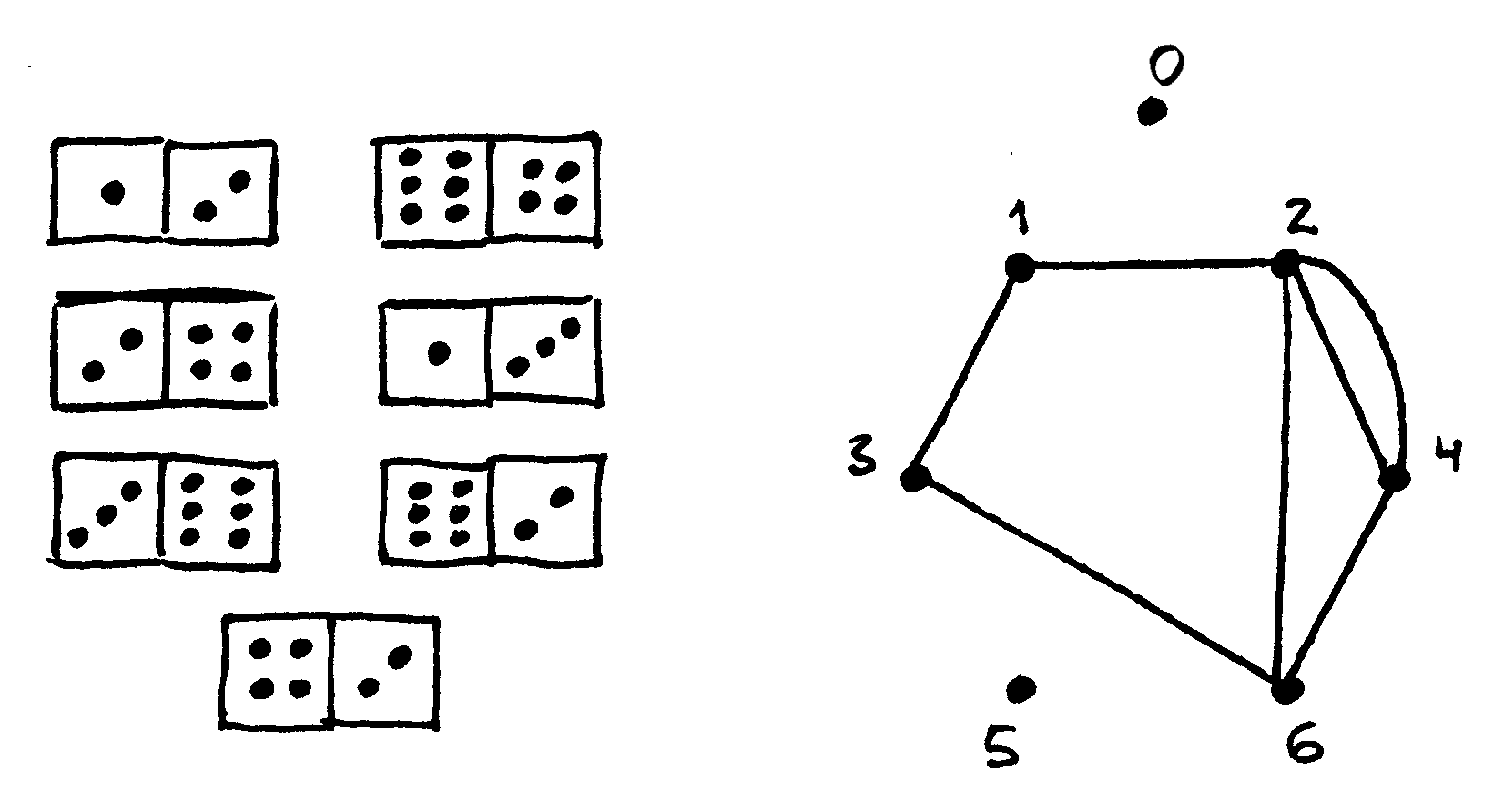
Fig. 48 Kauliukų rinkinys ir juos atitinkantis grafas; grafe Oilerio
kelias yra toks: 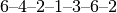 , tad kauliukus galima
sudėlioti į vieną eilę:
, tad kauliukus galima
sudėlioti į vieną eilę: ![[6,4]](_images/math/00a9706e900f915be88e66fc4facbcefcc788368.png)
![[4,2]](_images/math/d1a67abdca3cf37c68f023758b69ad0faa54fc00.png)
![[2,1]](_images/math/f74f37d7dc9788f5b66b9df249b2ce5c104a1788.png)
![[1,3]](_images/math/c1cef7081ce4c49651f50ddfef42cfe5f098ad6b.png)
![[3,6]](_images/math/e026e61670119431d04b097d4a78ce2c4ec855e3.png)
![[6,2]](_images/math/218f10c40b3b9a7f8fb210e4926b8e5933045f3a.png)
![[2,4]](_images/math/9ee224c659df6c62135b7582be9a16a25d3bc560.png) ¶
¶
Kauliukų dėliojimas į liniją atitinka kelią, kai visomis grafo briaunomis apeinama po vieną kartą, t. y. Oilerio kelią. Norint išspręsti šį uždavinį tereikia patikrinti, ar grafe egzistuoja Oilerio kelias.
Hamiltono keliai ir ciklai¶
O brooding Spirit of Wisdom and of Love,Whose mighty wings even now o’ershadow me,Absorb me in thine own immensity,And raise me far my finite self above!Mąslioji išminties ir meilės siela,kurios eiklių sparnų šešėlyje slepiuos,leisk prisiliesti prie gelmės tavosir peržengt savo ribotumo sieną! 3Seras Viljamas Rovanas Hamiltonas (Sir William Rowan Hamilton)

Fig. 49 Seras Viljamas Rovanas Hamiltonas, (Sir William Rowan Hamilton) 1805–1865¶
Airija nėra šalis, kurią garsina matematikai. Tačiau vieną jų – matematiką ir poetą serą Viljamą Rovaną Hamiltoną – žino daugelis. Deja, labai gabaus, daug kalbų žinojusio mokslininko asmeninis gyvenimas buvo nenusisekęs: jis sirgo alkoholizmu ir depresija. 1859 metais – pasakoja, jog pristigęs pinigų – jis sukonstravo ir Dublino žaislų gamintojams pardavė galvosūkį „Aplink pasaulį“ – iš medžio pagamintą taisyklingą dodekaedrą su dvidešimčia viršūnių. Ant kiekvienos viršūnės buvo užrašytas miesto pavadinimas. Tai buvo galvosūkis: reikėjo rasti kelią dodekaedro briaunomis, kuriuo būtų kiekvienas miestas aplankytas po vieną kartą.
Fig. 50 Erdvinis dodekaedro vaizdas¶
Hamiltono keliu imta vadinti kelią, kuriuo einant kiekviena viršūnė aplankoma po vieną kartą.
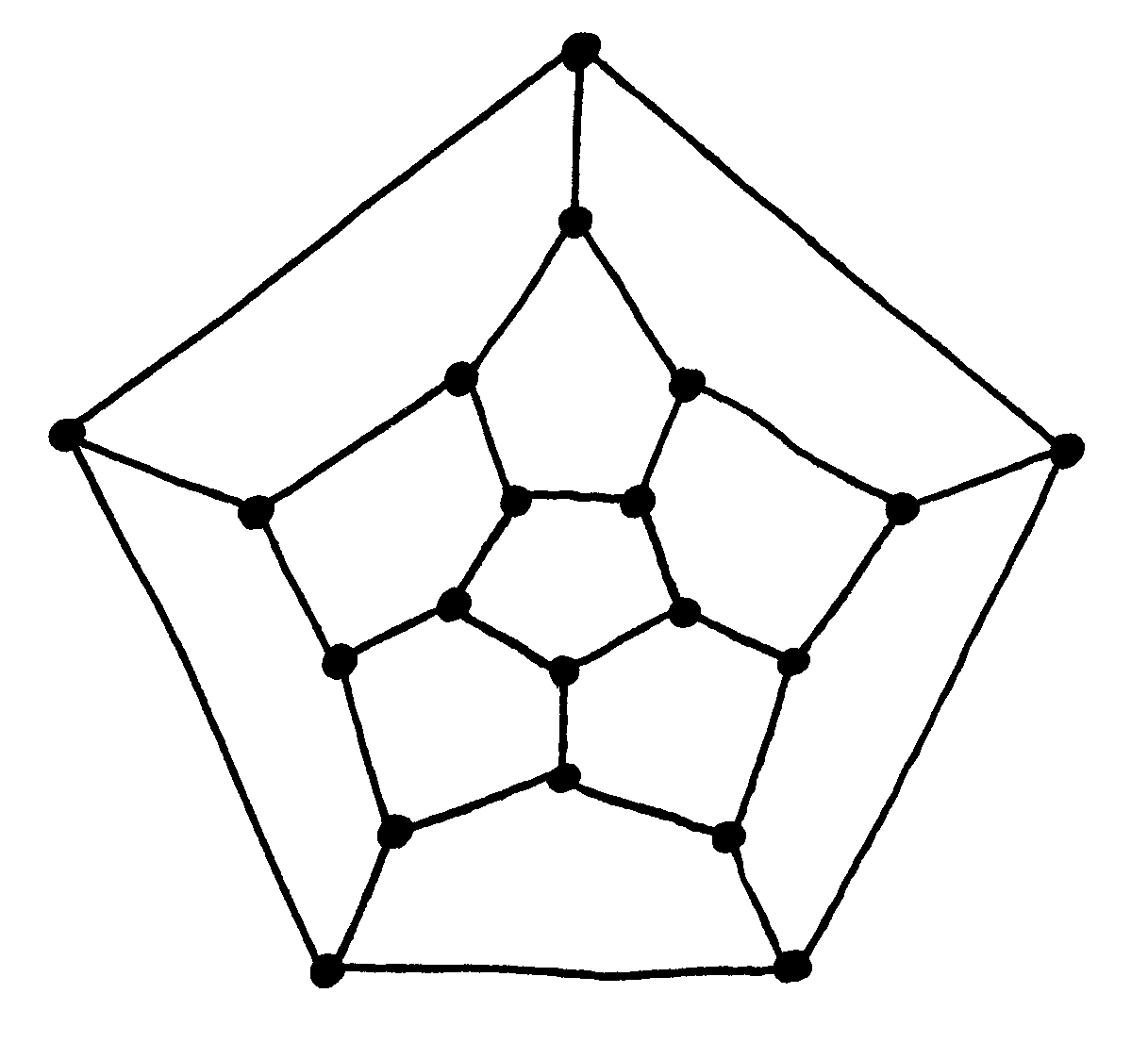
Fig. 51 Dodekaedras, pavaizduotas plokštumoje¶
Atrodytų, Hamiltono kelio uždavinys nedaug skiriasi nuo Oilerio kelio uždavinio: vienu atveju reikia rasti kelią, kuris apeitų visas viršūnes po vieną kartą, kitu atveju – kelią, kuris po vieną kartą apeitų visas briaunas. Tačiau jų sprendimai iš esmės skiriasi. Oilerio ciklus ir kelius sėkmingai randa Flerio algoritmas, o Hamiltono kelio paieška – NP sunkus uždavinys. Tai reiškia, kad nėra žinoma jokio efektyvaus algoritmo šiam uždaviniui spręsti.
Hamiltono kelio paieško uždavinys labai artimas keliaujančio pirklio uždaviniui, su kuriuo jau susidūrėme NP sudėtingumas skyrelyje. Pastarajame uždavinyje grafas yra pilnas (t. y. bet kurios dvi viršūnės yra sujungtos briauna, nes egzistuoja kelias tarp bet kurių dviejų miestų) ir svorinis (grafo briaunoms yra priskirti svoriai, t. y. atstumai tarp miestų).
Hamiltono kelio paieška¶
Ieškodami visų Hamiltono kelių grafe, kurio viršūnės sunumeruotos
nuo 1 iki  , galėtume generuoti visus skaičių nuo 1 iki
, galėtume generuoti visus skaičių nuo 1 iki
 kėlinius (t. y. visas galimas viršūnių apėjimo tvarkas)
kėlinius (t. y. visas galimas viršūnių apėjimo tvarkas)
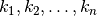 , o sugeneravę patikrinti, ar egzistuoja
visos briaunos
, o sugeneravę patikrinti, ar egzistuoja
visos briaunos 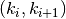 ,
,
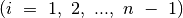 .
.
Tačiau retuose (t. y. tokiuose, kurie turi nedaug briaunų) grafuose
Hamiltono kelių galima ieškoti kur kas efektyviau. Viršūnių seką
galima iškart sudaryti taip, kad gretimas sekos viršūnes jungtų
briauna. Naudodami grįžimo metodą parašysime procedūrą,
spausdinančią visus konkrečioje viršūnėje  prasidedančius Hamiltono kelius. Grafą vaizduosime kaimynystės
sąrašais.
prasidedančius Hamiltono kelius. Grafą vaizduosime kaimynystės
sąrašais.
const MAXN = ...;
var seka : array [1..MAXN] of integer;
aplankyta : array [1..MAXN] of boolean;
procedure ieškok(var g : grafas;
k, { kiek viršūnių apeita }
v : integer { kurioje viršūnėje sustota } );
var i, u : integer;
begin
seka[k] := v;
{ aplankytomis žymimos konstruojamame kelyje esančios viršūnės }
aplankyta[v] := true;
if (k = g.n) then
{ jei apeitos visos viršūnės – tai rastas Hamiltono kelias}
spausdink (g.n)
{ Procedūra spausdink(m) išveda masyvo elementus nuo 1 iki
m; ji analogiška 5.1 skyrelyje pateiktai procedūrai. }
else
{ bandoma toliau eiti į visas neaplankytas v kaimynes }
for i := 1 to g.vir[v].k do begin
u := g.vir[v].ksąrašas[i];
if (not aplankyta[u]) then
ieškok(g, k + 1, u);
end;
{ pabaigus, v pažymima kaip neaplankyta }
aplankyta[v] := false;
end;
const int MAXN = ...;
int seka[MAXN];
bool aplankyta[MAXN];
void ieskok (int k, int v) {
/*
k - kiek viršūnių apeita,
v - kurioje viršūnėje sustota
*/
seka[k] = v;
// aplankytomis žymimos konstruojamame kelyje esančios viršūnės
aplankyta[v] = true;
if (k == n) {
// jei apeitos visos viršūnės - tai rastas Hamiltono kelias
spausdink(n);
} else {
// bandoma toliau eiti į visas neaplankytas v kaimynes
for (int u : adj[v])
if (!aplankyta[u])
ieskok (k+1, u);
}
aplankyta[v] = false;
}
Norint rasti Hamiltono kelius, prasidedančius visose viršūnėse, reikia įvykdyti:
for v := 1 to g.n do
ieškok(g, 1, v);
for (int v = 0; v < n; v++)
ieskok (1, v);
Jei ieškotume ne kelių, o ciklų, tuomet sugeneravus visą seką reiktų papildomai patikrinti, ar egzistuoja briauna, jungianti pirmą ir paskutinę kelyje esančias viršūnes.
Išnašos